Магнитное поле

Мы переходим к описанию магнитного поля, считая магнетизм релятивистским эффектом. Однако, исторически, представления о магнитном поле возникли ранее представлений об электрическом поле. Его практическое использование началось гораздо раньше после изобретения компаса. Еще в 1600 г. Гильберт объяснил магнетизм Земли (W.Gilbert, De magnete, magneticiscue corporibus, et mango magnete tellure, 1600), представив ее большим намагниченным шаром. Для этого он изучил магнитное поле шара из магнитной руды. На его рисунках приведены направления стрелок инклинатора (компас, в котором ось вращения стрелки направлена горизонтально), которые можем считать картинками визуализации магнитного поля постоянного магнита. Начиная с работ Эрстеда, Ампера, Фарадея магнитное поле связывается с движущимися зарядами, а затем Максвелл определяет электромагнитное поле.

§ 14 Магнитное поле

Определение магнитного поля (12.2) в виде ротора векторного поля 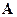приводит нас к тому, что магнитное поле – вихревое поле, поскольку поле 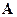– аксиальное поле. С этой связью вихревого и аксиального полей мы уже имели дело при решении задачи обтекания шара медленным вязким потоком (Механика, §26).

Кроме дифференциального соотношения (12.2) отметим интегральную связь между векторными полям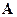и и 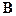, которая вытекает из теоремы Стокса:

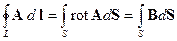(14.1)

- поток вектора 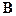через произвольную площадку 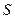равен циркуляции вектора 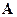по замкнутому контуру, ограничивающему эту площадку. Отметим также, что поскольку дивергенция всякого ротора равна нулю, для дивергенции магнитного поля получаем

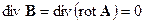. (14.2)

Это уравнение является отражением экспериментально установленного отсутствия магнитных “зарядов” – монополей в природе.

Вы хорошо помните из школьного курса физики картинки, полученные при визуализации магнитного поля с помощью железных опилок – вытянутых постоянных магнитов. Они ориентировались параллельно силовым линиям поля, их было больше там, где была больше величина поля. Благодаря этим картинкам магнитное поле получалось почти осязаемым, почти реальным объектом природы. Однако магнитное поле это только удобная модель, реальны же фотоны – частицы, переносящие электромагнитное взаимодействие. Если забежать вперед и рассмотреть дифракцию электронов на двух щелях в присутствии постоянного магнита – нитевидного кристалла ферромагнетика, то можно наблюдать сдвиг дифракционной картины. Сплошная кривая – дифракционная картина без постоянного магнита, пунктирная – с постоянным магнитом, сечение которого заштриховано на рис. 14.1.

Рис.14.1

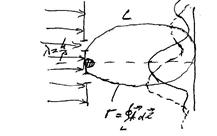
Длинный нитевидный кристалл – аналог длинного соленоида, магнитное поле есть только внутри него, в окружающем пространстве магнитного поля нет. С другой стороны в окружающем пространстве есть векторное поле 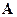, циркуляция которого по контуру 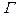, в соответствии с уравнением 14.1, не равна нулю. С точки зрения анализа этого эксперимента более реальным объектом является векторное поле 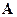, а не магнитное поле, поскольку в других экспериментах сила Лоренца действует на движущийся заряд и без определения магнитного поля. Здесь же, если ограничиваться только представлением о магнитном поле, то объяснить сдвиг дифракционной картины невозможно.

§ 15 Эксперименты по поиску монополей

Если мы из куска проволоки сделаем постоянный магнит, то он будет диполем, у него будет северный и южный полюса. Разрезая проволоку на два кусочка, получим два магнита, каждый из которых опять будет диполем. Получить после подобного разделения диполя кусочек с отдельным северным полюсом – “северный магнитный монополь” и отдельным южным - “южный магнитный монополь” еще никому не удавалось.

Хотя асимметрия электрического и магнитного полей в классической электродинамике очевидна – она основана на СТО, поиски магнитных монополей были стимулированы П.Дираком. Он предложил (1931 г.) квантово-механическую теорию, описывающую движение магнитного монополя в электрическом поле и электрического заряда в поле магнитного монополя. Из нее вытекала необходимость квантования электрического и магнитного зарядов. Поскольку нам известно, что электрический заряд квантуется, притягательность теории Дирака была в том, что она единственная обосновывала квантование заряда. Теория Дирака позволяла оценить элементарный магнитный заряд и, соответственно, энергию частиц им обладающим. Для элементарного электрического заряда 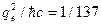, для элементарного магнитного заряда 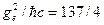. Что необходимо было искать, экспериментаторы знали. Однако ни в одной камере Вильсона, ни в одной пузырьковой камере не было обнаружено магнитных монополей.

С изобретением SQUID (Superconducting Quantum Interference Detector) – сверхпроводящего квантового интерферометра появилась еще одна возможность регистрировать магнитные монополи. О квантовании магнитного потока и принципах работы SQUID поговорим позднее, здесь же отметим, что и в этих экспериментах магнитных монополей не обнаружено.

Новый интерес к поиску магнитных монополей, правда, с совершенно другими свойствами, появился после создания полевых теорий пытающихся объединить все фундаментальные взаимодействия (1974, Поляков, Хоофт). Масса магнитного монополя, предсказываемая этой теорией гигантская 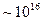ГэВ. Предполагается, что они могли образоваться на раннем этапе развития Вселенной. Однако, ни одним из имеющихся в распоряжении экспериментаторов детектором (в том числе и теми, которые регистрируют солнечные нейтрино), такие магнитные монополи космического происхождения зарегистрированы не были.

Отрицательный экспериментальный результат это тоже результат, заслуживающий внимания. То, что магнитные монополи не обнаружены, “спасает” специальную теорию относительности: нет необходимости отказываться от 4-потенциала. Мы можем продолжать считать магнетизм исключительно релятивистским эффектом.

§ 16 Магнитное поле проводников с токами

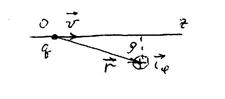
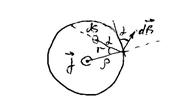
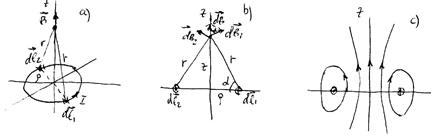
Магнитное поле в произвольной точке, созданное одним движущимся зарядом 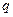, лучше всего определить в цилиндрических координатах (рис.16.1), совмещая ось z с направлением движения заряда. Рассмотрим заряд в тот момент времени, когда он находится в начале системы координат.

Рис.16.1

Векторный потенциал в этом случае равен:

.

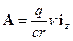Магнитное поле, в свою очередь будет равно:

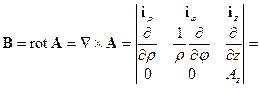
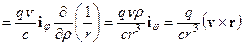. (16.1)

Мы здесь использовали оператор Гамильтона в цилиндрических координатах 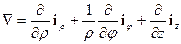, а также вытекающее из условия 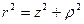равенство 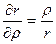. Окончательный результат выражен через векторное произведение .

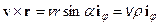Если в начале координат находится кусок проводника с током 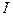, характеризуемый вектором 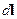, то магнитное поле, созданное этим током будет равно (закон Био-Савара):

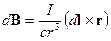. (16.2)

Пользуясь этим результатом, можем найти магнитное поле вблизи некоторых симметричных проводников с токами. Для этого интегрируем выражение (16.2) по всей длине проводника.

1. Для прямого длинного проводника с током (рис.16.2а) магнитное поле на удалении 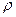от него будет равно:

. (16.3)

Рис.16.2

При вычислении интеграла мы использовали уравнения связывающие переменные: 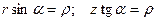. Для указанных пределов интегрирования мы движемся вдоль проводника из 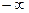в 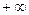. Силовые линии получившегося магнитного поля – концентрические окружности (рис.16.2b).

2. Магнитное поле на поверхности длинного прямого цилиндрического проводника радиуса 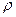с током постоянной плотности 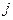(рис.16.3).

Рис.16.3

Результирующее поле в любой точке на поверхности будет направлено по касательной, поэтому прежде чем интегрировать магнитное поле, созданное током через произвольную площадку 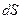, вектор 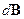нужно спроектировать на направление касательной 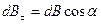. После интегрирования по всему сечению проводника получим:

.

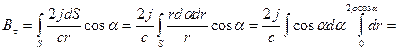
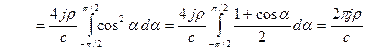Поскольку произведение 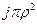равно силе тока в проводнике, магнитное поле на поверхности проводника будет определяться выражением (16.3). Поле вне проводника также будет определяться этим выражением.

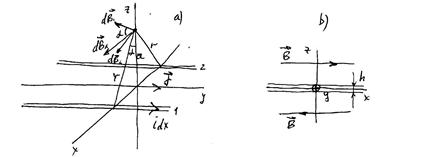
3. Магнитное поле плоского листа с током. Пусть линейная плотность тока 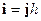, где 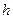- толщина листа с током, а вектор плотности тока 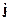параллелен оси y (рис.16.4а). Тогда искомое поле может быть найдено интегрированием магнитного поля полоски с током 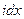. На рисунке видно, что для двух симметрично расположенных полосок 1 и 2 проекции магнитного поля на ось z компенсируют друг друга. Поэтому результирующее поле будет направлено вдоль оси x, и мы вычисляем

Рис.16.4

интеграл для проекции:

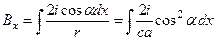
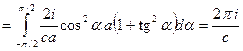. (16.4)

При замене переменных мы пользовались уравнениями связи 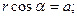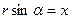. Для безграничного листа с током получили однородное магнитное поле во всем пространстве, силовые линии которого показаны на рис.16.4b. Естественно, что для проводников конечных размеров, полученный результат будет справедлив вдали от краев на небольшом удалении от плоскости проводника.

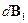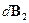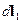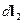4. Магнитное поле на оси кругового витка с током. Если рассмотреть магнитные поля и (рис.16.5a,b), созданные токами в кусках кругового витка и , которые расположены диаметрально противоположно, то видно, что результирующее поле будет направлено по оси z.

Интегрируя, для 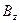проекции в точке на оси z кольца с током получим:

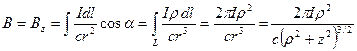. (16.5)

Рис.16.5

Магнитное поле кругового витка с током иллюстрирует рис 16.5c. Силовая линия на оси витка приходит из 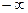и уходит в 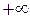. Видно, что это поле очень неоднородно. Однако, используя два витка (на практике две катушки с N витками) разнесенных по оси z на расстояние примерно равное радиусу витка, можно получить почти однородное магнитное поле в пространстве между витками вблизи оси. Витки (катушки) соединяются последовательно, в них течет одинаковый ток. Подобное устройство называется катушками Гельмгольца.

5. Магнитное поле соленоида. Для получения более сильного однородного магнитного поля, чем у катушек Гельмгольца, используют соленоид – катушку, равномерно намотанную на цилиндрическую поверхность (рис.16.6a,b). Зная параметры соленоида - радиус цилиндрической поверхности, 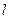- длину соленоида, 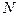- число витков, можем определить число витков на единицу длины 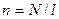при равномерной намотке катушки. Тогда в слое соленоида толщиной 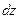оказывается 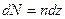витков.

Рис.16.6

Магнитное поле, созданное токами в витках этого слоя 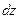в произвольной точке на оси с координатой 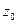внутри соленоида будет равно:

.

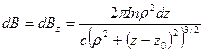Поле в этой точке, созданное всем соленоидом с током 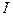, получим после интегрирования по всей длине соленоида:

.

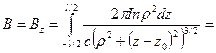
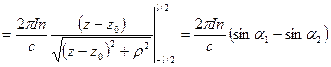В частности, для бесконечно длинного соленоида, угол 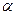меняется от 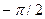до 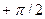. Магнитное поле внутри него будет однородным и равным

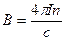. (16.6)

Вне соленоида будет слабое поле, совпадающее с магнитным полем прямого проводника с током (16.3), поскольку вдоль соленоида течет ток 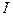. Обмотка соленоида – спираль, пусть с малым, но конечным, равным диаметру проволоки, шагом.

§ 17 Циркуляция магнитного поля

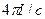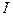Для всех проводников с токами, которые мы рассмотрели в предыдущем параграфе, циркуляция магнитного поля по любому замкнутому контуру равна , где - ток, протекающий через площадку, ограниченную контуром.

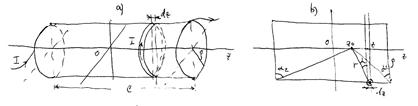
Покажем это на примере длинного прямого проводника с током. Циркуляция по контуру 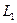(рис.17.1) будет равна:

.

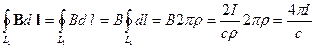В этом случае контур охватывает проводник с током.

Рис.17.1

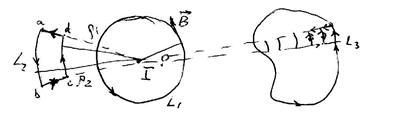
Циркуляция по контуру будет равна:

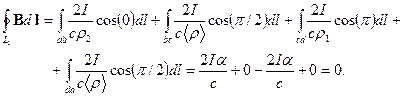
В этом случае контур (специальной формы) не охватывает проводника с током. Этот результат можно обобщить на контур произвольной формы. Поскольку циркуляция аддитивна (Механика, §22), то циркуляция по контуру 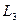будет равна сумме циркуляций по маленьким контурам. Их форма может совпадать с формой контура 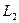. Контур 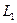мы также можем взять произвольной формы, представив его в виде набора элементов двух типов: элементы, направленные по радиусу (для них вклад в циркуляцию равен нулю также как и для элементов ad и bc контура 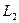) и элементы, представляющие собой куски окружностей разного радиуса. Более того, результат не изменится, если замкнутый контур не будет лежать в плоскости, перпендикулярной проводнику.

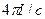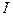Мы можем обобщить полученный результат следующим образом: циркуляция магнитного поля по произвольному замкнутому контуру будет равна , где - ток, протекающий через площадку, ограниченную контуром. В силу принципа суперпозиции полей можно утверждать, что для нескольких проводников с токами

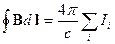, (17.1)

где суммирование ведется по всем проводникам, которые охватывает контур интегрирования. Если циркуляция вычисляется по контуру в проводящей среде с током, характеризуемым в каждой точке вектором 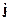, то сумма справа в (17.1) перейдет в интеграл

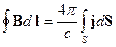, (17.2)

который вычисляется по площадке, ограниченной замкнутым контуром.

Используя теорему Стокса, можно от интегрального соотношения (17.2) перейти к дифференциальному соотношению между магнитным полем 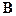и током 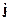его порождающим:

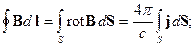
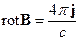. (17.3)

Получили знакомый нам из гидродинамики результат: ротор аксиального поля дает нам вихревое поле, ротор которого нам опять дает аксиальное поле (Механика, §26, решение задачи Стокса):

.

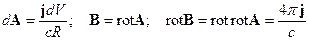Можно доказать справедливость дифференциального соотношения (17.3) исходя из общих определений, воспользовавшись векторным анализом.

Все магнитные поля для симметричных проводников с токами, которые мы рассмотрели в §16, могут быть получены с помощью уравнения (17.2), которое называют теоремой о циркуляции магнитного поля.

§ 18 Сила Ампера

Если проводник с током находится в магнитном поле, то на каждый носитель заряда, движущийся с дрейфовой скоростью 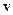, будет действовать магнитная составляющая силы Лоренца (12.4). Ее часто называют просто силой Лоренца. Выделим элемент проводника с током 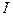, который характеризуется вектором 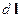(рис.18.1).

Рис.18.1

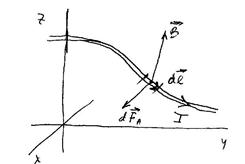
Количество свободных носителей заряда в нем 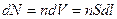. Сила, действующая на каждый носитель заряда, передается атомам проводника (хотя носители и свободные, но не настолько, чтобы совсем не взаимодействовать с атомами). Результирующая сила, действующая на элемент с током 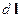, будет равна:

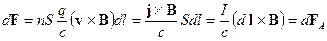. (18.1)

Она называется силой Ампера (H.Ampere), который первым описал взаимодействие проводников с токами и силу, действующую на проводник с током в магнитном поле. Формула (18.1) весьма условна, как и все формулы, в которые входит вектор элемента с током 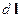, поскольку создать такой объект невозможно. Здравый смысл возвращается, как только мы определяем результирующую силу, действующую на весь проводник с током:

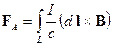. (18.2)

Применим этот результат для нескольких частных случаев, которые будут важны для нас в дальнейшем.

1. Круговой виток с током 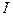в однородном магнитном поле 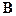. Если магнитное поле направлено перпендикулярно плоскости витка, пусть для определенности 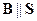(рис.18.2а), то результирующая сила Ампера, как и суммарный момент сил Ампера, будут равны нулю. Положительное направление вектора 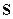выбираем таким, чтобы, глядя с этого направления, ток в контуре был направлен против часовой стрелки.

Действие силы Ампера приведет к натяжению витка. Условие равновесия элемента 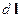: 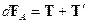. Проекция этого векторного равенства на направление биссектрисы угла даст нам следующее уравнение:

.

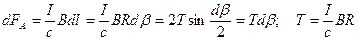Мы учли, что силы натяжения в каждом сечении витка одинаковы. В витке

Рис.18.2

появилось упругое напряжение:

,

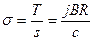где 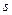- площадь сечения проводника, 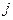- плотность тока в нем.

Теперь рассмотрим произвольную ориентацию витка с током. Пусть угол между векторам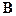и и 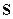равен 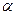(рис.18.2b). В этом случае результирующая сила Ампера, действующая на контур, будет опять же равна нулю, а момент сил Ампера будет направлен по оси х и его модуль будет равен:

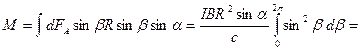
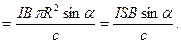
Определим магнитный момент 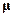плоского контура с током:

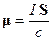. (18.3)

Тогда момент сил Ампера, действующий на плоский контур будет равен:

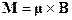. (18.4)

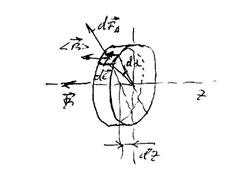
2. Соленоид радиуса 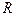с током 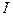и числом витков на единицу длины 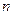. Магнитное поле вне соленоида пренебрежимо мало, внутри соленоида поле определяется выражением (16.6). Можем считать, что эффективное поле, в котором находится оболочка соленоида с током, равно половине поля в соленоиде: 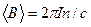. На рис.18.3 показана часть длинного соленоида толщины .

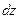Рис.18.3

Сила Ампера, действующая на площадку 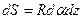, будет равна:

.

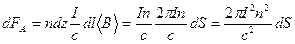Можем определить давление, стремящееся разорвать проводящую оболочку соленоида:

.

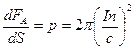В этом случае соленоид с током не находится во внешнем поле, однако появляются силы Ампера, стремящиеся разорвать оболочку соленоида. Учет давления на оболочку, которое мы определили, будет определяющим при проектировании импульсных устройств для получения больших магнитных полей.

§ 19 Переменное магнитное поле. Электромагнитная индукция

Из общего определения электрического поля (12.3), вычислив ротор левой и правой части, получим:

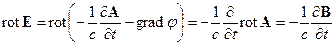, (19.1)

поскольку ротор всякого градиента равен нулю. Видно, что переменное во времени магнитное поле порождает вихревое электрическое поле.

Подкрепим этот результат, рассмотрев несколько частных задач.

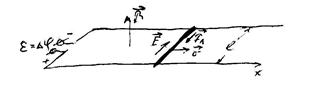
1. Рассмотрим контур, площадь которого меняется в однородном магнитном поле 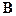. Магнитное поле направлено перпендикулярно плоскости, в которой лежит контур. Одна из перемычек движется с постоянной скоростью 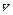, ее длина 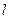(рис.19.1). Если контур разомкнут, то, как принято говорить, в нем появится электодвижущая сила (ЭДС) .

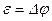Рис.19.1

На свободные носители заряда в движущейся перемычке будет действовать магнитная составляющая силы Лоренца (12.4). Заряды начнут перераспределяться, появится электрическое поле, в равновесном состоянии такое, что 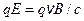. На концах перемычки будет разность потенциалов 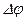, равная 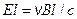. Потенциал неподвижных частей контура одинаков, поэтому мы можем сказать, что в контуре появится ЭДС, равная 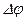. Циркуляция вектора напряженности электрического поля по контуру и будет равна этой разности потенциала (4.5):

.

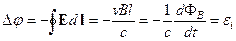Направление обхода контура выбираем против часовой стрелки, если смотреть с конца вектора .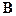

Формально полученный знак минус отражает правило Ленца: для замкнутого контура индукционный ток направлен так, чтобы магнитное поле, создающееся индукционным током, препятствовало бы изменению магнитного потока, пронизывающего контур. При установлении правила Ленца необходимо помнить, что силой, заставляющей заряды в контуре двигаться, будет магнитная составляющая силы Лоренца. Правило Ленца является частным случаем, применимым в электродинамике, более общего принципа Ле-Шателье: всякое внешнее воздействие, выводящее систему из равновесного состояния, генерирует в системе процессы, стремящиеся уменьшить влияние внешнего воздействия. Это некий глобальный принцип отрицательной обратной связи. Правило Ленца мы обосновали строго, а оно было отправной точкой при формулировании принципа Ле-Шателье, к которому мы еще вернемся в термодинамике.

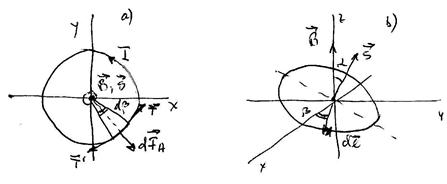
2. Контур, вращающийся в постоянном однородном магнитном поле 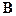(рис.19.2). Устройство, которое мы сейчас рассмотрим, может быть использовано в качестве генератора переменного напряжения, меняющегося по гармоническому закону с частотой, равной частоте вращения контура.

Контур – круговой виток радиуса 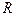, вращается с угловой скоростью 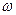. На рис.19.2 показан общий вид a), проекция на плоскость перпендикулярную оси вращения b), проекция на плоскость контура с). В произвольный момент времени угол между вектором 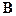и вектором площадки контура 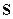равен 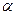. Тогда в куске контура 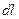появится сила Лоренца, действующая на свободные носители. Если контур разомкнут, эта сила уравновесится кулоновской силой так, что

.

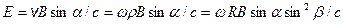Рис.19.2

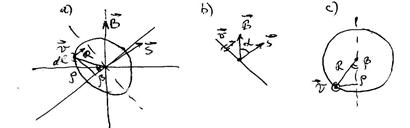
Циркуляция электрического поля по всей длине кольца равна:

.

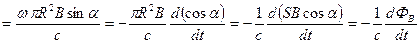И в этом случае получили ЭДС, возникающую в контуре, пропорциональную скорости изменения магнитного потока, пронизывающего площадку, ограниченную контуром.

3. Неподвижный неизменный контур в переменном магнитном поле. М.Фарадей, изучая открытое им явление электромагнитной индукции, экспериментально проанализировал всевозможные способы получения индукционного тока в контуре. При анализе электромагнитной индукции переход от индукционных токов, которые сложнее описать, к ЭДС сделал Максвелл. Неважно за счет чего меняется во времени магнитный поток, пронизывающий контур, всегда возникающая при этом в нем ЭДС оказывается равна:

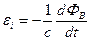. (19.2)

Это выражение называют законом электромагнитной индукции Фарадея. В случае переменного магнитного поля и неподвижного неизменного контура

.

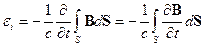Частная производная по времени использовалась потому, что все остальные параметры постоянны. Этот случай говорит нам о том, что с переменным магнитным полем связано вихревое (переменное же в общем случае) электрическое поле. Интегральная связь между ними:

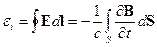. (19.3)

Связь в дифференциальной форме, вытекающая из определения электрического поля, дается уравнением (19.1). Это же уравнение может быть получено из (19.3) после использования теоремы Стокса:

.

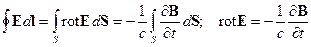Резюме: переменное магнитное поле порождает вихревое электрическое поле.

§ 20 Индуктивность проводников

Если произвольный контур подключить к источнику с ЭДС 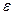, то ток в нем мгновенно появиться не сможет. Это связано с тем, что ток в контуре создает магнитное поле. Раз ток меняется во времени, магнитный поток, сцепленный с этим контуром, также будет меняться. Как следствие закона электромагнитной индукции, в контуре появится ЭДС индукции 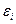, препятствующая возрастанию тока:

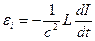, (20.1)

где 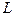- индуктивность контура. Знак минус отражает правило Ленца.

Со временем в контуре установится стационарный ток 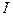. В окружающем пространстве будет стационарное магнитное поле, сцепленное с контуром. Использование определения сцепленное связано с тем, что магнитное поле – вихревое, все силовые линии замкнутые и пронизывают площадку, ограниченную контуром. Силовые линии как кольца нанизаны на виток. Для кругового витка с током вышесказанное иллюстрирует рис.16.5с.

Между магнитным потоком через площадку, ограниченную контуром, и силой тока в нем есть линейная зависимость (считаем пока, что контур с током находится в вакууме):

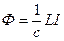. (20.2)

Используя это выражение, можем найти индуктивность некоторых симметричных контуров.

1. Индуктивность единицы длины соленоида. Магнитный поток, сцепленный с куском соленоида длиной 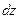(рис.18.3) равен:

.

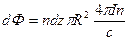Индуктивность единицы длины безграничного соленоида равна:

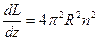. (20.3)

2. Индуктивность тороидальной катушки квадратного сечения. Внутренний радиус 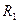, внешний радиус 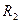, толщина 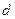, число витков 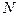(рис.20.1а).

Рис.20.1

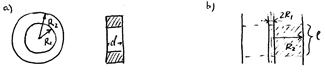
Магнитный поток через сечение катушки равен:

.

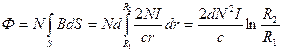При вычислениях мы использовали значение магнитного поля на произвольном удалении от оси, которое нашли с помощью теоремы о циркуляции магнитного поля:

.

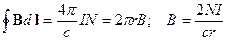Для индуктивности тороидальной катушки с прямоугольным сечением получили следующий результат:

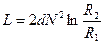. (20.4)

3. Индуктивность единицы длины коаксиального кабеля, радиус сечения центрального проводника которого 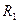, а радиус внешней цилиндрической проводящей оболочки 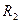(рис.20.1b).

Магнитный поток, пронизывающий заштрихованную на рисунке площадку, равен

,

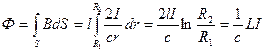а индуктивность единицы длины кабеля равна

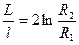. (20.5)

Такие параметры кабеля, как емкость и индуктивность единицы длины мы в дальнейшем будем использовать для определения его волнового сопротивления, которое, в свою очередь, будет использоваться для согласования линии связи (коаксиальный кабель) и нагрузки.

§ 21 Энергия магнитного поля

Определим работу источника тока, которую он должен совершить, чтобы в контуре с индуктивностью 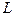создать ток 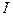. Работа источника, по перемещению заряда 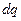против ЭДС индукции равна: 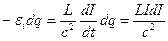. Она же равна увеличению энергии магнитного поля контура при увеличении в нем тока на 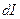. Полную энергию магнитного поля контура с током 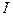получим после интегрирования:

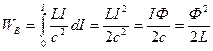. (21.1)

В частности, энергия магнитного поля в куске безграничного соленоида длиной 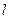будет равна:

.

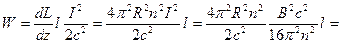
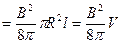В преобразованиях мы использовали результаты 20.3 и 16.6. Окончательный результат дает нам энергию однородного магнитного поля в объеме 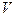. Используя его, можем определить объемную плотность энергии магнитного поля:

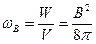. (21.2)

В случае неоднородного магнитного поля его энергия в любом объеме может быть найдена интегрированием по этому объему:

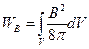. (21.3)

Энергетические соотношения могут быть использованы и для нахождения индуктивностей проводников. Покажем это на третьем примере, рассмотренном в предыдущем параграфе.

Определяем энергию магнитного поля на единицу длины коаксиального кабеля, а затем и индуктивность единицы длины:

.

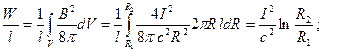
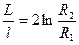Получили тот же результат, что и при использовании для вывода выражения (20.2).