Согласно статистическому толкованию волновой функции 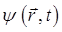 знание этой функции для определённого момента времени
знание этой функции для определённого момента времени 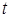 позволяет указать вероятность нахождения частицы в элементе объёма
позволяет указать вероятность нахождения частицы в элементе объёма 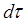 в этот момент времени
в этот момент времени 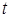 . Наглядное представление можно при этом осуществить, воспользовавшись «картиной распределения», которая строится следующим образом. Представим себе большое число
. Наглядное представление можно при этом осуществить, воспользовавшись «картиной распределения», которая строится следующим образом. Представим себе большое число 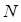 частиц, которые все находятся в одном и том же состоянии в момент времени
частиц, которые все находятся в одном и том же состоянии в момент времени 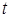 и между собой не взаимодействуют. Так как
и между собой не взаимодействуют. Так как 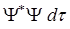 есть вероятность нахождения частицы в объёме
есть вероятность нахождения частицы в объёме 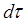 , то
, то 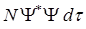 будет очевидно средним числом частиц в объёме
будет очевидно средним числом частиц в объёме 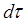 , расположенном около определённой точки пространства, а
, расположенном около определённой точки пространства, а 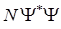 средней плотностью частиц в этой точке. Вычислив эту среднюю плотность для достаточно большого числа точек, мы можем при помощи какого-либо геометрического образа, например в виде облака большей или меньшей густоты, построить картину распределения плотности для данного момента времени
средней плотностью частиц в этой точке. Вычислив эту среднюю плотность для достаточно большого числа точек, мы можем при помощи какого-либо геометрического образа, например в виде облака большей или меньшей густоты, построить картину распределения плотности для данного момента времени 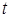 . Если при этом частицы несут электрический заряд
. Если при этом частицы несут электрический заряд 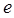 , то произведение
, то произведение 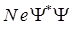 будет средней плотностью заряда в данном месте, и мы можем построить также картину среднего распределения плотности электричества. Значение общего уравнения Шрёдингера с этой точки зрения состоит в том, что оно позволяет найти зависимость волновой функции
будет средней плотностью заряда в данном месте, и мы можем построить также картину среднего распределения плотности электричества. Значение общего уравнения Шрёдингера с этой точки зрения состоит в том, что оно позволяет найти зависимость волновой функции 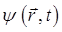 от времени, а зная эту зависимость, можно будет предсказать картину распределения электронной плотности во все последующие моменты времени и, таким образом, следить за изменениями, происходящими в рассматриваемой квантово-механической системе. Однако этот способ едва ли может вполне удовлетворить нашему желанию получить полную картину движения. Мы приблизимся к этой цели в большей степени, если сможем указать наряду с распределением частиц или с распределением плотности заряда также и среднее число частиц, проходящих в 1 с через площадку в 1 см2 в направлении положительной нормали к площадке. Для этой цели произведение
от времени, а зная эту зависимость, можно будет предсказать картину распределения электронной плотности во все последующие моменты времени и, таким образом, следить за изменениями, происходящими в рассматриваемой квантово-механической системе. Однако этот способ едва ли может вполне удовлетворить нашему желанию получить полную картину движения. Мы приблизимся к этой цели в большей степени, если сможем указать наряду с распределением частиц или с распределением плотности заряда также и среднее число частиц, проходящих в 1 с через площадку в 1 см2 в направлении положительной нормали к площадке. Для этой цели произведение 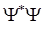 оказывается уже непригодным, и нужно поискать другую комбинацию тех же функций, подходящую для этого назначения. Эту комбинацию мы отыщем, если примем во внимание, что поскольку
оказывается уже непригодным, и нужно поискать другую комбинацию тех же функций, подходящую для этого назначения. Эту комбинацию мы отыщем, если примем во внимание, что поскольку 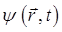 есть непрерывная функция координат, то
есть непрерывная функция координат, то 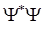 можно уподобить некоторой фиктивной жидкости, разлитой во всём пространстве. Эта «жидкость» в общем случае подчиняется некоторому закону сохранения. В самом деле, интеграл вида:
можно уподобить некоторой фиктивной жидкости, разлитой во всём пространстве. Эта «жидкость» в общем случае подчиняется некоторому закону сохранения. В самом деле, интеграл вида:
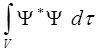
взятый по всему фазовому пространству, от времени не зависит. Поэтому, если в определённый момент времени плотность вероятности 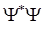 где-нибудь возрастает, то в другом месте она соответственно убывает, то есть можно себе представить, что вероятность как бы «течёт». Принимая во внимание это, мы можем использовать для вывода интересующего нас выражения плотности тока вероятности аналогию с уравнением непрерывности классической электродинамики. Как известно, сила тока равняется потоку вектора
где-нибудь возрастает, то в другом месте она соответственно убывает, то есть можно себе представить, что вероятность как бы «течёт». Принимая во внимание это, мы можем использовать для вывода интересующего нас выражения плотности тока вероятности аналогию с уравнением непрерывности классической электродинамики. Как известно, сила тока равняется потоку вектора 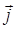 через поверхность поперечного сечения проводника:
через поверхность поперечного сечения проводника:
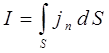
Для электрического тока остаётся справедливым закон сохранения заряда. Установим взаимосвязь между объёмной плотностью заряда и вектором плотности тока 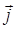 . Для этого условно выделим в проводнике произвольный объём V, ограниченный замкнутой поверхностью S. Пусть в выделенном объёме V содержится заряд
. Для этого условно выделим в проводнике произвольный объём V, ограниченный замкнутой поверхностью S. Пусть в выделенном объёме V содержится заряд 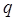 , распределённый с объёмной плотностью
, распределённый с объёмной плотностью 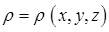 . Так, если из объёма V сквозь поверхность S вытекает позитивный заряд
. Так, если из объёма V сквозь поверхность S вытекает позитивный заряд 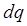 , то за единицу времени
, то за единицу времени 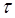 , вытекает заряд, равный силе тока:
, вытекает заряд, равный силе тока:
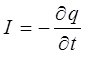
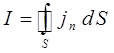
тогда:
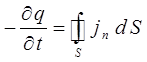
здесь знак «минус» указывает на уменьшение позитивного заряда в объёме V, а символ частной производной подчёркивает, что поверхность S является неподвижной. Учитывая, что:
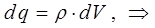
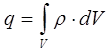
или
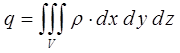
а также, что:
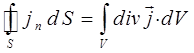
несложно получить такое же уравнение в дифференциальной форме. Так, имеем:
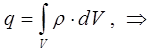
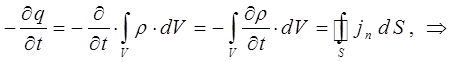
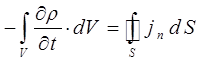
Поскольку по определению, на основании теоремы Остроградского-Гаусса:
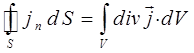
тогда, следовательно, с учётом уравнения:
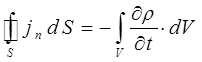
будем иметь соответственно:
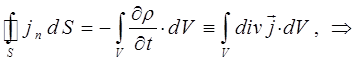
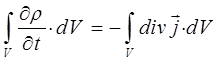
Поскольку интегрирование ведётся по произвольному объёму, то от равенства интегралов можно перейти к равенству соответствующих подынтегральных выражений, тогда, следовательно:
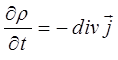
выражения вида:
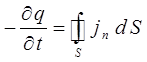
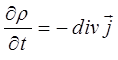
или
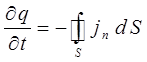
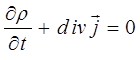
называются также соответственно уравнениями непрерывности в интегральной и дифференциальной формах. Они выражают закон сохранения заряда в электродинамике. Изменение заряда 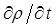 в некотором объёме V, ограниченном поверхностью S, происходит вследствие вытекания этого заряда или вытекания его через эту поверхность. Если распределение зарядов не зависит от времени, определяясь только пространственными координатами
в некотором объёме V, ограниченном поверхностью S, происходит вследствие вытекания этого заряда или вытекания его через эту поверхность. Если распределение зарядов не зависит от времени, определяясь только пространственными координатами 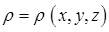 , то в нём – в проводнике, будет протекать стационарный (постоянный) электрический ток. Тогда для стационарного тока уравнение непрерывности в общем случае, будет очевидно определяться выражение вида:
, то в нём – в проводнике, будет протекать стационарный (постоянный) электрический ток. Тогда для стационарного тока уравнение непрерывности в общем случае, будет очевидно определяться выражение вида:
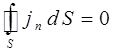
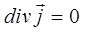
то есть поток вектора 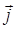 сквозь произвольную замкнутую поверхность S будет равняться нулю. Это в свою очередь означает, что для постоянного тока линии потока будут непрерывными (замкнутыми) кривыми. Иными словами, постоянный ток не имеет источников и стоков зарядов, то есть в середине замкнутой поверхности S в любой из точек
сквозь произвольную замкнутую поверхность S будет равняться нулю. Это в свою очередь означает, что для постоянного тока линии потока будут непрерывными (замкнутыми) кривыми. Иными словами, постоянный ток не имеет источников и стоков зарядов, то есть в середине замкнутой поверхности S в любой из точек 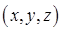 электрические заряды не возникают и не исчезают – на место прошедших в единицу времени через поверхность S зарядов, подходят новые заряды и таким образом поток вектора
электрические заряды не возникают и не исчезают – на место прошедших в единицу времени через поверхность S зарядов, подходят новые заряды и таким образом поток вектора 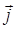 остаётся неизменным. При этом плотность тока остаётся также постоянной. Закон сохранения заряда в электрически нейтральном однородном проводнике определяет постоянство силы тока по всей его длине. Таким образом, плотность и сила тока для стационарных токов, будет определяться выражениями:
остаётся неизменным. При этом плотность тока остаётся также постоянной. Закон сохранения заряда в электрически нейтральном однородном проводнике определяет постоянство силы тока по всей его длине. Таким образом, плотность и сила тока для стационарных токов, будет определяться выражениями:
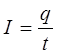
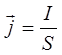
Обратимся теперь к отысканию выражения, которое должно нам дать возможность вычислять в квантовой механике среднюю плотность тока. С этой целью запишем уравнение Шрёдингера для одного измерения:
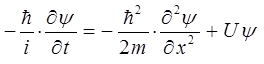
и соответствующее уравнение для 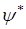 :
:
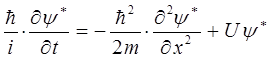
Таким образом, имеем два сопряжённых друг другу уравнения:
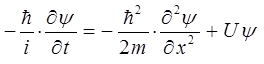
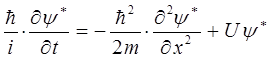
Умножим первое уравнение на 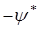 , второе – на
, второе – на 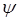 и сложим полученные уравнения между собой. Имеем соответственно:
и сложим полученные уравнения между собой. Имеем соответственно:
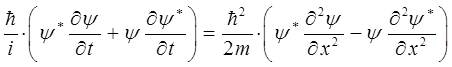
Это можно будет записать также и несколько иным способом:
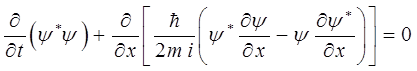
Сравнивая полученное выше соотношение:
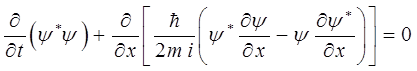
с уравнением непрерывности:
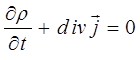
видим, что оба они имеют совершенно одинаковую структуру, только роль плотности 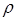 здесь играет произведение
здесь играет произведение 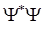 , а роль плотности тока
, а роль плотности тока 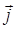 , как это хорошо видно – играет выражение:
, как это хорошо видно – играет выражение:
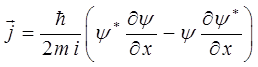
Поскольку 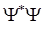 толкуется, как плотность вероятности найти частицу в данном месте пространства, выражение для
толкуется, как плотность вероятности найти частицу в данном месте пространства, выражение для 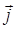 можно истолковать соответственно как плотность «тока вероятности». Смысл последнего выражения в данном контексте оказывается очевидным –
можно истолковать соответственно как плотность «тока вероятности». Смысл последнего выражения в данном контексте оказывается очевидным – 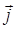 есть вероятность того, что за 1 с частица пройдёт через площадь в 1см2 в направлении положительной нормали к выделенной площадке. Действительно, пусть движение частицы описывается волновой функцией вида:
есть вероятность того, что за 1 с частица пройдёт через площадь в 1см2 в направлении положительной нормали к выделенной площадке. Действительно, пусть движение частицы описывается волновой функцией вида:
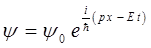
с энергией и импульсом:
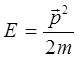
Это значит в свою очередь, что частица имеет импульс определённой величины и определённого направления. В данном случае импульс 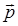 рассматриваемой частицы, совпадает с положительным направлением оси Ox. Координата её, разумеется, остаётся совершенно неопределённой. Написав соответственно комплексно-сопряжённую функцию:
рассматриваемой частицы, совпадает с положительным направлением оси Ox. Координата её, разумеется, остаётся совершенно неопределённой. Написав соответственно комплексно-сопряжённую функцию:
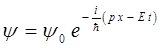
находим:
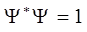
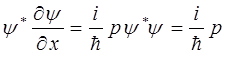
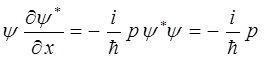
и для тока вероятности получаем:
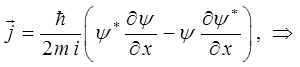
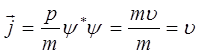
В самом деле, если плотность тока вероятности равна 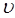 , то средняя плотность тока частиц очевидно должна быть равна
, то средняя плотность тока частиц очевидно должна быть равна 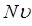 . Представим теперь множество частиц плотностью
. Представим теперь множество частиц плотностью 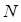 , движущихся в одном направлении со скоростью
, движущихся в одном направлении со скоростью 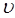 , которые заключены в цилиндре с основанием в 1 см2 и высотой, равной
, которые заключены в цилиндре с основанием в 1 см2 и высотой, равной 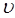 . Число частиц в этом цилиндре, очевидно, будет равно
. Число частиц в этом цилиндре, очевидно, будет равно 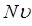 , и все они пройдут за 1 с через основание, то есть создадут ток плотности
, и все они пройдут за 1 с через основание, то есть создадут ток плотности 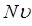 в согласии с результатом, вычисленным на основании формулы:
в согласии с результатом, вычисленным на основании формулы:
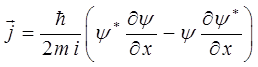
 2015-03-20
2015-03-20 996
996






