-> А-да, В-нет
А- да, В- да
А- нет, В- да
А- нет, В- нет
Установите соответствие между дифференциальными уравнениями и определителями Вронского
-> 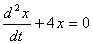 <->
<-> 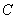
-> 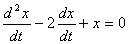 <->
<-> 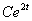
-> 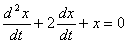 <->
<-> 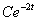
Дифференциальное уравнение 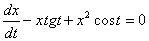 является уравнением
является уравнением
-> Бернулли
однородным первого порядка
с разделяющимися переменными
с полным дифференциалом
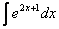 равен
равен
-> 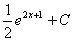
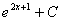
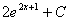

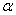 и
и 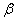 – две б.м.
– две б.м. 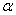 высшего порядка в сравнении с
высшего порядка в сравнении с 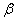 , если
, если
-> 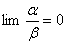
-> 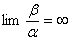
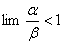
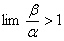
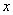 и
и 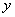 – стороны прямоугольника,
– стороны прямоугольника, 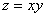 – его площадь. Областью определения функции является множество
– его площадь. Областью определения функции является множество
-> 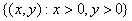
вся плоскость
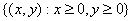
вся плоскость, кроме точки 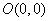
Общий член ряда 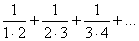 имеет вид
имеет вид
-> 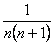
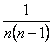
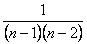
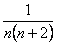
Функция 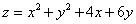 имеет в точке
имеет в точке
-> (–2, –3) – минимум
(–2, –3) – максимум
(2, 3) – стационарную точку
(2, 3) – максимум
Дифференциал функции 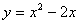 в точке с абсциссой
в точке с абсциссой 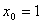 равен (наберите число)
равен (наберите число)
-> 0
Интеграл 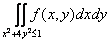 равен повторному интегралу
равен повторному интегралу
-> 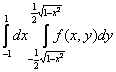
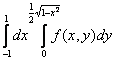
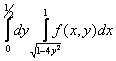
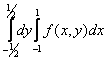
Уравнением Бернулли будет дифференциальное уравнение
-> 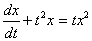
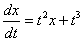
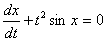
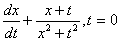
Подберите правильный ответ. -> А-да, В-нет А- да, В- да А- нет, В- да А- нет, В- нет Установите соответствие между дифференциальными уравнениями и определителями Вронского ->
|
|

Сейчас читают про:
 2015-03-22
2015-03-22 682
682







