В ряде транспортных задач необходимо минимизировать время для доставки груза. В таких задачах задаются:
ai – запасы груза пункта отправления;
bj – потребности груза в пунктах назначения;
tij – время доставки груза из i -гов j -й пункт.
Допускается, что коммутационные сети обладают неограниченной пропускной способностью, т.е. tij не зависит от количества перевозимого груза или передаваемой информации.
Время реализации всего плана перевозок определяется максимальным значением времени перевозки в наиболее отдаленные пункты, следовательно, если нашли N допустимых решений, то общее время перевозки 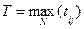 . А для нахождения оптимального решения необходимо найти такое допустимое решение S, время реализации которого минимально.
. А для нахождения оптимального решения необходимо найти такое допустимое решение S, время реализации которого минимально.
Для решения этой задачи используется метод разгрузочных цепей.
Алгоритм решения состоит из следующих шагов
1. Вносятся исходные данные ai, bj, tij в матрицу перевозок.
2. Находится любым методом исходное допустимое решение и заносится в матрицу перевозок. Не пишутся в матрице только нулевые базисные переменные и свободные переменные.
3. Определяется максимальное время реализации, записанного в матрице решения задачи, т.е.  .
.
4. Исследуется клетка с максимальным временем i 1 j 1 на возможность разгрузки, т.е. проверяется в матрице решение на оптимальность. Признаком оптимальности решения транспортной задачи по критерию времени является невозможность построения разгрузочной цепи для клетки с максимальным tij.
5. При наличии разгрузочной цепи исключают переменную 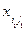 , находящуюся в клетке с максимальным временем, из данного решения и строят новое допустимое решение более, близкое к оптимальному.
, находящуюся в клетке с максимальным временем, из данного решения и строят новое допустимое решение более, близкое к оптимальному.
Разгрузочная цепь является замкнутым циклом, который охватывает как базисные, так и свободные клетки. При этом в разгрузочную цепь не должны входить свободные клетке с tij больше максимального 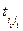 . Разгружаемая цепь изображается всегда так, что разгружаемой клетки приписывается знак «-» и в отрицательных вершинах обязательно находятся базисные переменные.
. Разгружаемая цепь изображается всегда так, что разгружаемой клетки приписывается знак «-» и в отрицательных вершинах обязательно находятся базисные переменные.
Пример. Исходное допустимое базисное решение, найденное, например, диагональным методом, приведено в таблице:
| В1 | В2 | В3 | В4 | ai | |
| А1 | 20 | 5 | 10 | 20 X | |
| А2 | 10 | 15 | 10 | 5 | |
| А3 | 10 | 10 | 5 | 5 | |
| А4 | 5 | 8 | 8 | 10 | |
| bj |
Далее вычеркиваем все свободные клетки с tij ³ t 11, чтобы не использовать их для цикла переноса (это клетка t 14).
Пытаемся разгрузить клетку 1,1. Она имеет сейчас несколько разгрузочных цепей: а) 1,1®2,1®2,2®1,2; б) 1,1®3,1®3,2®1,2;
в) 1,1®3,1®3,3®1,3; г) 1,1®4,1®4,3®1,3.
Однако ни одна из них не позволяет разгрузить клетку за один прием: вначале разгрузим ее на величину 15 по циклу (а), а затем по циклу (б) на величину 5.
В результате получим новое решение в таблице:
| В1 | В2 | В3 | В4 | ai | |
| А1 | 20 Х | 5 | 10 Х | 20 X | |
| А2 | 10 | 15 Х | 10 Х | 5 | |
 А3 А3 | 10 – | 10 Х | 5 + | 5 | |
| А4 | 5 + | 8 | 8 – 5 | 10 | |
| bj |
Для этого решения max(tij)=t 21= t 31= t 44=10. Вычерчиваем все свободные клетки с tij ³10, это 1,3; 2,3; 3,2 и, конечно, 1,1 и 2,2.
Попытаемся разгрузить клетки 2,1; 3,1; 4,4. Клетку 3,1 можно разгрузить по циклу 3,1®4,1®4,3®3,3. Выполним операцию сдвига на х 31=5 и получим решение в следующей таблице:
| В1 | В2 | В3 | В4 | ai | |
| А1 | 20 Х | 5 | 10 Х | 20 X | |
 А2 А2 | 10 _ | 15 Х | 10 Х | 5 + | |
 А3 А3 | 10 Х | 10 Х | 5 | 5 + | |
  А4 А4 | 5 + 5 | 8 | 8 | 10 _ | |
| bj |
Теперь разгрузим клетку 2,1 по циклу 2,1®4,1®4,4®2,4, а затем клетку 4,4 по циклу 4,4®4,3®3,3®3,4. В результате получим решение, данное в таблице:
| В1 | В2 | В3 | В4 | ai | |
| А1 | 20 Х | 5 | 10 Х | 20 X | |
| А2 | 10 Х | 15 Х | 10 Х | 5 | |
| А3 | 10 Х | 10 Х | 5 | 5 | |
  А4 А4 | 5 | 8 Х | 8 | 10 Х | |
| bj |
Для реализации этого решения требуется max(tij)=t 43=8.
Вычеркнем из таблицы свободные клетки с t³8, (т.е. клетку 4,2). Попытаемся разгрузить клетку 4,3. Сделать этого нельзя, т.к. в 4-й строке и в 3-м столбце нет незачеркнутых свободных клеток. Следовательно, решение, записанное в таблице, является оптимальным по критерию времени и найти план, который можно реализовать за время меньше tij =8, невозможно.
 2015-03-22
2015-03-22 1479
1479
