WriteLn('Расстояние будет равно ', S1:7:4, ' км или ', S2:7:4, ' км')

End.

Заметим, что идентификатор должен начинаться с латинской буквы, кроме латинских букв может содержать цифры, знак подчеркивания (_).Разумно, чтобы программа вела диалог с пользователем, т.е. необходимо предусмотреть в ней вывод некоторых пояснительных сообщений. В противном случае даже сам программист может через некоторое время забыть, что необходимо вводить и что является результатом.

Для всех величин в программе объявлен тип Real, что связано со стремлением сделать программу более универсальной и работающей с как можно большими наборами данных.

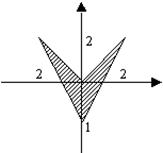Задача 2. Записать логическое выражение, принимающее значение TRUE, если точка лежит внутри заштрихованной области, иначе — FALSE.

Прежде всего обратим внимание на то, что эту сложную фигуру целесообразно разбить на несколько более простых: треугольник, лежащий в I и IV координатных четвертях и треугольник, лежащий во II и III четвертях. Таким образом, точка может попасть внутрь одной из этих фигур, либо на линию, их ограничивающую. Количество отношений, описывающих какую-либо область, обычно совпадает с количеством линий, эту область ограничивающих. Чтобы точка попала внутрь области, необходима истинность каждого из отношений, поэтому над ними выполняется операция AND. Так вся область была разбита на несколько, то между отношениями, описывающими каждую из них, используется операция OR.

Учитывая приведенные здесь соображения и записав уравнения всех ограничивающих фигуру линий, получаем искомое логическое выражение:

(X >= 0) And (Y >= 1.5 * X – 1) And (Y <= X) OR (X <= 0) And (Y >= –1.5 * X – 1) And (Y <= –X)

Задача 3. Вычислить значение выражения:

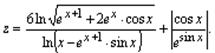
Для решения задачи достаточно ввести все данные, безошибочно записать выражение и вывести результат. Примечание. При решении этой задачи не учитывается область определения выражения, считается, что вводятся только допустимые данные.

Program Expression;

Var X, Z: Real;

Begin

Write('Введите значения переменной X: '); ReadLn(X);

Z:= 6 * ln(sqrt(exp(x+1)+2*exp(x)*cos(x))) /

ln(x - exp(x+3) * sin(x)) + abs(cos(x) / exp(sin(x)));