Метод дихотомии

Метод дихотомии несколько схож с методом бисекции, однако отличается от него критерием отбрасывания концов.

Пусть задана функция 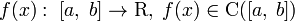. Разобьём мысленно заданный отрезок пополам и возьмём две симметричные относительно центра точк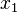и и 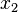так, что:

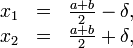
где 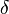— некоторое число в интервале (0; (b–a)/2).

Вычислим значения функции 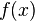в двух новых точках. Сравнением определим, в какой из двух новых точек значение функции 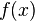максимально. Отбросим тот из концов изначального отрезка, к которому точка с максимальным значением функции оказалась ближе (напомним, мы ищем минимум), то есть:

• Если 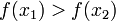, то берётся отрезок 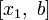, а отрезок 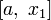отбрасывается.
• Иначе берётся зеркальный относительно середины отрезок 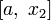, а отбрасывается .

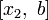Процедура повторяется, пока не будет достигнута заданная точность, к примеру, пока длина отрезка не достигнет удвоенного значения заданной погрешности.