2.2.1 Мета і завдання роботи
Метою роботи є дослідження зв`язку між джерелами (об`єктами) найпростішої форми i гравітаційним ефектом, який вони зумовлюють, та рішення обернених задач методом характерних точок.
Завдання роботи: 1) розрахувати гравітаційне поле від елементарних тіл (куля, скид); 2) вирахувати глибину залягання центра кулі та її масу методом характерних точок.
2.2.2 Короткі теоретичні відомості
Рішенням прямої задачі для правильної геометричної форми є визначення гравiтацiйного ефекту від аномальних об’єктів заданої форми та місця розташування відносно площини, що ототожнюється з площиною денної поверхні.
В гравiрозвiдцi використовується поняття надлишкової густини, тобто аномальні фiзичнi характеристики об`єкту відносно властивостей навколишнього середовища. Тобто, в межах елементарних об’єктів приймають:
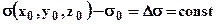 , (2.14)
, (2.14)
де 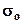 - густина навколишнього середовища;
- густина навколишнього середовища; 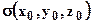 - густина геологічного об`єкту (тіла);
- густина геологічного об`єкту (тіла); 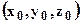 - координати центра тіла.
- координати центра тіла.
Розглянемо рішення прямої задачі для двох елементарних тіл.
Точкова маса (куля). Аномалія 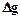 точкової маси для профiля, що проходить над центром кулi (початок координат над центром кулi, вiсь x направлена згiдно профiлю,
точкової маси для профiля, що проходить над центром кулi (початок координат над центром кулi, вiсь x направлена згiдно профiлю, 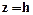 - глибина центра кулi i y = y = 0) визначається з виразу
- глибина центра кулi i y = y = 0) визначається з виразу
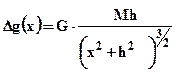 , (2.15)
, (2.15)
де M - надлишкова маса точки, що визначається за формулою:
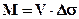 ; (2.16)
; (2.16)
V - об`єм кулі (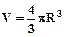 ); R - радіус кулі; h - глибина залягання центра кулі; x - координата по профілю;
); R - радіус кулі; h - глибина залягання центра кулі; x - координата по профілю; 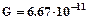
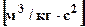 .
.
Друга похідна визначається за формулою:
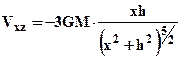 . (2.17)
. (2.17)
Крива 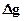 та друга похідна потенціалу сили тяжіння над кулею будуть мати наступний вигляд (ріс.2.4).
та друга похідна потенціалу сили тяжіння над кулею будуть мати наступний вигляд (ріс.2.4).
Обернена задача вирішується з системи рівнянь (за характерними точками при умові, що початок координат співпадає з проекцією центра кулі):
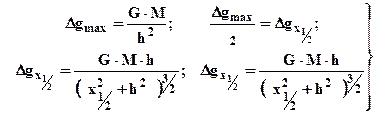 (2.18)
(2.18)
Звідки знаходиться глибина центра кулi h:
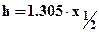 , (2.19)
, (2.19)
де 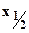 - абсциса половини максимуму
- абсциса половини максимуму 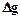 .
.
Надлишкова маса визначається з 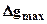
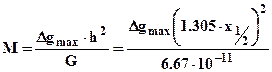 . (2.20)
. (2.20)
В системі СІ
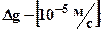
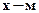
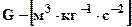 .
.
При вiдомiй надлишковiй густинi об`єкта можна оцiнити його розмiри
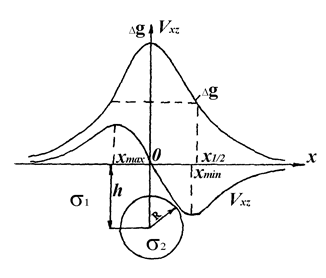
Рисунок 2.4 - Крива 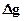 і V
і V 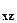 над кулею.
над кулею.
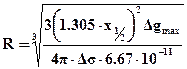 , (2.21)
, (2.21)
та глибину залягання верхньої границi
H = h - R. (2.22)
Вертикальний уступ (скид). Пiд вертикальним уступом розумiють горизонтальний напiвпласт, який обмежений вертикальною границею, нескiнченого простягання по вісi x. Густина порiд уступу рiзна і дорівнює 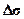 ..Якщо глибину верхньої горизонтальної площини, що обмежує напiвпласт, позначити h1, нижньої - h2, а бокову вертикальну грань сумiстити з вiссю z, то Dg в точках впродовж вісi x (при z = 0; y = 0) буде мати вигляд (рис.2.5).
..Якщо глибину верхньої горизонтальної площини, що обмежує напiвпласт, позначити h1, нижньої - h2, а бокову вертикальну грань сумiстити з вiссю z, то Dg в точках впродовж вісi x (при z = 0; y = 0) буде мати вигляд (рис.2.5).
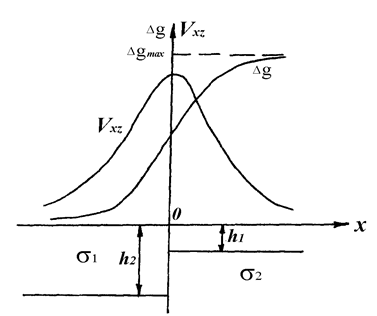
Рисунок 2.5 - Крива 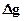 і
і 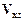 над уступом.
над уступом.
При 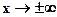 значення
значення 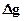 виходить на горизонтальні асимптоти з
виходить на горизонтальні асимптоти з
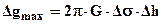 . (2.23)
. (2.23)
Над уступом (скидом)
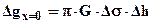
 . (2.24)
. (2.24)
В планi над уступом будуть спостерiгатись паралельнi до простягання уступу iзолiнiї 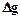 з максимальним ущiльненням iзоаномал над вертикальною гранню. Якщо вiдома надлишкова густина
з максимальним ущiльненням iзоаномал над вертикальною гранню. Якщо вiдома надлишкова густина 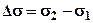 , тодi можна визначити висоту скиду:
, тодi можна визначити висоту скиду:
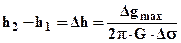 . (2.25)
. (2.25)
2.2.3 Завдання роботи
1. Розрахувати гравiтацiйне поле, яке обумовлене елементарним тiлом (кулею з використання ПЕОМ у середовищі MATHCAD, PASCAL.
Розрахунки провести по профілю 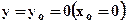 в точках
в точках 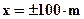 (м), де m = 0, 0.5, 1, 2, 4, 8, 10, 15, 20, 30, 40, 50, 75, 100, а n – остання цифра залікової книжки.
(м), де m = 0, 0.5, 1, 2, 4, 8, 10, 15, 20, 30, 40, 50, 75, 100, а n – остання цифра залікової книжки.
- параметри кулi:
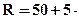 (n - 1) м;
(n - 1) м;
h = 1R, 2R, 3R, 4R.
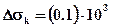 кг/м 3;
кг/м 3;
2. За даними 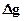 методом характерних точок визначити для кулі h, R, M, якщо
методом характерних точок визначити для кулі h, R, M, якщо 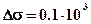 кг/м. Графік Dg використати з розв`язку прямої задачі над кулею.
кг/м. Графік Dg використати з розв`язку прямої задачі над кулею.
3. Визначити амплітуду уступу (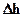 ) і глибину
) і глибину 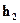 , якщо
, якщо
h = 200 м;
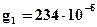 м/c;
м/c;
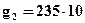 м/c;
м/c;
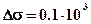 кг/м.
кг/м.
2.2.4 Запитання для самоперевірки
1. Дайте визначення понять пряма та обернена задача гравіметрії.
2. Що означає “надлишкова густина“?
3. За якою формулою визначається 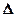 g (0,0,h) над кулею?
g (0,0,h) над кулею?
4. За якою формулою визначається 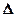 g над уступом для випадку
g над уступом для випадку 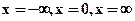 .
.
5. Якій точці кривої 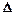 g відповідає границя площини уступу?
g відповідає границя площини уступу?
6. Як змінюється характер кривої  g над кулею для випадку
g над кулею для випадку
h =const, R - змінна;
R =const, h - змінна?
7. В чому суть рішення зворотної задачі над кулею?
2.2.5 Форма звітності
1. Представити результати розрахунків для заданих розмірів елементарних тіл і побудовані графіки розподілу гравітаційного поля над ними.
2. Проаналізувати графіки Dg над кулею різних радіусів і на різних глибинах.
3. Навести розрахунки і параметри кулі за рішенням оберненої задачі.
4. Привести дані рішення оберненої задачі над скидом.
Література
Основы геофизических методов разведки \ Толстой М.И. и др. – К.: Вища школа. Главное издательство, 1985. – 327 с.
 2015-03-27
2015-03-27 756
756








