Пусть 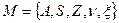 - конечный автомат. Тогда по любой входной строке
- конечный автомат. Тогда по любой входной строке 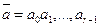 длины r и по любому начальному состоянию
длины r и по любому начальному состоянию 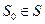 однозначно определяется строка длины r внутренних состояний
однозначно определяется строка длины r внутренних состояний 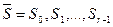 , которая получается последовательным применением отображения
, которая получается последовательным применением отображения 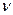 . Точнее:
. Точнее: 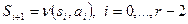 . Аналогично строка на выходе определяется последовательным применением отображения
. Аналогично строка на выходе определяется последовательным применением отображения 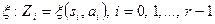 . Поэтому рассмотрим автомат как устройство, перерабатывающее пары, состоящие из состояния
. Поэтому рассмотрим автомат как устройство, перерабатывающее пары, состоящие из состояния 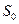 и
и 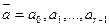 в строки
в строки 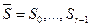 и
и 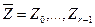 . С помощью функций
. С помощью функций 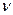 и
и 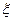 можно определить функции
можно определить функции 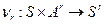 ,
, 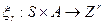 , которые строятся по функциям
, которые строятся по функциям 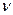 и
и 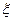 , заданным в описании автомата М.
, заданным в описании автомата М.
Пример. Автомат задан диаграммой:
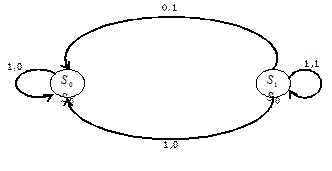
Пусть входная строка 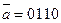 и начальное состояние
и начальное состояние 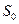 , тогда
, тогда 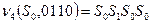 ,
, 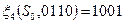 .
.
Увеличение числа внутренних состояний автомата в реальном устройстве приводит к росту количества электронных схем, к уменьшению надежности, к усложнению отладки и т. д. Поэтому число необходимых состояний автомата, предназначенного для выполнения определенных действий, стремятся уменьшить, не ограничивая его возможностей.
Этим объясняется важность следующей задачи. Предположим, что входной и выходной алфавиты фиксированы. Возникает следующий вопрос. Можно ли заменить автомат 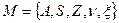 автоматом с меньшим числом внутренних состояний
автоматом с меньшим числом внутренних состояний 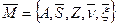 , но с той же функцией, переводящей входы в выходы?
, но с той же функцией, переводящей входы в выходы?
Определение 1: Говорят, что автомат 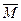 покрывает автомат
покрывает автомат 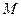 , если входной и выходной алфавиты у них общие и существует функция
, если входной и выходной алфавиты у них общие и существует функция 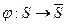 , такая что для любого положительного числа
, такая что для любого положительного числа 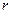 имеет место условие:
имеет место условие:
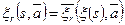
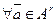 .
.
Определение 2: Автомат, который нельзя покрыть меньшим автоматом, называется минимальным. Будем писать: 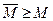 , если
, если 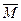 покрывает
покрывает 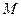 .
.
Теорема 1: Отношение покрытий рефлексивно и транзитивно.
Доказательство очевидно.
Определение 3: Автоматы 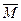 и
и 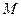 называются эквивалентными, если автомат
называются эквивалентными, если автомат 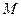 покрывает
покрывает 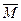 и автомат
и автомат 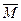 покрывает
покрывает 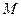 . В этом случае пишут:
. В этом случае пишут: 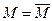 .
.
Это означает, что кроме функции 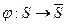 со свойством, указанным в предыдущем определении, существует еще функция
со свойством, указанным в предыдущем определении, существует еще функция 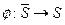 со следующим свойством:
со следующим свойством: 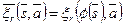 при
при 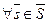 и
и 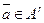 .
.
Следствие: Отношение эквивалентности автоматов рефлексивно, транзитивно и симметрично.
Пусть 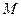 и
и 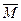 – автоматы с общими входными и выходными алфавитами.
– автоматы с общими входными и выходными алфавитами.
Определение 4:Морфизмом называется такое отображение 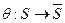 , что
, что 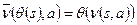 и
и 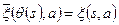
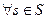 и
и 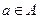 . Если
. Если 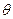 сюрьективно, то морфизм называется эпиморфизмом. Если
сюрьективно, то морфизм называется эпиморфизмом. Если 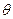 - биекция, то морфизм называется изоморфизмом.
- биекция, то морфизм называется изоморфизмом.
Теорема 2: Пусть 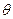 эпиморфизм автомата
эпиморфизм автомата 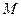 на
на 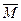 . Тогда для любой входной строки
. Тогда для любой входной строки 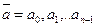 и любого начального состояния
и любого начального состояния 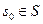 входная строка
входная строка 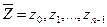 автомата
автомата 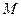 совпадает с входной строкой автомата
совпадает с входной строкой автомата 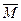 , если начальное состояние
, если начальное состояние 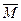 равно
равно 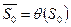 .
.
Доказательство: Доказательство можно провести индукцией по числу 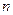 с индуктивным шагом:
с индуктивным шагом:
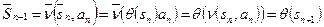 ;
;
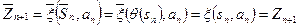 .
.
Следствие: Любой эпиморфизм 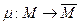 определяет покрытие автомата
определяет покрытие автомата 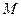 автоматом
автоматом 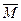 . Изоморфизм автоматов
. Изоморфизм автоматов 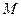 и
и 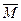 с общим входным и выходным алфавитами есть биекция
с общим входным и выходным алфавитами есть биекция 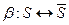 , такая, что для всякого начального состояния
, такая, что для всякого начального состояния 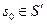 и всякой входной строки
и всякой входной строки 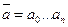 автоматы
автоматы 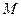 и
и  выдают одну и ту же выходную строку, проходя через соответствующие промежуточные состояния.
выдают одну и ту же выходную строку, проходя через соответствующие промежуточные состояния.
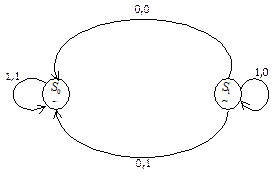
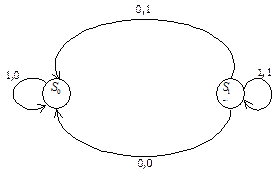
Пример. Автоматы, представленные следующими ориентированными графами, изоморфны.
 2015-03-27
2015-03-27 788
788








