2015-03-07
3710
Пример. Для откорма животных на ферме в их ежедневный рацион необходимо включить не менее 33-х единиц питательного вещества A, 23-х единиц вещества B и 12-ти единиц вещества C. Для откорма используется 3 вида кормов. Данные о содержании питательных веществ и стоимости весовой единицы каждого корма даны в таблице.
| A (усл. ед.) | B (усл. ед.) | C (усл. ед.) | Стоимость (руб.) | |
| Весовая единица корма I | ||||
| Весовая единица корма II | ||||
| Весовая единица корма III |
Требуется составить наиболее дешёвый рацион, при котором каждое животное получило бы необходимое количество питательных веществ A, B и C.
Математическая постановка задачи. Пусть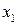 
, 
, 
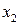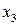— количества кормов I, II, III видов, включаемые в ежедневный рацион (
, 
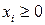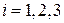). Тогда должно быть:
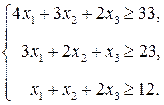
При этом целевая функция (стоимость рациона)
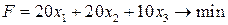
1. Зададим начальное приближение:
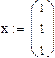
2. Запишем все коэффициенты в матричном виде:
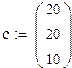
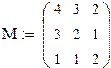
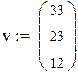
3. Введем целевую функцию в виде:
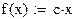
4. Запишем функцию Given.
5. Запишем ограничения в виде:
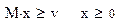
6. Запишем функцию минимизации
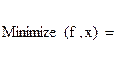
после чего получим оптимальный план
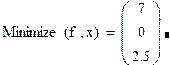
7. Найдем значение целевой функции в точке минимума:
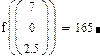
ВАРИАНТЫ ЗАДАНИЙ
Максимизировать целевую функцию Z, приведенную в таблице
| Вариант | ЦФ | Ограничения |
| Z=9 х 1+10 х 2+16 х 3 | 18 х 1+15 х 2+12 х 3 ≤ 360 6 х 1+4 х 2+8 х 3 ≤ 192 –10 х 1+3 х 2+3 х 3 ≤ 30 х 1 ≥ 0, х 2 ≥ 0, х 3 ≥ 0 | |
| Z=7 х 1+12 х 2+14 х 3 | 28 х 1+25 х 2+22 х 3 ≤ 560 4 х 1–40 х 2+6 х 3 ≤ 100 –10 х 1+30 х 2+5 х 3 ≤ 50 х 1 ≥ 0, х 2 ≥ 0, х 3 ≥ 0 | |
| Z=2 х 1+3 х 2+4 х 3 | –5 х 1+6 х 2+7 х 3 ≤ 20 8 х 1–9 х 2+10 х 3 ≤ 30 11 х 1+12 х 2–13 х 3 ≤ 40 х 1 ≥ 0, х 2 ≥ 0, х 3 ≥ 0 | |
| Z=3 х 1+4 х 2+2 х 3 | 15 х 1–16 х 2+17 х 3 ≤ 120 –18 х 1+19 х 2+20 х 3 ≤ 130 21 х 1+22 х 2–23 х 3 ≤ 140 х 1 ≥ 0, х 2 ≥ 0, х 3 ≥ 0 | |
| Z=3 х 1+4 х 2+2 х 3 | 15 х 1+16 х 2–17 х 3 ≤ 120 18 х 1–19 х 2+20 х 3 ≤ 130 –21 х 1+22 х 2+23 х 3 ≤ 140 х 1 ≥ 0, х 2 ≥ 0, х 3 ≥ 0 | |
| Z=7 х 1+12 х 2+14 х 3 | 48 х 1+25 х 2+22 х 3 ≤ 500 4 х 1–20 х 2+6 х 3 ≤ 20 –10 х 1+10 х 2+5 х 3 ≤ 50 х 1 ≥ 0, х 2 ≥ 0, х 3 ≥ 0 | |
| Z=8 х 1+11 х 2+15 х 3 | 50 х 1+26 х 2–20 х 3 ≤ 30 4 х 1–20 х 2+6 х 3 ≤ 20 –10 х 1+10 х 2+5 х 3 ≤ 50 х 1 ≥ 0, х 2 ≥ 0, х 3 ≥ 0 | |
| Z=10 х 1+20 х 2+30 х 3 | –30 х 1+40 х 2+50 х 3 ≤ 70 10 х 1–20 х 2+20 х 3 ≤ 30 20 х 1+30 х 2–40 х 3 ≤ 50 х 1 ≥ 0, х 2 ≥ 0, х 3 ≥ 0 | |
| Z=15 х 1+25 х 2+35 х 3 | 30 х 1+40 х 2–50 х 3 ≤ 70 10 х 1–20 х 2+20 х 3 ≤ 30 –20 х 1+30 х 2+40 х 3 ≤ 50 х 1 ≥ 0, х 2 ≥ 0, х 3 ≥ 0 | |
| Z=10 х 1+5 х 2+45 х 3 | 30 х 1+40 х 2–50 х 3 ≤ 70 10 х 1–20 х 2+20 х 3 ≤ 30 –20 х 1+30 х 2+40 х 3 ≤ 50 х 1 ≥ 0, х 2 ≥ 0, х 3 ≥ 0 | |
| Z=5 х 1+5 х 2+5 х 3 | 20 х 1+20 х 2–20 х 3 ≤ 120 30 х 1–30 х 2+30 х 3 ≤ 80 –40 х 1+40 х 2+40 х 3 ≤ 90 х 1 ≥ 0, х 2 ≥ 0, х 3 ≥ 0 | |
| Z=12 х 1+12 х 2+12 х 3 | 12 х 1+13 х 2–14 х 3 ≤ 12 24 х 1–25 х 2+24 х 3 ≤ 24 –48 х 1+48 х 2+49 х 3 ≤ 48 х 1 ≥ 0, х 2 ≥ 0, х 3 ≥ 0 |
ЛАБОРАТОРНАЯ РАБОТА № 18
ЗАДАЧА ПОСТРОЕНИЯ ОСТОВНОГО ДЕРЕВА
