2015-03-07
472
Определение. Задачи математического программирования с требованием целочисленности переменных называются задачами целочисленного программирования.
Задача о назначениях - задача целочисленного программирования. Она решается проще, чем задача линейного программирования, но это, скорее, исключение, чем правило. Обычно требование целочисленности усложняет задачу.
Запишем задачу линейного программирования в стандартной форме с требованием целочисленности.
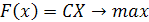
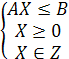
На практике применяется несколько способов решения таких задач.
1. Решить эту задачу симплекс-методом, и если получится нецелочисленное оптимальное решение, то округлить до ближайшего допустимого целочисленного решения. Этот путь возможен тогда, когда значения X в оптимальном решении достаточно велики.
2. Найти точное решение целочисленной задачи линейного программирования (ЦЗЛП).
Важными методами нахождения таких решений являются методы отсечений нецелочисленных решений. Отсечения должны удовлетворять следующим условиям.
|
|
|
1. Они должны отсекать оптимальное нецелочисленное решение задачи, полученное на предыдущем шаге.
2. Они не должны отсечь ни одного допустимого целочисленного решения.
Разберем один из таких методов - метод отсечения Гомори.
Алгоритм решения ЦЗЛП методом Гомори
1. Решаем задачу линейного программирования без требования целочисленности симплекс-методом.
| X1 | Х2 | … | Хk | Хk+1 | … | Xn | ||
| X1 | … |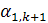 
| 
| 
| ||||
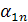
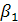
| X2 | … |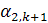 
| 
| 
| ||||
| … | … | … | … | … | … | … | … | … |
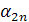
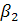
| Хk | … |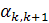 
| 
| 
|
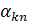
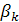
Х1*=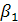
Х2*=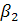
…………
Хk*=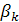
Хk+1*=0
…………
Хn*=0
Если все значения в оптимальном решении целочисленные, то получено решение ЦЗЛП. Если множество допустимых решений исходной задачи пусто или целевая функция на этом множестве не ограничена, то же самое будет верно и для ЦЗЛП.
2.Определение. Целой частью числа X называется ближайшее целое число, меньшее X. Обозначается [X].
Например, если х = 3,45; [x] = 3.
Определение. Дробной частью числа X называется разность
между X и целой частью этого числа.
Например, если x = 3,45; {x} =0,45.
На втором шаге всегда есть хотя бы одно нецелое среди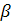 
. Выбираем из нецелых 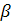то, которое имеет наибольшую дробную часть, обозначим такое 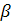через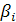 
.
Гомори доказал, что неравенство
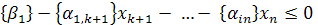определяет отсечение, удовлетворяющее всем сформулированным выше требованиям. Это неравенство добавляем к ограничениям задачи и возвращаемся на шаг 1, и так до тех пор, пока не получится оптимальное целочисленное решение. Если на каком-то шаге алгоритма все коэффициенты 
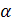- целочисленные, а среди 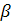есть нецелые, то задача не имеет целочисленного решения.
|
|
|
Пример. Фермеры некоторого района решили оборудовать сортировочный ток. На закупку оборудования имеется 34 тыс.$, имеется площадь для тока размером 60 м2, имеется два типа сортировочных машин, которые можно закупить. Машина типа А стоит 3 тыс.$, занимает площадь 3 м2 с учетом проходов и сортирует 2 тонны зерна за смену; машина типа В стоит 4 тыс.$, занимает площадь 5 м2 с учетом проходов и сортирует 3 тонны зерна за смену. Поставщик сообщил, что машин тина В в наличии не более 8. Сколько и каких машин нужно закупить, чтобы обеспечить максимальную производительность тока за смену, не превысив имеющихся ресурсов?
Введём управляющие переменные. Обозначим x1 - количество купленных машин типа А, х2 - количество купленных машин типа В.
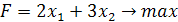
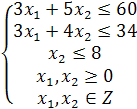
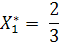
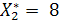
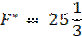
| X1 | X2 | Х3 | Х4 | х5 | ||
| Х3 | ||||||
| х4 | ||||||
| Х5 | ||||||
| F | -2 | -3 | ||||
| X3 | -5 | |||||
| X4 | -4 | |||||
| Х2 | ||||||
| F | -2 | |||||
| Х3 | -1 | -1 | ||||
| X1 | 1/3 | -4/3 | 2/3 | |||
| Х2 | ||||||
| F | 2/3 | 1/3 | 251/3 |
По условию задачи очевидно, что закупать 2/3 машины типа А бессмысленно. Если данное решение округлить до допустимого решения, то получим
х1 =0
х2 = 8.
F = 24
Найдём точное решение. Строим отсечение.
;
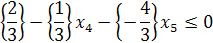
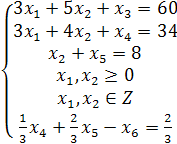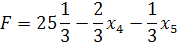
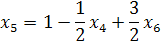
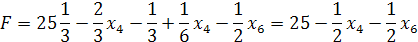
| X1 | Х2 | Х3 | X4 | X5 | X6 | ||
| -1 | -1 | ||||||
| 1/3 | -4/3 | 2/3 | |||||
| 1/3 | 2/3 | -1 | 2/3 | ||||
| Х3 | -1/2 | -3/2 | |||||
| X1 | -2 | ||||||
| х2 | -1/2 | 3/2 | |||||
| Х5 | 1/2 | -3/2 | |||||
| F | 1/2 | 1/2 |
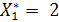
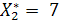
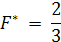
Полученное решение целочисленно. Нужно закупить две машины типа А и семь машин типа В.
Вопросы для самоконтроля
1. Какая задача линейного программирования называется целочисленной?
2. Структура экономико-математической модели задачи
целочисленного программирования?
3. Какие существуют методы решения задач целочисленного программирования?
4. Пояснить суть метода Гомори.
5. Что называется сечением Гомори?
6. Пояснить принципиальную суть метода ветвей и границ.
7. Пояснить происхождение названия метода ветвей и границ.
