AB = a, BC = b - қабырғалар;
S - аудан;
AC = m; BD = n - диагональдар;
ha, hb - биіктіктер;
Ð A, Ð B, Ð C, Ð D - бұрыштар.
Формуланың аты Формула
Периметр P = 2(a + b)
Бұрыштардың қосындысы
Ð A = Ð C; Ð B = Ð D; Ð A + Ð B = Ð B + Ð C = 180°
Диагональдардың m 2 + n 2 = 2(a 2 + b 2)
квадраттарының қосындысы
Аудан S = a×ha = b×hb; S = a×b × sin b
Ромб
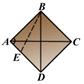 AB = BC = CD = DA = a - қабырғалар;
AB = BC = CD = DA = a - қабырғалар;
m, n - диагональдар;
ВЕ - биіктік;
AC ^ BD
Формуланың аты Формула
Периметр Р = 4 а
Аудан S = a×h; S = m×n /2; S = a 2× sin A
Квадрат 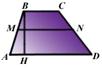
AB = BC = CD = DA - қабырғалар, BC || AD,
BC = a, AD = b - табандар
BH = h - биіктік, MN = m - орта сызық
Формуланың аты Формула
Орта сызық m= (a+b)/2
Аудан S = (a+b)h/2; S = mh
Төртбұрыш 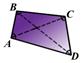
Қабырғалар - AB = a, BC = b, CD = c, DA = a Диагональдар - AC = m, BD = n Бұрыштар - Ð A, Ð B, Ð C, Ð D
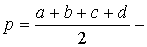 жарты периметр
жарты периметр
r - іштей сызылған шеңбердің радиусы.
Формуланың аты Формула
Бұрыштардың қосындысы Ð A + Ð B + Ð C + Ð D = 360°
Іштей сызылған төртбұрыштың Ð A + Ð B + Ð C + Ð D = 180°
қарама-қарсы жатқан бұрыштардың қасиеті
Диагональдардың көбейтіндісі m×n = a×c + b×d
(Птолемей теоремасы)
Сырттай сызылған төртбұрыштың a + c = b + d
қарама-қарсы жатқан бұрыштардың қасиеті
Сырттай сызылған төртбұрыштың ауданы S = pr
Тік бұрышты үшбұрыш 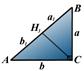
- Ð C = 90°, AB = c - гипотенуза;
- AC = b, BC = a - катеттер;
- a 1, b 1 - каттердің гипотенузаға проекциялары;
- r - іштей сызылған шеңбердің радиусы;
- R - сырттай сызылған шеңбердің радиусы;
- CH 3 - биіктік.
| Формуланың аты | Формула |
| · Сүйір бұрыштарының қосындысы | Ð A + Ð B = 90° |
| · Пифагор теоремасы | a 2 + b 2 = c 2 |
| · Метрикалық қатыстар | CH 32 = a 1 b 1, a 2 = ca 1, b 2 = cb 1 |
| · Бұрыштар мен қабырғалардың арасындағы байланыс | a = c sin A, b = c cos B, a = b tg A, |
| · Аудан | S = ab /2 |
| · Іштей сызылған шеңбердің радиусы | r = (a + b + c) /2 |
| · Сырттай сызылған шеңбердің радиусы | R = c /2 |
Үшбұрыштар теңдігінің белгілері. 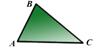
Сөйлемдердің шарттары.
1. AB = A 1 B 1, AC = A 1 C 1, Ð A = Ð A 1 немесе,
CB = C 1 B 1, CA = C 1 A 1, Ð C = Ð C 1 немесе,
BA = B 1 A 1, BC = B 1 C 1, Ð B = Ð B 1
2. AC = A 1 C 1, Ð A = Ð A 1, Ð C = Ð C 1 немесе,
AB = A 1 B 1, Ð A = Ð A 1, Ð B = Ð B 1 немесе,
BC = B 1 C 1, Ð B = Ð B 1, Ð C = Ð C 1
3. AB = A 1 B 1, AC = A 1 C 1, 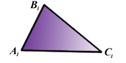 BC = B 1 C 1
BC = B 1 C 1
Қорытындысы
1. 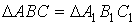 2. 2.
2. 2. 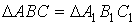 3. 3.
3. 3. 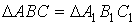
Үшбұрыш
-
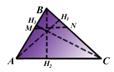 AB = c, AC = b, BC = a - үшбұрыштың қабырғалары;
AB = c, AC = b, BC = a - үшбұрыштың қабырғалары; - AH 1, BH 2, CH 3 - үшбұрыштың биіктіктері;
- Ð A = a, Ð B = b, Ð C = g - үшбұрыштың ішкі бұрыштары;
- a', b', g' - үшбұрыштың сыртқы бұрыштары;
- MN - үшбұрыштың орта сызығы;
- p - жарты периметр;
- Р -ұшбұрыштың периметрі;
- AD 1, BD 2, CD 3 - үшбұрыштың медианалары;
- AA 1, BB 1, CC 1 - үшбұрыштың биссектриссалары;
- r - ұшбұрышқа іштей сызылған шеңбердің радиусы;
- R - үшбұрышты сырттай сызылған шеңбердің радиусы.
| Формуланың аты | Формула |
| · Периметр | P = a + b + c, p = (a + b + c) /2 |
| · Ішкі бұрыштарының қосындысы | Ð A + Ð B + Ð C = 180° |
| · Сыртқы бұрыштарының қасиеттері | a' = b + g, b' = a + g, g' = b + a; a' > b, a' > g, b' > a, b' > g, g' > a, g' > b |
| · Үшбұрыш теңсіздігі | a < b + c, b < a + c, c < a + b |
Биіктер 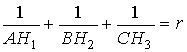 | |
| · Медианалар | 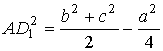 |
| · Биссектрисалардың қасиеті мұнда бұрыштың биссектрисасы а қабырғаны бөлетін кесінділер | 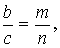 мұнда m, n - A бұрыштың биссектрисасы a қабырғаны бөлетін кесінділер мұнда m, n - A бұрыштың биссектрисасы a қабырғаны бөлетін кесінділер |
| · Орта сызықтың қасиеті | 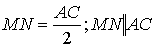 |
| · Синустар теоремасы | 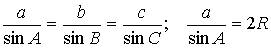 |
| · Косинустар теоремасы | 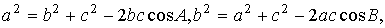 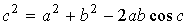 |
· Сырттай сызылған шеңбердің радиусы 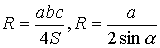 | |
| · Аудан | 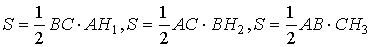 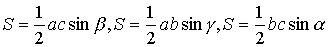 |
| · Герон формуласы | 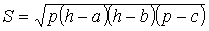 |
Шеңбер мен дөңгелек
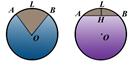
l - ALB доғаның ұзындығы,
LH - биіктік,
D - диаметр, 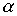 - ALB - доғаның градуатық өлшемі,
- ALB - доғаның градуатық өлшемі,
R = OA = OB - радиус,
C - шеңбердің ұзындығы.
Формуланың аты Формула
Шеңбердің доғасының ұзындығы 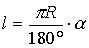 Шеңбердің ұзындығы
Шеңбердің ұзындығы 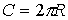 Дөңгелектің ауданы
Дөңгелектің ауданы 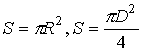
Сектордың ауданы 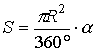
Сегменттің ауданы 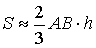
 2015-03-07
2015-03-07 1065
1065








