Приложение 1
Контрольная работа №1
по теме «Логика высказываний. Булевы функции. Логика предикатов».
I вариант
1. Даны множества: 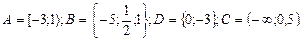
Найти: 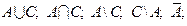
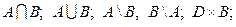 A
A  Z; B ∩ N; D
Z; B ∩ N; D  Z.
Z.
Указать все подмножества множества B.
2. Определить значение истинности высказывания 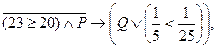
где: P: «Для любого вещественного х выполняется неравенство 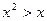 »;
»;
Q: «Существует трапеция с двумя прямыми углами».
- Упростить формулу:
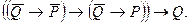
- Представить булеву функцию в виде СДНФ с помощью равносильных преобразований:
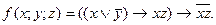
- Дана функция:
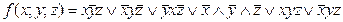
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P(x): «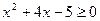 », Q(x): «
», Q(x): «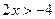 », если:
», если:
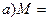 R; б)
R; б) 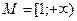 .
.
- Найти множество истинности предиката, если
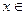 R:
R:
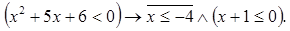 |
II вариант
1. Даны множества: 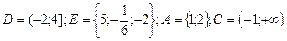
Найти: 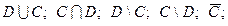
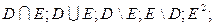 D ∩ N, E \ Z; A ∩ N. Указать все подмножества множества E.
D ∩ N, E \ Z; A ∩ N. Указать все подмножества множества E.
2. Определить значение истинности высказывания 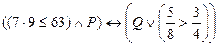 ,
,
где: P: «Существует наибольшее целое отрицательное число»;
Q: «Для любого вещественного х выполняется: 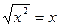 ».
».
3. Упростить формулу: 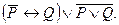
- Представить булеву функцию в виде СДНФ с помощью равносильных преобразований:
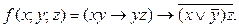
5. Дана функция: 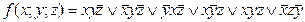
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P(x): «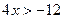 », Q(x): «
», Q(x): «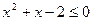 », если:
», если:
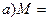 R; б)
R; б) 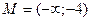 .
.
- Найти множество истинности предиката, если
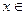 R:
R:
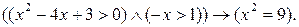
III вариант
1. Даны множества: 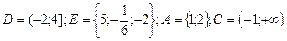
Найти: 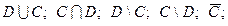
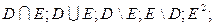 D ∩ N, E \ Z; A ∩ N. Указать все подмножества множества E.
D ∩ N, E \ Z; A ∩ N. Указать все подмножества множества E.
2. Определить значение истинности высказывания 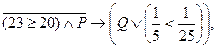
где: P: «Для любого вещественного х выполняется неравенство 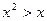 »;
»;
Q: «Существует трапеция с двумя прямыми углами».
3. Упростить формулу: 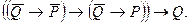
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 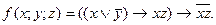
5. Дана функция: 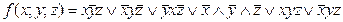
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P(x): «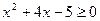 », Q(x): «
», Q(x): «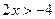 », если:
», если:
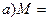 R; б)
R; б) 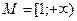 .
.
7. Найти множество истинности предиката, если 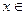 R:
R:
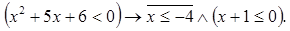 |
IV вариант
1. Даны множества: 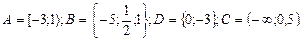
Найти: 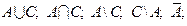
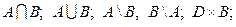 A
A 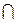 Z; B ∩ N; D
Z; B ∩ N; D  Z.
Z.
Указать все подмножества множества B.
2. Определить значение истинности высказывания 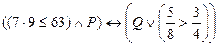 ,
,
где: P: «Существует наибольшее целое отрицательное число»;
Q: «Для любого вещественного х выполняется: 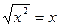 ».
».
3. Упростить формулу: 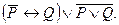
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 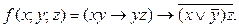
5. Дана функция: 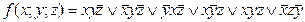
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P(x): «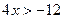 », Q(x): «
», Q(x): «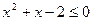 », если:
», если:
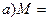 R; б)
R; б) 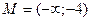 .
.
7. Найти множество истинности предиката, если 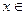 R:
R:
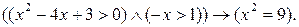
V вариант
1. Даны множества: 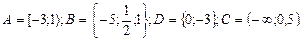
Найти: 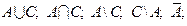
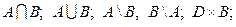 A
A 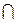 Z; B ∩ N; D
Z; B ∩ N; D  Z.
Z.
Указать все подмножества множества B.
2. Определить значение истинности высказывания 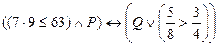 ,
,
где: P: «Существует наибольшее целое отрицательное число»;
Q: «Для любого вещественного х выполняется: 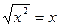 ».
».
3. Упростить формулу: 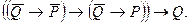
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 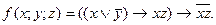
5. Дана функция: 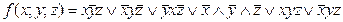
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P(x): «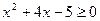 », Q(x): «
», Q(x): «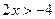 », если:
», если:
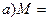 R; б)
R; б) 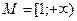 .
.
7. Найти множество истинности предиката, если 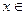 R:
R:
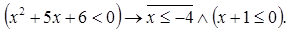 |
VI вариант
1. Даны множества: 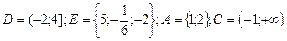
Найти: 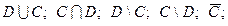
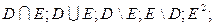 D ∩ N, E \ Z; A ∩ N. Указать все подмножества множества E.
D ∩ N, E \ Z; A ∩ N. Указать все подмножества множества E.
2. Определить значение истинности высказывания 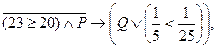
где: P: «Для любого вещественного х выполняется неравенство 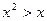 »;
»;
Q: «Существует трапеция с двумя прямыми углами».
3. Упростить формулу: 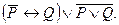
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 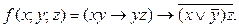
5. Дана функция: 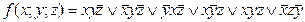
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P(x): «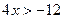 », Q(x): «
», Q(x): «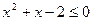 », если:
», если:
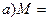 R; б)
R; б) 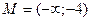 .
.
7. Найти множество истинности предиката, если 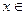 R:
R:
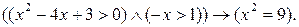
VII вариант
1. Даны множества: 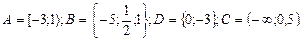
Найти: 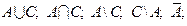
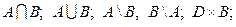 A
A 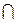 Z; B ∩ N; D
Z; B ∩ N; D 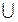 Z.
Z.
Указать все подмножества множества B.
2. Определить значение истинности высказывания 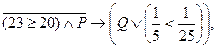
где: P: «Для любого вещественного х выполняется неравенство 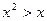 »;
»;
Q: «Существует трапеция с двумя прямыми углами».
3. Упростить формулу: 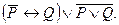
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 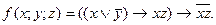
5. Дана функция: 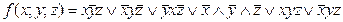
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P(x): «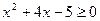 », Q(x): «
», Q(x): «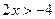 », если:
», если:
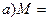 R; б)
R; б) 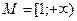 .
.
7. Найти множество истинности предиката, если 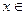 R:
R:
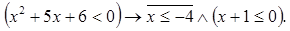 |
VIII вариант
1. Даны множества: 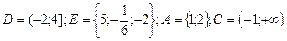
Найти: 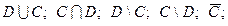
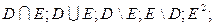 D ∩ N, E \ Z; A ∩ N. Указать все подмножества множества E.
D ∩ N, E \ Z; A ∩ N. Указать все подмножества множества E.
2. Определить значение истинности высказывания 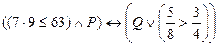 ,
,
где: P: «Существует наибольшее целое отрицательное число»;
Q: «Для любого вещественного х выполняется: 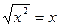 ».
».
3. Упростить формулу: 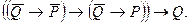
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 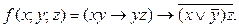
5. Дана функция: 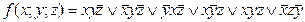
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P(x): «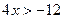 », Q(x): «
», Q(x): «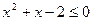 », если:
», если:
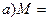 R; б)
R; б) 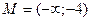 .
.
7. Найти множество истинности предиката, если 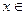 R:
R:
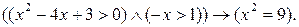
IX вариант
1. Даны множества: 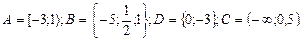
Найти: 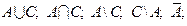
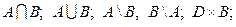 A
A 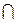 Z; B ∩ N; D
Z; B ∩ N; D  Z.
Z.
Указать все подмножества множества B.
2. Определить значение истинности высказывания 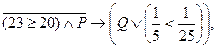
где: P: «Для любого вещественного х выполняется неравенство 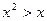 »;
»;
Q: «Существует трапеция с двумя прямыми углами».
3. Упростить формулу: 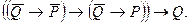
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 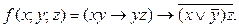
5. Дана функция: 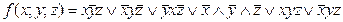
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P(x): «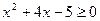 », Q(x): «
», Q(x): «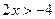 », если:
», если:
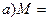 R; б)
R; б) 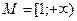 .
.
7. Найти множество истинности предиката, если 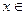 R:
R:
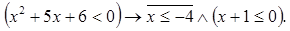 |
X вариант
1. Даны множества: 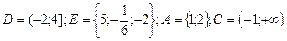
Найти: 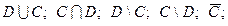
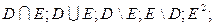 D ∩ N, E \ Z; A ∩ N. Указать все подмножества множества E.
D ∩ N, E \ Z; A ∩ N. Указать все подмножества множества E.
2. Определить значение истинности высказывания 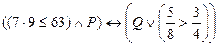 ,
,
где: P: «Существует наибольшее целое отрицательное число»;
Q: «Для любого вещественного х выполняется: 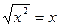 ».
».
3. Упростить формулу: 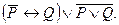
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 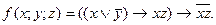
5. Дана функция: 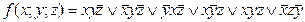
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P(x): «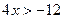 », Q(x): «
», Q(x): «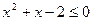 », если:
», если:
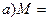 R; б)
R; б) 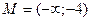 .
.
7. Найти множество истинности предиката, если 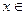 R:
R:
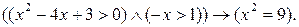
XI вариант
1. Даны множества: 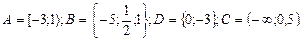
Найти: 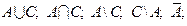
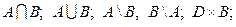 A
A 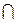 Z; B ∩ N; D
Z; B ∩ N; D 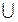 Z.
Z.
Указать все подмножества множества B.
2. Определить значение истинности высказывания 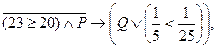
где: P: «Для любого вещественного х выполняется неравенство 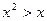 »;
»;
Q: «Существует трапеция с двумя прямыми углами».
3. Упростить формулу: 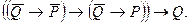
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 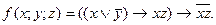
5. Дана функция: 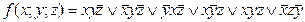
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P(x): «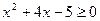 », Q(x): «
», Q(x): «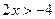 », если:
», если:
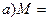 R; б)
R; б) 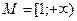 .
.
7. Найти множество истинности предиката, если 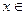 R:
R:
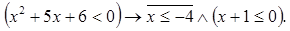 |
XII вариант
1. Даны множества: 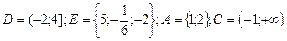
Найти: 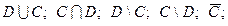
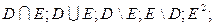 D ∩ N, E \ Z; A ∩ N. Указать все подмножества множества E.
D ∩ N, E \ Z; A ∩ N. Указать все подмножества множества E.
2. Определить значение истинности высказывания 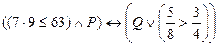 ,
,
где: P: «Существует наибольшее целое отрицательное число»;
Q: «Для любого вещественного х выполняется: 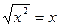 ».
».
3. Упростить формулу: 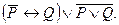
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 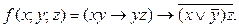
5. Дана функция: 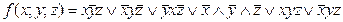
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P(x): «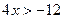 », Q(x): «
», Q(x): «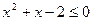 », если:
», если:
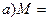 R; б)
R; б) 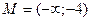 .
.
7. Найти множество истинности предиката, если 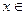 R:
R:
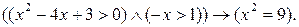
XIII вариант
1. Даны множества: 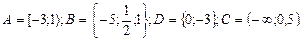
Найти: 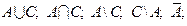
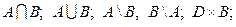 A
A 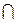 Z; B ∩ N; D
Z; B ∩ N; D  Z.
Z.
Указать все подмножества множества B.
2. Определить значение истинности высказывания 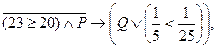
где: P: «Для любого вещественного х выполняется неравенство 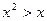 »;
»;
Q: «Существует трапеция с двумя прямыми углами».
3. Упростить формулу: 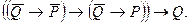
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 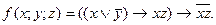
5. Дана функция: 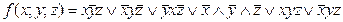
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P(x): «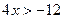 », Q(x): «
», Q(x): «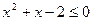 », если:
», если:
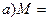 R; б)
R; б) 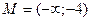 .
.
7. Найти множество истинности предиката, если 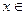 R:
R:
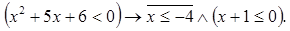 |
XIV вариант
1. Даны множества: 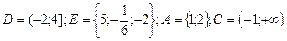
Найти: 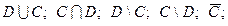
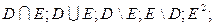 D ∩ N, E \ Z; A ∩ N. Указать все подмножества множества E.
D ∩ N, E \ Z; A ∩ N. Указать все подмножества множества E.
2. Определить значение истинности высказывания 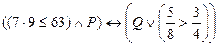 ,
,
где: P: «Существует наибольшее целое отрицательное число»;
Q: «Для любого вещественного х выполняется: 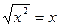 ».
».
3. Упростить формулу: 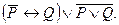
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 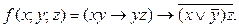
5. Дана функция: 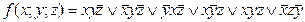
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P(x): «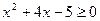 », Q(x): «
», Q(x): «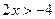 », если:
», если:
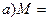 R; б)
R; б) 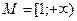 .
.
7. Найти множество истинности предиката, если 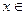 R:
R:
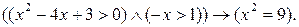
XV вариант
1. Даны множества: 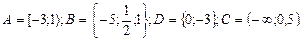
Найти: 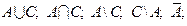
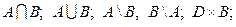 A
A 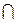 Z; B ∩ N; D
Z; B ∩ N; D 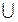 Z.
Z.
Указать все подмножества множества B.
2. Определить значение истинности высказывания 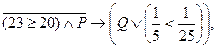
где: P: «Для любого вещественного х выполняется неравенство 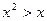 »;
»;
Q: «Существует трапеция с двумя прямыми углами».
3. Упростить формулу: 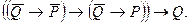
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 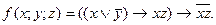
5. Дана функция: 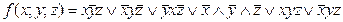
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P(x): «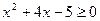 », Q(x): «
», Q(x): «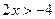 », если:
», если:
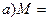 R; б)
R; б) 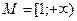 .
.
7. Найти множество истинности предиката, если 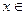 R:
R:
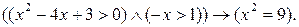
XVI вариант
1. Даны множества: 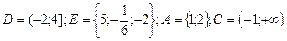
Найти: 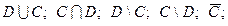
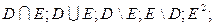 D ∩ N, E \ Z; A ∩ N. Указать все подмножества множества E.
D ∩ N, E \ Z; A ∩ N. Указать все подмножества множества E.
2. Определить значение истинности высказывания 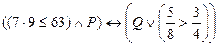 ,
,
где: P: «Существует наибольшее целое отрицательное число»;
Q: «Для любого вещественного х выполняется: 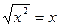 ».
».
3. Упростить формулу: 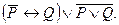
4. Представить булеву функцию в виде СДНФ с помощью равносильных преобразований: 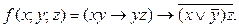
5. Дана функция: 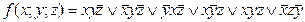
1) задать эту функцию таблично; 2) найти минимальную ДНФ функции методом карт Карно.
6. Выяснить, являются ли данные предикаты равносильными или один является следствием другого на данной области определения:
P(x): «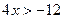 », Q(x): «
», Q(x): «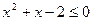 », если:
», если:
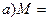 R; б)
R; б) 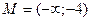 .
.
7. Найти множество истинности предиката, если 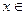 R:
R:
 |
 2015-03-07
2015-03-07 927
927






