Экономический индекс – это относительная величина, получаемая в результате сопоставления уровней социально-экономических явлений во времени, пространстве и с планом. В теории экономических индексов применяется обозначения:
q – количество продукции данного вида в натуральном выражении (физический объем продукции);
p – цена единицы продукции данного вида; 
pq  – стоимость продукции данного вида (товарооборот продукции);
– стоимость продукции данного вида (товарооборот продукции);
z – себестоимость единицы продукции данного вида;
zq – издержки производства;
w – производительность труда;
T – количество отработанного времени;
N – численность работников;
t – трудоемкость продукции.
По степени охвата элементов совокупности различают индивидуальные и общие (сводные) экономические индексы.
Индивидуальные экономические индексы характеризуют изменение изучаемого показателя отдельно по каждому элементу исходной совокупности и обозначаются i с подстрочным знаком индексируемого показателя.
Например, индивидуальный индекс физического объема продукции ( 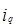 ) вычисляют по формуле
) вычисляют по формуле 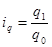 ,
,
где 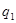 и
и 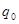 – соответственно, количество продукции в натуральном выражении в отчетном и в базисном периоде.
– соответственно, количество продукции в натуральном выражении в отчетном и в базисном периоде.
Разность числителя и знаменателя соответствующего индивидуального индекса характеризует изменение индексируемого показателя в абсолютном выражении.
Общий (сводный) экономический индекс отражает изменение изучаемого показателя по всем элементам исходной совокупности в целом и обозначается I с соответствующим подстрочным знаком индексируемого показателя. В зависимости от методологии расчета общие (сводные) экономические индексы подразделяются на агрегатные и средние.
Агрегатный индекс физического объема продукции вычисляют по формуле 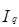 =
= 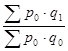 ,
,
где 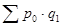 – стоимость всей продукции отчетного периода в базисных ценах;
– стоимость всей продукции отчетного периода в базисных ценах;
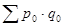 – стоимость всей продукции в базисном периоде.
– стоимость всей продукции в базисном периоде.
Агрегатный индекса цен (индекс Пааше) вычисляют по формуле
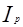 =
= 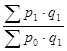 ,
,
где 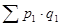 – стоимость всей произведенной (проданной) продукции в отчетном периоде.
– стоимость всей произведенной (проданной) продукции в отчетном периоде.
Кроме индекса Пааше вычисляют общие (сводные) индексы цен по формулам
1) Ласпейреса: 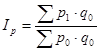 ;
;
2) Фишера: 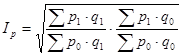 .
.
Общий (сводный) индекс стоимости продукции (товарооборота) вычисляют по формуле 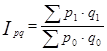 .
.
Между индексами определенных статистических показателей существует такая же взаимосвязь, что и между самими этими показателями, например,
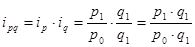 ;
;
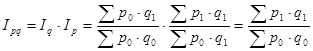 .
.
Пример 1. По одному из магазинов имеются следующие условные данные:
| Вид продукции | Продано продукции, кг | Цена 1 кг, руб. | ||
| январь | март | январь | март | |
| Помидоры | ||||
| Огурцы | ||||
| Апельсины |
Вычислить:
а) индивидуальные и общие индексы: цен, физического объема и стоимости продукции;
б) изменение стоимости всей проданной продукции в марте по сравнению с январем в абсолютном выражении в целом и за счет отдельных факторов.
Решение. Базисным периодом является январь, отчетным – март. Все необходимые величины вычислим в следующей таблице:
| Вид продукции | 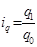
| 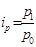
|
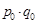
|
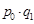
|
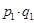
| 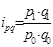
|
| Помидоры | 0,90 | 1,18 | 8 500 | 7 650 | 9 000 | 1,06 |
| Огурцы | 1,20 | 1,10 | 10 000 | 12 000 | 13 200 | 1,32 |
| Апельсины | 1,00 | 1,14 | 6 600 | 6 600 | 7 500 | 1,14 |
| Итого | 25 100 | 26 250 | 29 700 |
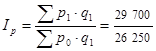 = 1, 13 (113%);
= 1, 13 (113%);
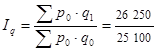 = 1,05 (105%);
= 1,05 (105%);
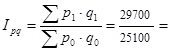 1,18 (118%);
1,18 (118%);
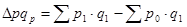 = 29 700 – 26 250 = 3 450 руб.;
= 29 700 – 26 250 = 3 450 руб.;
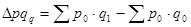 = 26 250 – 25 100 = 1 150 руб.;
= 26 250 – 25 100 = 1 150 руб.;
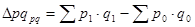 = 29 700 – 25 100 = 4 600 руб.
= 29 700 – 25 100 = 4 600 руб.
Проверим взаимосвязь вычисленных величин
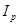 ´
´ 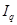 =
= 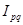 1,13 ´ 1,05 = 1,18;
1,13 ´ 1,05 = 1,18;
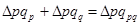 3 450 +1 150 = 4 600 руб.
3 450 +1 150 = 4 600 руб.
Например, индивидуальный индекс цены по помидорам 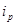 = 1,18 (118%), то это значит, что цена 1 кг проданных помидоров увеличилась в марте по сравнению с январем в 1,18 раза, или на 18% (118% – 100% = 18%).
= 1,18 (118%), то это значит, что цена 1 кг проданных помидоров увеличилась в марте по сравнению с январем в 1,18 раза, или на 18% (118% – 100% = 18%).
Общий индекс физического объема продукции 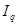 = 1,05. Следовательно, стоимость всей проданной продукции за счет изменения количества продукции в марте по сравнению с январем выросла на 5%. В абсолютном выражении это увеличение составило 1 150 руб. (
= 1,05. Следовательно, стоимость всей проданной продукции за счет изменения количества продукции в марте по сравнению с январем выросла на 5%. В абсолютном выражении это увеличение составило 1 150 руб. (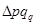 = = 1 150 руб.).
= = 1 150 руб.).
Общий индекс цен 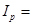 1,13 (113%) и
1,13 (113%) и 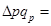 3 450 руб. Значит, стоимость всей проданной продукции за счет изменения уровня цен по каждому виду продукции возросла в марте по сравнению с январем на 13 %, или на 3450 руб.
3 450 руб. Значит, стоимость всей проданной продукции за счет изменения уровня цен по каждому виду продукции возросла в марте по сравнению с январем на 13 %, или на 3450 руб.
Общий индекс стоимости продукции (товарооборота) 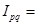 1,18 (118%) и
1,18 (118%) и 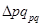 = 4 600 руб. Значит, стоимость всей проданной продукции за счет изменения двух факторов одновременно (цены единицы продукции и физического объема продукции) увеличилась в марте по сравнению с январем на 18%, или на 4 600 руб.
= 4 600 руб. Значит, стоимость всей проданной продукции за счет изменения двух факторов одновременно (цены единицы продукции и физического объема продукции) увеличилась в марте по сравнению с январем на 18%, или на 4 600 руб.
Агрегатный индекс физического объема продукции можно преобразовать в средний арифметический индекс.
Известны по каждому элементу совокупности:
– стоимость продукции в базисном периоде – 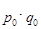 ;
;
– индивидуальные индексы физического объема – 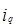 .
.
Из определения 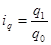 выражаем
выражаем 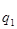 =
= 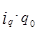 , и подставляем полученное произведение в числитель агрегатного индекса вместо
, и подставляем полученное произведение в числитель агрегатного индекса вместо 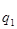
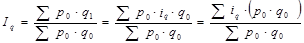 .
.
Получили средний арифметический индекс физического объема продукции.
Пример 2. По одному из магазинов имеются следующие данные:
| Вид продукции | Стоимость продукции, тыс. руб. | Изменение количества проданной продукции в отчетном периоде по сравнению с базисным, % | |
| базисный период | отчетный период | ||
| Мармелад | + 5 | ||
| Зефир | – 15 |
Определить общие индексы физического объема продукции, цен и стоимости продукции.
Решение. Все предварительные расчеты представим в следующей таблице:
| Вид продукции | 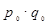
| 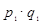
| 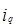
|  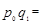 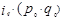
|
| Мармелад | 1,05 | |||
| Зефир | 0,85 | |||
| Итого | – |
Вычислим:
1. Средний арифметический индекс физического объема продукции
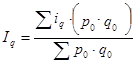 =
= 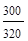 = 0,9375;
= 0,9375;
2. Общий индекс цен 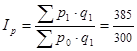 = 1,2833;
= 1,2833;
3. Общий индекс стоимости продукции
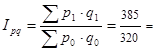 1,2031.
1,2031.
Агрегатный индекс цен Пааше можно преобразовать в средний гармонический индекс.
Известны по каждому элементу совокупности:
– стоимость продукции в отчетном периоде – 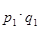 ;
;
– индивидуальные индексы цен – 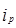 .
.
Из определения 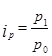 выражаем
выражаем 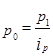 и подставляем полученное выражение в формулу агрегатного индекса цен вместо
и подставляем полученное выражение в формулу агрегатного индекса цен вместо 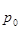 .
.
Получаем средний гармонический индекс цен
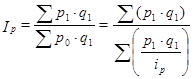 .
.
 2015-03-08
2015-03-08 667
667








