Решение системы из двух нелинейных уравнений.
1. Создать Mat-функции для функций 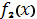 и.
и.
2. Создать файл программы. Ввести текст заглавия задачи, как комментарий. Ввести в него аргументы в заданных пределах.
3. Вывести 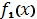 и
и 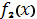 в виде XY графиков. По нему определить приближенно корни системы уравнений, как координаты точек пересечения графиков
в виде XY графиков. По нему определить приближенно корни системы уравнений, как координаты точек пересечения графиков 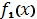 и
и 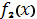 . Если корни на графике не просматриваются, то изменить пределы изменения аргумента и повторить операции.
. Если корни на графике не просматриваются, то изменить пределы изменения аргумента и повторить операции.
4. Для каждого корня найти точное значение, используя функцию fzero к переменной 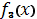 .
.
5. Сформировать строку с результатами и вывести ее в заголовок окна графика.
Варианты заданий сведены в табл. 4.4.
Таблица 4.4
| № | 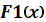 - полином 3- ей степени с коэффициентами - полином 3- ей степени с коэффициентами 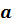
| 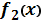
| |||
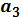
| 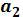
| 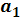
| 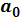
| ||
| -1 | -1 | 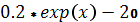
| |||
| -2 | -15 | 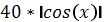
| |||
| -1 | 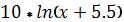
| ||||
| -8 | -70 | 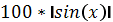
| |||
| -4 | 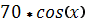
| ||||
| -5 | 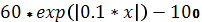
| ||||
| -3 | 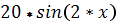
| ||||
| -6 | 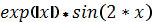
| ||||
| -9 | 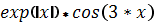
| ||||
| -7 | 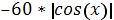
| ||||
| -1 | -4 | 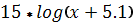
| |||
| -2 | -6 | -7 | 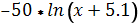
| ||
| -3 | -9 | -8 | 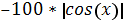
| ||
| -4 | -75 | 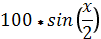
| |||
| -5 | -1 | 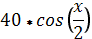
|
|
|
|
 2015-03-20
2015-03-20 326
326








