


 1. Найти произведение матриц:
1. Найти произведение матриц:
| -6 | -7 |
| -8 | -12 | -2 | -6 | ||||||||||||||||||
| -4 | ||||||||||||||||||||||||

| 
| 
| 
| |||||||||||||||||||||
| -3 |
| -2 | -6 | |||||||||||||||||||||
| -5 | -3 | -5 | -1 |
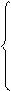 2. Решить системы уравнений:
2. Решить системы уравнений:
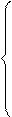
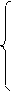 x1 – x2 + x3 = 3, x1 + 2x2 + 3x3 – 2x4 = 6, 2x – 3y + z –2 = 0,
x1 – x2 + x3 = 3, x1 + 2x2 + 3x3 – 2x4 = 6, 2x – 3y + z –2 = 0,
2x1 + x2 + x3 = 11, 2x1 + 4x2 – 2x3 – 3x4 = 18, x + 5y – 4z + 5 = 0,
x1 + x2 + 2x3 = 8. 3x1 + 2x2 – x3 + 2x4 = 4, 4x + y – 3z + 4 = 0.
2x1 – 3x2 + 2x3 + x4 = – 8.
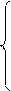
 3x + 2y + z = 5, x – 2y + 3z = 6, 4x – 3y +2z = 9,
3x + 2y + z = 5, x – 2y + 3z = 6, 4x – 3y +2z = 9,
2x + 3y + z = 1, 2x + 3y – 4z = 20, 2x + 5y – 3z = 4,
2x + y + 34z = 11. 3x – 2y – 5z = 6. 5x + 6y – 2z = 18.
 x + y + 2z = – 1, x + y + 2z = – 1, 2x – y – z = 4,
x + y + 2z = – 1, x + y + 2z = – 1, 2x – y – z = 4,
2x – y – 3z = 4, 2x – y + 2z = – 4, 3x + 4y – 2z =11,
5x + 6y – 2z = 18. 4x + y + 4z = – 2. 3x – 2y + 4z = 11.
 3x + 4y + 2z = 8, 4x + 7y – 3z = – 10, – 3x + 6y + 8z = – 7,
3x + 4y + 2z = 8, 4x + 7y – 3z = – 10, – 3x + 6y + 8z = – 7,
2x – y – 3z = – 4, 2x + 9y – z = 8, 9x – 11y – 15z = – 15,
x + 5y + z = 1. x – 6y + 3z = – 3. 18x – 22y + 3z = – 3.


 3. Умножить матрицу на число.
3. Умножить матрицу на число.
| -22 |
| -6 |
| ||||||||||||||||
| -31 |
 2015-04-08
2015-04-08 631
631








