Методы стохастического программирования

Методы используются для задач, в которых все или отдельные параметры описываются с помощью случайных величин. Задачи стохастического программирования возникают тогда, когда каждое действие приводит к неоднозначному исходу и с каждым решением можно связать числовые параметры целевой функции fs(X, Q), s = 0, 1,..., т. При этом параметры fs(X, Q) зависят от конкретного решения X и состояния среды Q. В стохастическом программировании Q является элементарным событием некоторого вероятностного пространства.

Общий подход для решения подобного класса задач заключается в оптимизации некоторой вторичной целевой функции, представляющей собой какую-нибудь стохастическую (вероятностную) характеристику исходной (первичной) функции. В зависимости от вида математической модели (аналитической, вероятностной или статистической), в качестве стохастических характеристик могут использоваться математические ожидания, дисперсии, вероятности либо их оценки. Для неслучайных стохастических характеристик (при известных законах распределения) задача сводится к детерминированной. Если не удается установить аналитическую (формульную) зависимость между параметрами и показателями, то приходится прибегать к методу статистического моделирования (методу Монте-Карло) и с его помощью рассчитывать оценки вторичной целевой функции.

Для решения стохастических задач оптимизации можно использовать градиентные методы, методы стохастического моделирования и стохастической аппроксимации, методы программирования с вероятностными ограничениями.

⃰ ⃰ ⃰

Оптимизация процесса заключается в нахождении оптимума рассматриваемой функции или оптимальных условий проведения данного процесса.

Для оценки оптимума, прежде всего, необходимо выбрать критерий оптимизации. Обычно, критерий оптимизации выбирает из конкретных условий. Это могут быть технологический критерий (например, содержание Сu в отвальном шлаке) или экономический критерий (минимальная стоимость продукта при заданной производительности труда) и др. На основании выбранного критерия оптимизации составляется целевая функция, представляющая собой зависимость критерия оптимизации от параметров влияющих на его значение. Задача оптимизации сводится к нахождению экстремума целевой функции. В зависимости от характера рассматриваемых математических моделей принимаются различные математические методы оптимизации.

Общая постановка задачи оптимизации заключается в следующем:

1. Выбирается критерий

2. Составляется уравнение модели

3. Накладывается система ограничения

4. Решение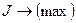

модель 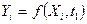- линейная или нелинейная

Ограничения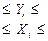

В зависимости от структуры модели применяются различные методы оптимизации. К ним относятся:

1. Аналитические методы оптимизации (аналитический поиск экстремума, метод множителей Лагранжа, Вариационные методы)

2. Математическое программирование (линейное программирование, динамическое программирование)

3. Градиентные методы.

4. Статистические методы (Регрессионный анализ).

Линейное программирование. В задачах линейного программирования критерий оптимальности представляется в виде: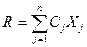

где 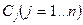- заданные постоянные коэффициенты

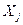- переменные задачи

Уравнения модели представляют собой линейные уравнения (полиномы) вида 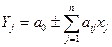на которые накладывается ограничения в виде равенства или неравенства, т.е. 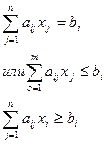(6.2)

В задачах линейного программирования обычно предполагается, что все независимые переменные Х_j неотрицательны, т.е.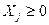

Оптимальным решением задачи линейного программирования является такая совокупность неотрицательных значений независимых переменных

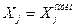
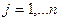, которая удовлетворяет условия (6.2) и обеспечивает в зависимости от постановки задачи max или min значение критерия.

Геометрическая интерпретация (рис.6.7) имеет вид: 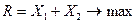- критерий при наличии ограничении на переменных Х₁ и Х₂ типа равенств и неравенств

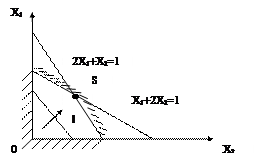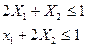
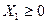
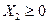
Рис. 6.7

R имеет постоянное значение вдоль линии l. Оптимальное решение будет в точке S, т.к. в этой точке критерий будет max.Одним из методов решения задачи оптимизации линейного программирования является симплекс-метод.

Нелинейное программирование. Математическая постановка задачи нелинейного программирования заключается в следующем: Найти экстремум целевой функции 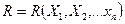, которая имеет вид нелинейности.

На независимые переменные налагаются различные ограничения типа равенств или неравенств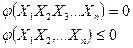

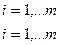
в настоящее время для решения задач нелинейного программирования применяются довольно большое число методов.

К ним относится: 1) Градиентные методы (метод градиента, метод наискорейшего спуска, метод образов, метод Розенброка и т.д.)

2) Безградиентные методы (метод Гауса-Зейделя, метод сканирования).

Градиентные методы оптимизации. Эти методы относятся к численным методам поискового типа. Сущность этих методов заключается в определении значений независимых переменных, дающих наибольшее (наименьшее) изменение целевых функции. Обычно это достигается при движении вдоль градиента, ортогонального к контурной поверхности в данной точке.

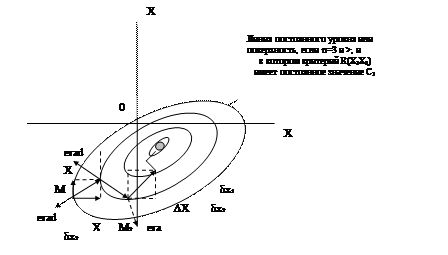Рассмотрим метод градиента. В этом методе используется градиент целевой функции. В методе градиента шаги совершаются в направлении наибыстрейшего уменьшения целевой функции. (Рис. 6.8)

Рис. 6.8 Поиск минимума методом градиента

Поиск оптимума производится в два этапа:

1-этап: - находят значения частных производных по всем независимым переменным, которые определяют направление градиента в рассматриваемой точке.

2-этап: - осуществляется шаг в направлении обратном направлению градиента, т.е. в направлении наибыстрейшего убывания целевой функции.

Алгоритм градиентного метода может быть записан следующим образом:

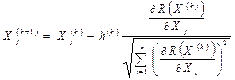(6.3)

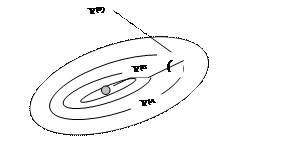Характер движения к оптимуму методом наискорейшего спуска заключается в следующем (рис. 6.9), после того как в начальной точке найден градиент оптимизируемой функции и тем самым определено направление ее наибыстрейшего убывания в указанной точке, в данном направлении делается шаг спуска. Если значение функции в результате этого шага уменьшилась, то производится очередной шаг в том же направлении, и так до тех пор, пока в этом направлении не будет найден минимум, после чего вычисляется снова градиент и определяется новое направление наибыстрейшего убывания целевой функции.

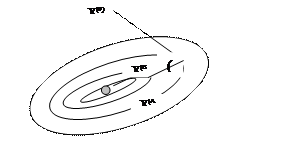
Рис. 6.9

Безградиентные методы поиска экстремума. Эти методы, в отличии от градиентных, используют в процессе поиска информации, получаемую не при анализе производных, а от сравнительной оценки величины критерия оптимальности в результате выполнения очередного шага.

К безградиентным методам поиска экстремума относится:

1. метод золотого сечения

2. метод с использованием чисел Фибония

3. метод Гауса-Зейделя (метод получения изменения переменной)

4. метод сканирования и т.д.