Литература: [8], гл.2, §2, стр. 184–195; [11], гл. 4, § 4.1, стр. 335–348; [27], гл.6, § 57-58, стр. 204-211.
Основные определения, теоремы и формулы
Уравнение (неравенство) или система уравнений (неравенств), которому удовлетворяют координаты любой точки фигуры 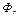 и не удовлетворяют координаты точки, не принадлежащей ей, называется уравнением (неравенством), определяющим фигуру
и не удовлетворяют координаты точки, не принадлежащей ей, называется уравнением (неравенством), определяющим фигуру 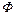 в данной системе координат. Уравнение, определяющее фигуру
в данной системе координат. Уравнение, определяющее фигуру 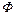 , называют также уравнением фигуры
, называют также уравнением фигуры 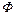 .
.
При выводе уравнения любой фигуры целесообразно действовать в следующей последовательности:
1. Символически записать рассматриваемую фигуру, как множество точек в следующем виде: 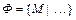 , где вместо многоточия символически записывается характеристическое свойство точек фигуры.
, где вместо многоточия символически записывается характеристическое свойство точек фигуры.
Например, если 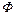 окружность с центром в точке
окружность с центром в точке 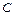 радиуса
радиуса 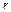 , то следовало бы записать так:
, то следовало бы записать так: 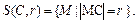
2. Определить, является ли характеристическое свойство аффинным или метрическим.
3. Если свойство является аффинным, то выбирать удобную аффинную систему координат. Если свойство метрическое – прямоугольную систему координат.
4. Считая координаты точки 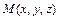 произвольными, записать характеристическое свойство на языке координат. Это и будет уравнением фигуры.
произвольными, записать характеристическое свойство на языке координат. Это и будет уравнением фигуры.
Пример. Описать фигуру, для каждой точки которой сумма квадратов расстояний до трех данных взаимно перпендикулярных прямых постоянна.
Решение. Составим уравнение искомой фигуры 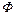 и по виду уравнения определим ее вид.
и по виду уравнения определим ее вид.
Пусть 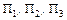 – данные в условии задачи плоскости. Тогда
– данные в условии задачи плоскости. Тогда
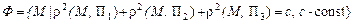 .
.
Характеристическое свойство точек фигуры является метрическим, поэтому необходимо выбрать прямоугольную систему координат. Примем плоскости 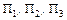 за координатные плоскости
за координатные плоскости 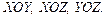 Тогда для точки
Тогда для точки 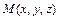 характеристическое свойство примет вид
характеристическое свойство примет вид 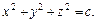 Значит
Значит 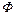 – есть сфера с центром в точке пересечения плоскостей
– есть сфера с центром в точке пересечения плоскостей 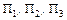 , радиус которой равен
, радиус которой равен 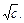
Вопросы для самоконтроля
1. Что называют условием, определяющим фигуру Ф в данной системе координат? Что называется уравнением фигуры Ф?
2. Какая фигура задаётся в прямоугольной декартовой системе координат уравнением:
а) (х – а)2 + (y - b)2 + (z - c)2 = r2, r > 0,
б ) x2 + y2 + z2 + Ax + By + + Cz + D = 0?
3. Фигуры Ф1 и Ф2 имеют в некоторой системе координат уравнения F 1(x, y, z) = 0и F 2(x, y, z) = 0. Какая фигура определяется каждым из следующих условий:
а) F 1(x, y, z) № 0, б) F 1(x, y, z) Ч F 2 (x, y, z) = 0,
в) F 12(x, y, z) + F 22(x, y, z) = 0,
г) системой уравнений F 1(x, y, z) = 0, F 2(x, y, z) = 0, д) 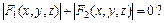
4. Дана аффинная система координат О 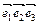 . Написать уравнения её:
. Написать уравнения её:
а) координатных плоскостей, б) координатных осей. Какая фигура определяется уравнением 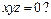
5. Какой вид имеют формулы преобразования аффинных систем координат? Как получить уравнение фигуры Ф в новых координатах 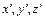 , если известно её уравнение F(x, y, z)= 0 в старой системе координат?
, если известно её уравнение F(x, y, z)= 0 в старой системе координат?
6. Как получить уравнение сферы радиуса r > 0 с центром в начале координат О в декартовой системе координат О 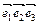 , если известно, что
, если известно, что
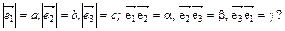
Задачи
1. Какая фигура задаётся уравнением:
а) x2 + y2 + z2 = r2, r > 0;
б) x2 + y2 + z2 – r2 + 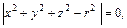
в) х = 0,
г) 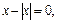 д)
д) 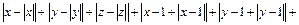
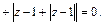
е) x2 + y2 + z2 – 6 x + 8 y + 2 z + 10 = 0?
2. Найти множество всех точек пространства, для каждой из которых:
а) сумма квадратов расстояний до двух данных точек А и В есть постоянная величина с2,
б) разность квадратов расстояний до точек А и В есть постоянная величина с2.
3. Найти множество всех точек пространства, для каждой из которых отношение расстояний до данных точек А и В равно отношению данных отрезков m и n, где m № n.
4. Доказать, что плоскости, проходящие через биссектрисы плоских углов трёхгранного угла перпендикулярно к граням этих углов, пересекаются по одной прямой.
Домашнее задание
1. Найти множество всех точек пространства, каждая из которых равноудалена от двух данных точек А и В.
2. Доказать, что диагональ АС 1 параллелепипеда АВСDA 1 B 1 C 1 D 1 делится плоскостями BDA 1 и B 1 D 1 C на три равные части.
3. Доказать, что сумма квадратов площадей шести диагональных сечений параллелепипеда в два раза больше суммы квадратов площадей всех его граней.
4. Прямая образует равные углы с ребрами трехгранного угла, все плоские углы которого прямые. Найти косинусы этих углов.
5. Доказать, что противоположные ребра правильного тетраэдра взаимно перпендикулярны.
Задачи повышенной трудности
1. Доказать, что все высоты тетраэдра пересекаются в одной точке тогда и только тогда, когда суммы квадратов его противоположных ребер равны.
2. Доказать, что точки 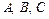 лежат на одной прямой, если их радиус-векторы
лежат на одной прямой, если их радиус-векторы 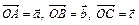 удовлетворяют равенству
удовлетворяют равенству 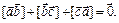
3. Доказать, что грани 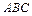 и
и 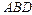 тетраэдра
тетраэдра 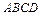 равновелики тогда и только тогда, когда общий перпендикуляр прямых
равновелики тогда и только тогда, когда общий перпендикуляр прямых 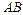 и
и 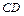 проходит через середину ребра
проходит через середину ребра 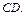
4. Докажите, что плоскость, в которой лежат проекции 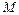 на плоскости координат, делит отрезок, соединяющий
на плоскости координат, делит отрезок, соединяющий 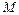 с началом координат, в отношении, не зависящем от положения точки
с началом координат, в отношении, не зависящем от положения точки 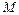 .
.
Тема 5.5. Уравнения плоскости.
 2015-04-12
2015-04-12 1017
1017








