По теме лабораторной работы. В практических вычислениях довольно часто приходится решать уравнения вида

В практических вычислениях довольно часто приходится решать уравнения вида:

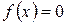, (1)

где функция f(x) определена и непрерывна на некотором конечном или бесконечном интервале .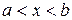

Всякое значение 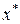, обращающее функцию f(x) в нуль, т. е. такое, что

,

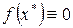называется корнем уравнения (1), а способ нахождения этого значения 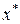и есть решение уравнения (1).

Найти корни уравнения вида (1) точно удается лишь в частных случаях. Кроме того, часто уравнение содержит коэффициенты, известные лишь приблизительно, и, следовательно, сама задача о точном определении корней уравнения теряет смысл. Поэтому разработаны методы численного решения уравнений вида (1), которые позволяют отыскать приближенные значения корней этого уравнения.

При этом приходится решать две задачи:

1) отделение корней, т. е. отыскание достаточно малых областей, в каждой из которых заключен один и только один корень уравнения;

2) вычисление корней с заданной точностью.

При выделении областей, в которых находятся действительные корни уравнения (1), можно воспользоваться тем, что если на концах некоторого отрезка непрерывная функция f(x) принимает значения разных знаков, то на этом отрезке уравнение 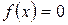имеет хотя бы один корень.

Для выделения областей, содержащих один и только один корень, можно воспользоваться, например, графическим способом.

Для решения второй задачи существуют многочисленные методы, из которых мы рассматриваем лишь один: метод половинного деления.

Пусть известен отрезок 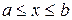, внутри которого существует и располагается один и только один из корней уравнения (1).

Задача состоит в нахождении этого корня.

Метод половинного деления.

Пусть дано уравнение f(x)=0, где функция f(x) непрерывна на отрезке 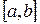и .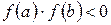

Для нахождения корня уравнения (1), принадлежащего отрезку 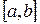, делим отрезок пополам, т. е. выбираем начальное приближение равным 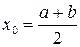. Если f(x₀)=0, то x₀ является корнем уравнения. Если f(x₀)≠0, то выбираем тот из отрезков 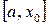или 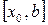, на концах которого функция f(x) имеет противоположные знаки. Полученный отрезок снова делим пополам и проводим то же рассмотрение и т. д.

Процесс деления отрезков пополам продолжаем до тех пор, пока длина отрезка, на концах которого функция имеет противоположные знаки, не будет меньше наперед заданного числа ε.

Пример:

Решить уравнение 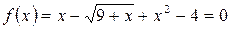с абсолютной погрешностью ε=10^-4, на отрезке [2; 3].

Алгоритм нахождения корня уравнения (2) представляет следующую последовательность действия:

1. Полагаем a=2, b=3 и ε=0,0001.

2. Вычисляем .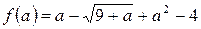

3. Вычисляем 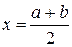и значение функции 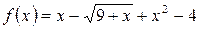в этой точке.

4. Проверяем условие f(x)=0. Если это условие выполняется, то считаем х корнем и заканчиваем вычисления. Если условие не выполняется, то переходим к выбору отрезка, на концах которого функция f(х) имеет разные знаки, а именно:

5. Проверяем условие 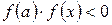. Если это условие выполняется, то полагаем b=x и переходим к п. 6. Если условие не выполняется, то полагаем a=x, f(a)=f(x) и переходим к п. 6.

6. Проверяем условие 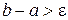. Если оно выполняется, то возвращаемся к процессу деления отрезков пополам, т. е. к п. 3. Если условие не выполняется, т. е. 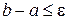, то за результат принимаем значение х и заканчиваем вычисления.

Задания для лабораторной работы:

1. Решить уравнение 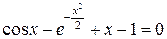с точностью ε=10^-4. Отрезок, содержащий корень: [1; 2].

2. Решить уравнение 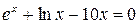с точностью ε=10^-4. Отрезок, содержащий корень: [3; 4].

3. Решить уравнение 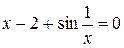с точностью ε=10^-4. Отрезок, содержащий корень: [1,2; 2].

4.Решить уравнение 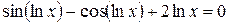с точностью ε=10^-4. Отрезок, содержащий корень: [1; 3].

5. Решить уравнение 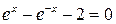с точностью ε=10^-4. Отрезок, содержащий корень: [0; 1].

6.Решить уравнение 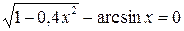с точностью ε=10^-4. Отрезок, содержащий корень: [0; 1].

7.Решить уравнение 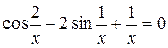с точностью ε=10^-4. Отрезок, содержащий корень: [1; 2].

8. Решить уравнение 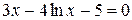с точностью ε=10^-4. Отрезок, содержащий корень: [2; 4].

9. Решить уравнение 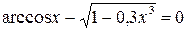с точностью ε=10^-4. Отрезок, содержащий корень: [0; 1].

10. Решить уравнение 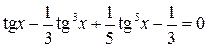с точностью ε=10^-4. Отрезок, содержащий корень: [0; 0,8].

11. Решить уравнение 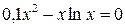с точностью ε=10^-4. Отрезок, содержащий корень: [1; 2].

12. Решить уравнение 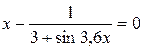с точностью ε=10^-4. Отрезок, содержащий корень: [0; 0,85].

13. Решить уравнение 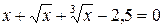с точностью ε=10^-4. Отрезок, содержащий корень: [0,4; 1].

14. Решить уравнение 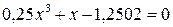с точностью ε=10^-4. Отрезок, содержащий корень: [0; 2].

15. Решить уравнение 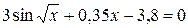с точностью ε=10^-4. Отрезок, содержащий корень: [2; 3].

16. Решить уравнение 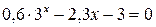с точностью ε=10^-4. Отрезок, содержащий корень: [2; 3].

17. Решить уравнение 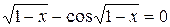с точностью ε=10^-4. Отрезок, содержащий корень: [0; 1].

18. Решить уравнение 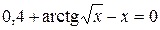с точностью ε=10^-4. Отрезок, содержащий корень: [1; 2].

19. Решить уравнение 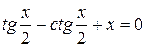с точностью ε=10^-4. Отрезок, содержащий корень: [1; 2].

20. Решить уравнение 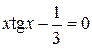с точностью ε=10^-4. Отрезок, содержащий корень: [0,2; 1].

21. Решить уравнение 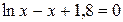с точностью ε=10^-4. Отрезок, содержащий корень: [2; 3].

22. Решить уравнение 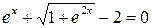с точностью ε=10^-4. Отрезок, содержащий корень: [-1; 0].

23. Решить уравнение 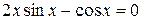с точностью ε=10^-4. Отрезок, содержащий корень: [0,4; 1].

24. Решить уравнение 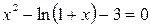с точностью ε=10^-4. Отрезок, содержащий корень: [2; 3].

25. Решить уравнение 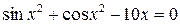с точностью ε=10^-4. Отрезок, содержащий корень: [0; 1].

26. Решить уравнение 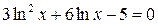с точностью ε=10^-4. Отрезок, содержащий корень: [1; 3].

27. Решить уравнение 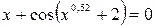с точностью ε=10^-4. Отрезок, содержащий корень: [0,5; 1].

28. Решить уравнение 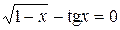с точностью ε=10^-4. Отрезок, содержащий корень: [0; 1].

29. Решить уравнение 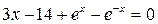с точностью ε=10^-4. Отрезок, содержащий корень: [1; 3].

30. Решить уравнение 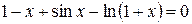с точностью ε=10^-4. Отрезок, содержащий корень: [0; 1,5].

Контрольные вопросы:

1. В чем суть приведенного метода?

2. В чем преимущества данного метода перед другими?

3. В чем суть метода Ньютона?

4. В чем суть метода итераций?

5. Привести примеры методов численного решения.