Приведите уравнение кривой второго порядка к каноническому виду, постройте эту кривую на плоскости и определите основные характеристики этой кривой (для эллипса – длины полуосей, координаты центра, координаты фокусов и координаты вершин; для гиперболы - длины полуосей, координаты центра, координаты фокусов, координаты вершин уравнения асимптот; для параболы - координаты вершины, координату фокуса и уравнение директрисы).
8.1.
a) 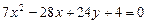 .
.
b) 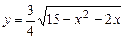 .
.
c) 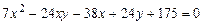 .
.
8.2.
а) 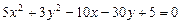 .
.
b) 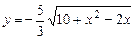 .
.
c) 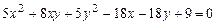 .
.
8.3.
a) 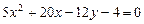 .
.
b) 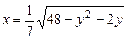 .
.
c) 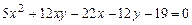 .
.
8.4.
a) 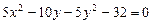 .
.
b) 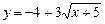 .
.
c) 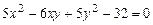 .
.
8.5.
a) 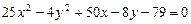 .
.
b) 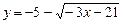 .
.
c) 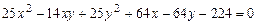
8.6.
a) 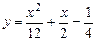 .
.
b) 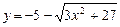 .
.
c) 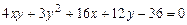 .
.
8.7.
a) 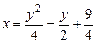 .
.
b) 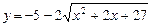 .
.
c) 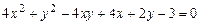 .
.
8.8.
a) 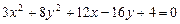 .
.
b) 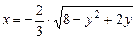 .
.
c) 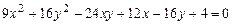 .
.
8.9.
a) 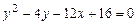 .
.
b) 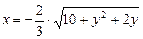 .
.
c) 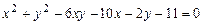 .
.
8.10.
a) 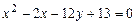 .
.
b) 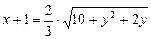 .
.
c) 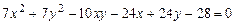 .
.
8.11.
a) 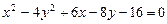 .
.
b) 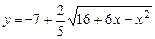 .
.
c) 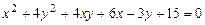 .
.
8.12.
a) 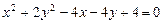 .
.
b) 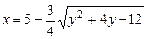 .
.
c) 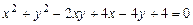 .
.
8.13.
a) 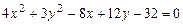 .
.
b) 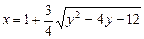 .
.
c) 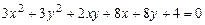 .
.
8.14.
a) 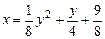 .
.
b) 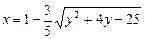 .
.
c) 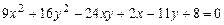 .
.
8.15.
a) 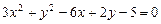 .
.
b) 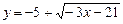 .
.
c) 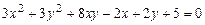 .
.
8.16.
a) 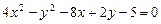 .
.
b) 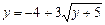 .
.
c) 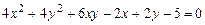 .
.
8.17.
a) 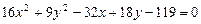 .
.
b) 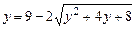 .
.
c) 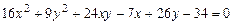 .
.
8.18.
a) 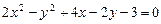 .
.
b) 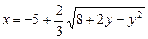 .
.
c) 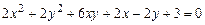 .
.
8.19.
a) 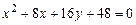 .
.
b) 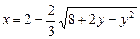 .
.
c) 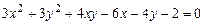
8.20.
a) 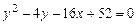 .
.
b) 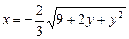 .
.
c) 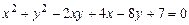 .
.
8.21.
a) 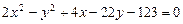 .
.
b) 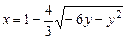 .
.
c) 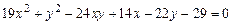 .
.
8.22.
a) 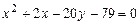 .
.
b) 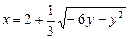 .
.
c) 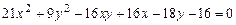 .
.
8.23.
a) 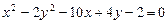 .
.
b) 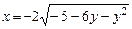 .
.
c) 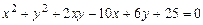 .
.
8.24.
a) 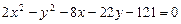 .
.
b) 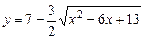 .
.
c) 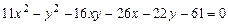 .
.
8.25.
a) 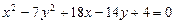 .
.
b) 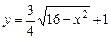 .
.
c) 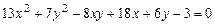 .
.
8.26.
a) 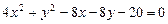 .
.
b) 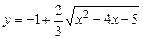 .
.
c) 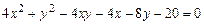 .
.
8.27.
a) 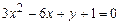 .
.
b) 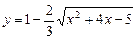 .
.
c) 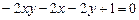 .
.
8.28.
a) 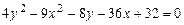 .
.
b) 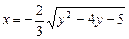 .
.
c) 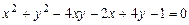 .
.
8.29.
a) 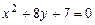 .
.
b) 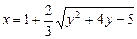 .
.
c) 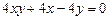 .
.
8.30.
a) 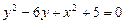 .
.
b) 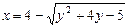 .
.
c) 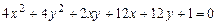 .
.
 2015-04-12
2015-04-12 166
166







