к 4 = 4 + 5 + 6 + 7 = 0 + 1 + 1 + 1 = 1
к2 = 2 + 3 + 6 + 7 = 0 + 1 + 1 + 1 = 1
к1 = 1 + 3 + 5 + 7 = 1 + 1 + 1 + 1 + 0
K= 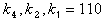 - в шестом разряде ошибка.
- в шестом разряде ошибка.
Если бы нам понадобилось построить код и для проверки двойных ошибок, необходимо было бы ввести еще один дополнительный нулевой разряд.
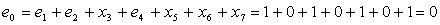
Получим следующий код
0 1 2 3 4 5 6 7
0 1 0 1 0 1 0 1
При передаче и возникновении ошибки код будет иметь вид
0 1 2 3 4 5 6 7
0 1 0 1 0 1 1 1
Проверка в этом случае показала бы, что корректор K=110, а проверка всей комбинации на четность E0 = 0+1+0+1+0+1+1+1=1. Это указывает на одиночную ошибку. Допускается автоматическое исправление ошибки.
Существует следующий алгоритм декодирования кода Хэмминга с d=4
| Корректор - K | Значение E0 | Вывод |
| K=0 | E0=0 | Ошибок нет |
| K#0 | E0#0 | Произошла одиночная ошибка |
| K#0 | E0=0 | Произошла двойная ошибка. Исправление запрещено. |
| K=0 | E0#0 | Произошла тройная или более нечетная ошибка |
Код (7,4) является минимально возможным кодом с достаточно большой избыточностью. Эффективность кода (k/n) растет с увеличением длины кода
| Длина кода - n | ||||
| Число информационных разрядов - k | ||||
| Число контрольных разрядов - r | ||||
| Эффективность кода k/n | 0,57 | 0,73 | 0,84 | 0,9 |
 2015-04-17
2015-04-17 475
475







