Кафедра математики
МАТЕМАТИКА
Задания для контрольных работ студентов-заочников инженерного факультета и методические указания к их решению. Часть II
Тверь – Сахарово 2006
Составитель: доцент кафедры математики Тверской Государственной сельскохозяйственной академии Рятин А.Г.
Рецензент – зав. кафедрой ВТ и МАС, д.т.н., профессор Гриднев В.Р.
Методические указания одобрены на заседании кафедры математики от 16 мая 2006 года.
Утверждены на заседании методической комиссии инженерного факультета от _________ протокол №__
В работе составлены задания к трем контрольным работам для студентов-заочников инженерного факультета по темам: дифференциальное и интегральное исчисления функций многих переменных, числовые и функциональные ряды, обыкновенные дифференциальные уравнения, теория вероятностей. Для каждого задания подробно решена типовая задача.
При выполнении контрольной работы студент выбирает тот вариант, который совпадает с последней цифрой его учебного шифра. При этом, если предпоследняя цифра шифра есть число нечетное (1, 3, 5, 7, 9), то номера задач для соответствующего варианта даны в таблице 1, если эта цифра есть четное число (2, 4, 6, 8, 0), то номера задач даны в таблице 2.
Таблица 1
| Номер варианта | Номера задач | ||
| Работа 4 | Работа 5 | Работа 6 | |
| 1 21 41 61 2 22 42 62 3 23 43 63 4 24 44 64 5 25 45 65 6 26 46 66 7 27 47 67 8 28 48 68 9 29 49 69 10 30 50 70 | 1 21 41 61 81 101 2 22 42 62 82 102 3 23 43 63 83 103 4 24 44 64 84 104 5 25 45 65 85 105 6 26 46 66 86 106 7 27 47 67 87 107 8 28 48 68 88 108 9 29 49 69 89 109 10 30 50 70 90 110 | 1 21 41 61 81 2 22 42 62 82 3 23 43 63 83 4 24 44 64 84 5 25 45 65 85 6 26 46 66 86 7 27 47 67 87 8 28 48 68 88 9 29 49 69 89 10 30 50 70 90 |
Таблица 2
| Номер варианта | Номера задач | ||
| Работа 4 | Работа 5 | Работа 6 | |
| 11 31 51 71 12 32 52 72 13 33 53 73 14 34 54 74 15 35 55 75 16 36 56 76 17 37 57 77 18 38 58 78 19 39 59 79 20 40 60 80 | 11 31 51 71 91 111 12 32 52 72 92 112 13 33 53 73 93 113 14 34 54 74 94 114 15 35 55 75 95 115 16 36 56 76 96 116 17 37 57 77 97 117 18 38 58 78 98 118 19 39 59 79 99 119 20 40 60 80 100 120 | 11 31 51 71 91 12 32 52 72 92 13 33 53 73 93 14 34 54 74 94 15 35 55 75 95 16 36 56 76 96 17 37 57 77 97 18 38 58 78 98 19 39 59 79 99 20 40 60 80 100 |
Контрольная работа №4
В задачах 1 – 20 данную функцию 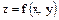 исследовать на экстремум.
исследовать на экстремум.
1. 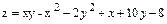 .
.
2. 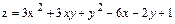 .
.
3. 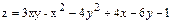 .
.
4. 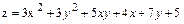 .
.
5. 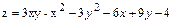 .
.
6. 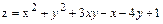 .
.
7. 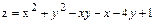 .
.
8. 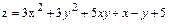 .
.
9. 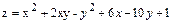 .
.
10. 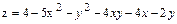 .
.
11. 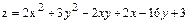 .
.
12. 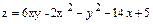 .
.
13. 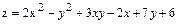 .
.
14. 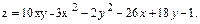
15. 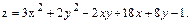
16. 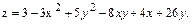
17. 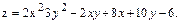
18. 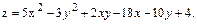
19. 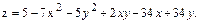
20. 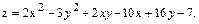
Решение типового примера. Исследовать на экстремум функцию 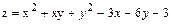 .
.
Решение. Точками экстремума (точками максимума или минимума) могут быть лишь критические точки. Имеем, 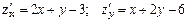 . Так как частные производные существуют, то критические точки найдем из системы уравнений:
. Так как частные производные существуют, то критические точки найдем из системы уравнений: 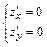 или
или 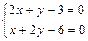 откуда
откуда 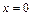 ;
; 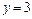 . Найденную критическую точку
. Найденную критическую точку 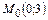 проверим на экстремум. Для этого найдем три числа
проверим на экстремум. Для этого найдем три числа 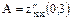 ;
; 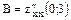 ;
; 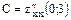 . Если определитель
. Если определитель 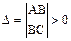 , то в (·) (0;3) имеется экстремум, причем, если А>0, то минимум, если А<0, то максимум. Имеем,
, то в (·) (0;3) имеется экстремум, причем, если А>0, то минимум, если А<0, то максимум. Имеем, 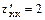 ,
, 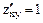 ,
, 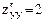 . Поэтому А=2; В=1; С=2 и
. Поэтому А=2; В=1; С=2 и 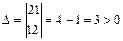 . Значит в (·) (0;3) имеется экстремум и т.к. А=2>0, то минимум. Получаем,
. Значит в (·) (0;3) имеется экстремум и т.к. А=2>0, то минимум. Получаем, 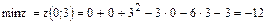 .
.
В задачах 21 – 40 требуется: 1) построить на плоскости хоу область интегрирования заданного интервала; 2) изменить порядок интегрирования и вычислить площадь области при заданном и измененном порядках интегрирования.
21. 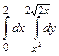 .
.
22. 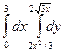 .
.
23. 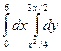 .
.
24. 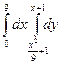 .
.
25. 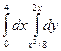 .
.
26. 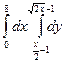 .
.
27. 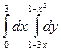 .
.
28. 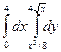 .
.
29. 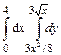 .
.
30. 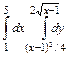 .
.
31. 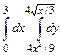 .
.
32. 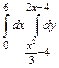 .
.
33. 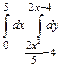 .
.
34. 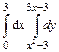 .
.
35. 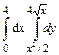 .
.
36. 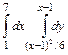 .
.
37. 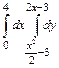 .
.
38. 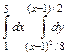 .
.
39. 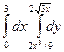 .
.
40. 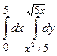
Решение типового примера. Дан повторный интеграл 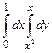 . 1) построить на плоскости область интегрирования D заданного интеграла; 2) изменить порядок интегрирования и вычислить площадь области D при заданном и измененном порядках интегрирования.
. 1) построить на плоскости область интегрирования D заданного интеграла; 2) изменить порядок интегрирования и вычислить площадь области D при заданном и измененном порядках интегрирования.
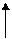
 Решение задачи. Пределы внутреннего интеграла показывают, что область D ограничена сверху линией y=x а снизу y=x2. Пределы внешнего интеграла показывают что данные функции определены на отрезке [0;1]. Поэтому область D имеет вид
Решение задачи. Пределы внутреннего интеграла показывают, что область D ограничена сверху линией y=x а снизу y=x2. Пределы внешнего интеграла показывают что данные функции определены на отрезке [0;1]. Поэтому область D имеет вид
 При изменении порядка интегрирования переменная у меняется на отрезке [0;1], а область D ограничена справа функцией
При изменении порядка интегрирования переменная у меняется на отрезке [0;1], а область D ограничена справа функцией 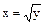 , а слева х=у. Мы получаем
, а слева х=у. Мы получаем 
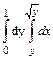 . Вычисляем площадь области D при заданном порядке интегрировании
. Вычисляем площадь области D при заданном порядке интегрировании 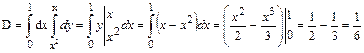 При измененном порядке интегрировании получим
При измененном порядке интегрировании получим 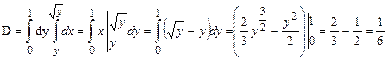
В задачах 41 – 60 вычислить объем тела, ограниченного указанными поверхностями. Данное тело и область интегрирования изобразить на чертеже.
41. 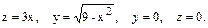
42. 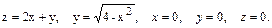
43. 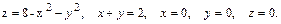
44. 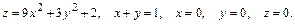
45. 
46. 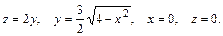
47. 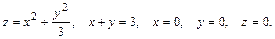
48. 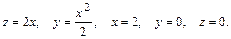
49. 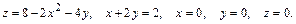
50. 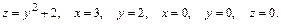
51. 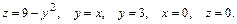
52. 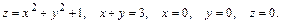
53. 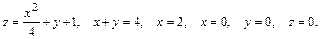
54. 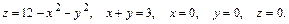
55. 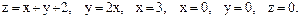
56. 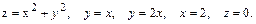
57. 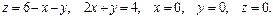
58. 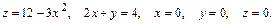
59. 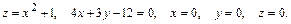
60. 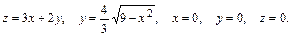
Решение типового примера. Вычислить объем тела, ограниченного плоскостями координат (х=0; у=0; z=0), плоскостями х=4; у=4 и параболоидом вращения 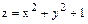 . Решение. Из условия задачи видно, что тело ограничено снизу на плоскости z=0 квадратом со стороной а=4. Сверху тело ограничено поверхностью
. Решение. Из условия задачи видно, что тело ограничено снизу на плоскости z=0 квадратом со стороной а=4. Сверху тело ограничено поверхностью 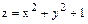 . Поэтому его объем
. Поэтому его объем 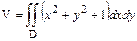 , где область D – квадрат:
, где область D – квадрат: 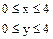 ,. Поэтому
,. Поэтому 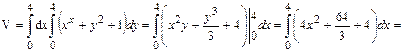
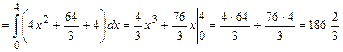
В задачах 61 – 80 даны криволинейный интеграл 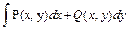 и четыре точки плоскости хоу: О(0,0), А(4,0), В(0,8), С(4,8). Вычислить данный интеграл от точки О до точки С по трем различным путям: 1) по ломанной ОАС; 2) по ломанной ОВС; 3) по дуге ОС параболы
и четыре точки плоскости хоу: О(0,0), А(4,0), В(0,8), С(4,8). Вычислить данный интеграл от точки О до точки С по трем различным путям: 1) по ломанной ОАС; 2) по ломанной ОВС; 3) по дуге ОС параболы 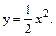 Полученные результаты сравнить и объяснить их совпадение.
Полученные результаты сравнить и объяснить их совпадение.
61. 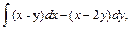
62. 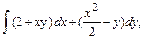
63. 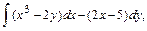
64. 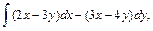
65. 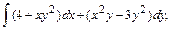
66. 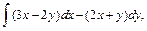
67. 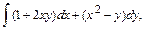
68. 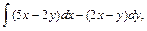
69. 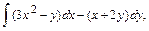
70. 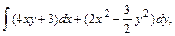
71. 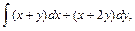
72. 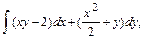
73. 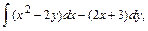
74. 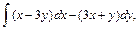
75. 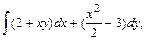
76. 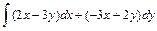
77. 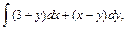
78. 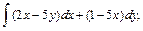
79. 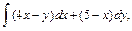
80. 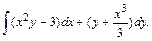
Решение типового примера. Дан криволинейный интеграл 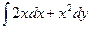 и четыре точки плоскости хоу: О (0;0), А (4;0), В (0;8), С (4;8). Вычислить данный интеграл по трем различным путям: 1) по ломанной ОАС, 2) по ломанной ОВС, 3) по дуге ОС параболы
и четыре точки плоскости хоу: О (0;0), А (4;0), В (0;8), С (4;8). Вычислить данный интеграл по трем различным путям: 1) по ломанной ОАС, 2) по ломанной ОВС, 3) по дуге ОС параболы 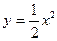 . Полученные результаты сравнить и объяснить их совпадение.
. Полученные результаты сравнить и объяснить их совпадение.
Решение задачи: 1) 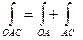 . Вычислим
. Вычислим 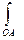 . Уравнение отрезка ОА: у=0;
. Уравнение отрезка ОА: у=0; 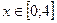 тогда dy=0 и
тогда dy=0 и 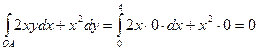 . Далее уравнение АС: х=4;
. Далее уравнение АС: х=4; 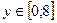 . Тогда dx=0 и
. Тогда dx=0 и 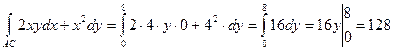 Поэтому
Поэтому 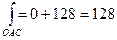
2) 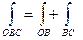 . Вычислим
. Вычислим 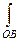 . Уравнение отрезка ОВ: х=0;
. Уравнение отрезка ОВ: х=0; 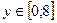 . Поскольку dx=0 и
. Поскольку dx=0 и 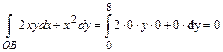 . Далее, уравнение ВС: у=8;
. Далее, уравнение ВС: у=8; 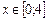 . Тогда dy=0 и
. Тогда dy=0 и 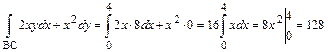 . Поэтому
. Поэтому 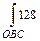 .
.
3) Вычислим интеграл по дуге параболы: 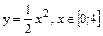 , тогда dy=xdx и
, тогда dy=xdx и 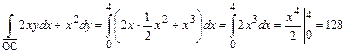
Вывод: по всем трем путям, соединяющим точки О(0;0) и С(4;8) интеграл одинаков. Здесь в интеграле 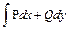 функции Р=2xy, Q=
функции Р=2xy, Q= 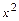 и
и 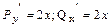 удовлетворяют условию независимости интеграла от пути интегрирования:
удовлетворяют условию независимости интеграла от пути интегрирования: 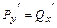 .
.
Контрольная работа № 5.
В задачах 1 – 20 найти частное решение дифференциального уравнения, удовлетворяющее указанному начальному условию.
1. 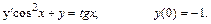
2. 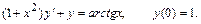
3. 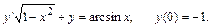
4. 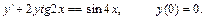
5. 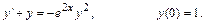
6. 
7. 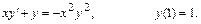
8. 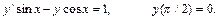
9. 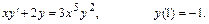
10. 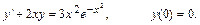
11. 
12. 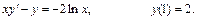
13. 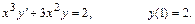
14. 
15. 
16. 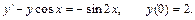
17. 
18. 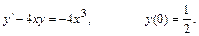
19. 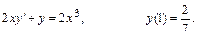
20. 
Решение типового примера. Найти частное решение дифференциального уравнения 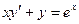 , удовлетворяющее данному условию у(1)=е.
, удовлетворяющее данному условию у(1)=е.
Решение. Данное уравнение является линейным и его можно решить с помощью подстановки Бернулли. Положим, y=uv. Тогда 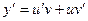 . Подставим в исходное уравнение. Получим,
. Подставим в исходное уравнение. Получим, 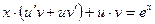 или
или 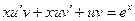 или
или 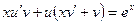 . Потребуем, чтобы выполнялось равенство
. Потребуем, чтобы выполнялось равенство 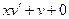 , т.е.
, т.е. 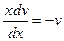 или
или 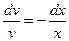 или, после интегрирования
или, после интегрирования 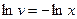 , т.е.
, т.е. 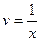 . Для найденного
. Для найденного 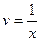 уравнение примет вид
уравнение примет вид 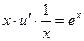 или
или 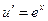 т.е.
т.е. 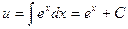 . Значит, общим решением уравнения будет
. Значит, общим решением уравнения будет 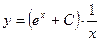 . Подставляя заданное начальное условие у(1)=е, получим e=е+C. Откуда С=0 и нужным частным решением будет
. Подставляя заданное начальное условие у(1)=е, получим e=е+C. Откуда С=0 и нужным частным решением будет 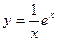 .
.
В задачах 21 – 40 понизить порядок и решить дифференциальное уравнение, удовлетворяющее начальным условиям.
21. 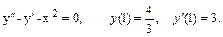
22. 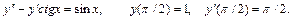
23. 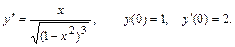
24. 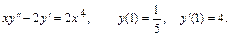
25. 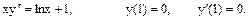
26. 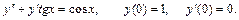
27. 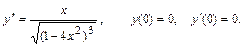
28. 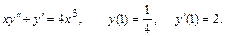
29. 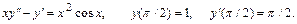
30. 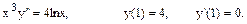
31. 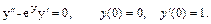
32. 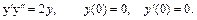
33. 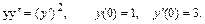
34. 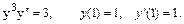
35. 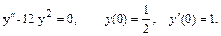
36. 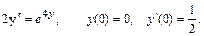
37. 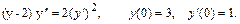
38. 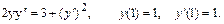
39. 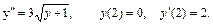
40. 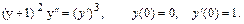

В уравнениях 21 – 30 отсутствует переменная у, т.е. они имеют вид 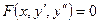 и понизить их порядок можно заменой
и понизить их порядок можно заменой 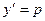 , где р – зависит от х и уравнение примет вид
, где р – зависит от х и уравнение примет вид 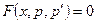 .
.
В уравнениях 31 – 40 отсутствует переменная х, т.е. они имеют вид 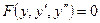 . В этом случае понизить их порядок можно заменой
. В этом случае понизить их порядок можно заменой 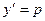 , где р зависит от у и
, где р зависит от у и 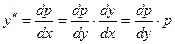 . Например, понизить порядок и решить дифференциальное уравнение
. Например, понизить порядок и решить дифференциальное уравнение 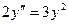 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: 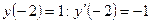 .
.
Решение: пусть 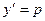 и
и 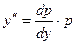 . Тогда
. Тогда  или
или 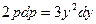 . После интегрирования обеих частей равенства, получим
. После интегрирования обеих частей равенства, получим 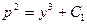 или
или 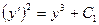 . Подставляя начальные условия, найдем
. Подставляя начальные условия, найдем 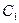 . Получим
. Получим 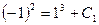 . Откуда
. Откуда 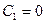 и
и 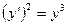 . Т.к. из начальных условий следует, что
. Т.к. из начальных условий следует, что 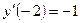 , то из уравнения
, то из уравнения 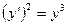 имеем,
имеем, 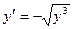 или
или 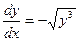 или
или  . После интегрирования, получим
. После интегрирования, получим 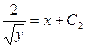 . Подставляя начальные условия, найдем
. Подставляя начальные условия, найдем 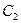 . Имеем
. Имеем 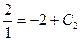 . Откуда
. Откуда 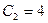 и нужное частное решение имеет вид
и нужное частное решение имеет вид 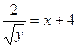 .
.
В задачах 41 – 60 даны линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Найти частное решение, удовлетворяющее указанным начальным условиям.
41. 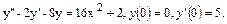
42. 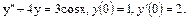
43. 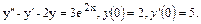
44. 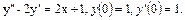
45. 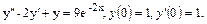
46. 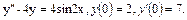
47. 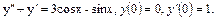
48. 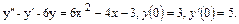
49. 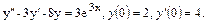
50. 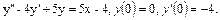
51. 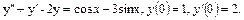
52. 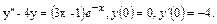
53. 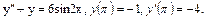
54. 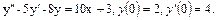
55. 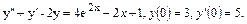
56. 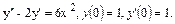
57. 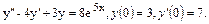
58. 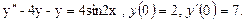
59. 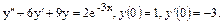
60. 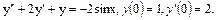
Решение типового примера. Найти частное решение неоднородного дифференциального уравнения с постоянными коэффициентами, удовлетворяющее начальным условиям: 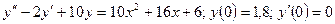 .
.
Решение: для нахождения общего решения исходного уравнения найдем 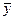 общее решение соответствующего однородного уравнения, а затем
общее решение соответствующего однородного уравнения, а затем 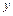 - частное решение исходного уравнения. Общим решением исходного уравнения будет
- частное решение исходного уравнения. Общим решением исходного уравнения будет 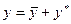 . Составим характеристическое уравнение и найдем его корни. Имеем,
. Составим характеристическое уравнение и найдем его корни. Имеем, 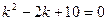 . Откуда,
. Откуда, 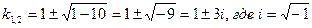 . Поскольку корни характеристического уравнения комплексные числа, то
. Поскольку корни характеристического уравнения комплексные числа, то 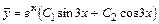 . Частное решение будем искать в виде многочлена
. Частное решение будем искать в виде многочлена 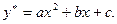 Найдем производные и подставим
Найдем производные и подставим 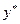 в исходное уравнение. Имеем,
в исходное уравнение. Имеем, 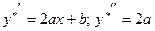 . Значит,
. Значит, 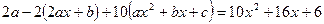 . Или
. Или  . Откуда, приравнивая коэффициенты при х в одинаковых степенях, получим систему уравнений:
. Откуда, приравнивая коэффициенты при х в одинаковых степенях, получим систему уравнений: 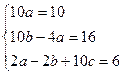 , откуда а=1; b=2; c=0,8.
, откуда а=1; b=2; c=0,8.
Поэтому 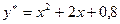 и общим решение будет
и общим решение будет 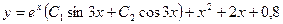 . Для нахождения значений
. Для нахождения значений 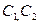 подставим начальные условия
подставим начальные условия 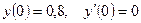 .
.
Получим 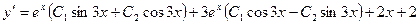
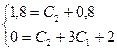 , откуда
, откуда 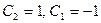 . Нужное частное решение имеет вид
. Нужное частное решение имеет вид 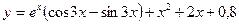 .
.
В задачах 61 – 70 исследовать сходимость рядов, пользуясь признаком сходимости Даламбера.
61. 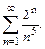
62. 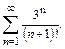
63. 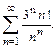
64. 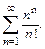
65. 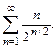
66. 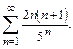
67. 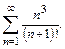
68. 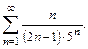
69. 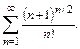
70. 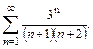
Решение типового примера.
Исследовать на сходимость ряд 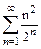 .
.
Решение. Имеем, 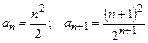 . Найдем
. Найдем 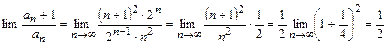
Так как 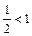 , то по признаку Даламбера ряд сходится.
, то по признаку Даламбера ряд сходится.
В задачах 71 – 80 исследовать сходимость рядов, пользуясь интегральным признаком сходимости Коши.
71. 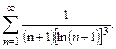
72. 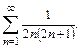
73. 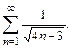
74. 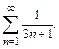
75. 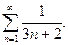
76. 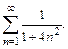
77. 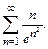
78. 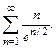
79. 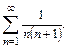
80. 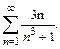
Решение типового примера. Исследовать на сходимость ряд, пользуясь интегральным признаком сходимости. 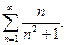
Решение. Здесь общим членом 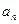 положительного ряда будет
положительного ряда будет 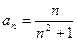 . Рассмотрим функцию
. Рассмотрим функцию 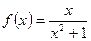 и исследуем на сходимость несобственный интеграл
и исследуем на сходимость несобственный интеграл 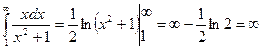 . Так как несобственный интеграл расходится, то и ряд
. Так как несобственный интеграл расходится, то и ряд 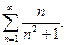 также расходится по интегральному признаку.
также расходится по интегральному признаку.
В задачах 81 – 100 дан степенной ряд
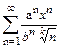
Написать первые четыре члена ряда, найти интервал сходимости ряда и выяснить вопрос о сходимости ряда на концах интервала. Значения a, b и k даны.
81. 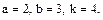
82. 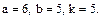
83. 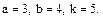
84. 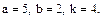
85. 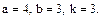
86. 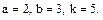
87. 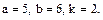
88. 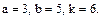
89. 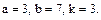
90. 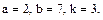
91. 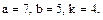
92. 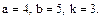
93. 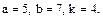
94. 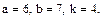
95. 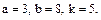
96. 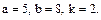
97. 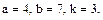
98. 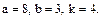
99. 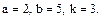
100. 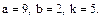
Решение типового примера. Написать четыре члена степенного ряда, найти интервал его сходимости и исследовать вопрос о сходимости ряда на концах интервала. 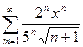 .
.
Решение. Имеем 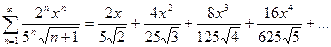
Для нахождения интервала сходимости применим признак Даламбера для соответствующего положительного ряда (в интервале сходимости степенной ряд сходится абсолютно). Имеем, 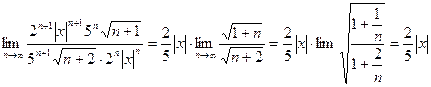 По признаку Даламбера ряд сходится, если
По признаку Даламбера ряд сходится, если 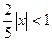 и расходится, если
и расходится, если 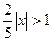 . Значит интервалом сходимости служит
. Значит интервалом сходимости служит 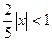 или
или 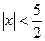 или
или 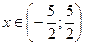 . Исследуем сходимость ряда на концах интервала. Пусть
. Исследуем сходимость ряда на концах интервала. Пусть 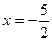 , тогда получаем ряд
, тогда получаем ряд 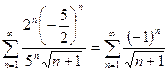 - знакочередующийся ряд сходится по признаку Лейбница (общий член монотонно стремится к нулю). Пусть теперь
- знакочередующийся ряд сходится по признаку Лейбница (общий член монотонно стремится к нулю). Пусть теперь 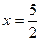 , тогда получаем ряд
, тогда получаем ряд 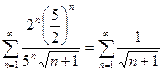 . Исследуем его сходимость с помощью интегрального признака. Для этого исследуем на сходимость несобственный интеграл
. Исследуем его сходимость с помощью интегрального признака. Для этого исследуем на сходимость несобственный интеграл 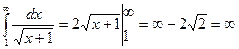 . Так как несобственный интеграл расходится, то и ряд расходится.
. Так как несобственный интеграл расходится, то и ряд расходится.
Ответ: область сходимости ряда: 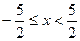
В задачах 101 – 120 требуется вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда.
101. 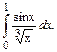
102. 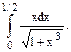
103. 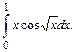
104. 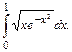
105. 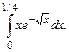
106. 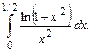
107. 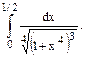
108. 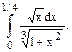
109. 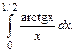
110. 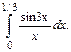
111. 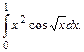
112. 
113. 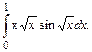
114. 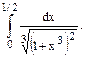
115. 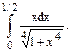
116. 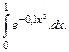
117. 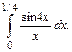
118. 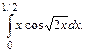
119. 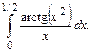
120. 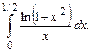
Решение типового примера. Вычислить с точностью до 0,001 интеграл 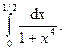
Решение. Разложим подинтегральную функцию в степенной ряд с помощью биномиального ряда 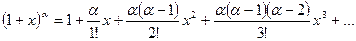 Имеем,
Имеем, 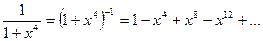 Тогда
Тогда 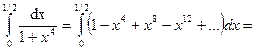
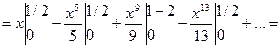
 Мы получили знакочередующийся ряд, третий член которого меньше 0,0003. Поэтому для вычисления его суммы с точностью до 0,001 достаточно взять два его члена. Получаем,
Мы получили знакочередующийся ряд, третий член которого меньше 0,0003. Поэтому для вычисления его суммы с точностью до 0,001 достаточно взять два его члена. Получаем, 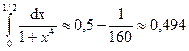 .
.
Контрольная работа №6
В задачах 1 – 20 вычислить вероятность события, используя классическое определение вероятности как долю благоприятных исходов опыта среди всех равновозможных исходов, теоремы сложения и умножения вероятностей, а также формулу полной вероятности.
1. В ящике 100 одинаковых по виду деталей, в т.ч. 80 стандартных и 20 нестандартных. Извлекаются 3 детали. Какова вероятность, что среди них две стандартные?
2. Вероятность попадания в мишень равна 0,8. После первого попадания стрельба прекращается. Найти вероятность того, что будет произведено не менее 4 выстрелов.
3. В урне 4 белых и 6 черных шаров. Наудачу вынуто 5 шаров. Найти вероятность того, что из них два шара белые и три черные.
4. 70 % населения данной местности доживают до 50 лет, из них 40 % доживают до 70 лет. Найти вероятность того, что новорожденный доживет до 70 лет.
5. Среди 6 винтовок пристрелянными являются только 2. Вероятность попадания из пристрелянной винтовки равна 0,9, из непристрелянной – 0,2. Найти вероятность поражения цели из наудачу взятой винтовки.
6. Экспедиция издательства отправила газеты в три почтовых отделения. Вероятность своевременной доставки в первое отделение равна 0,95, во второе – 0,9, в третье – 0,8. Найти вероятность того, что хотя бы одно отделение получит газеты вовремя.
7. Сборщик получил три ящика: в первом ящике 40 деталей, из них 20 окрашенных; во втором – 50, из них 10 окрашенных; в третьем – 30 деталей, из них 15 окрашенных. Найти вероятность того, что наугад извлеченная деталь из наугад взятого ящика окажется окрашенной.
8. В урне 2 белых и 5 черных шаров. Из урны вынимают наудачу два шара. Найти вероятность того, что оба шара будут белыми.
9. На предприятиях брак составляет в среднем 1,5 % от общего выпуска изделий. Среди годных изделий первый сорт составляет 80 %. Какова вероятность того, что наудачу взятое изделие окажется изделием первого сорта, если оно взято из общей массы изготовленной продукции?
10. Из 15 мальчиков и 10 девочек составляется наугад группа из 5 человек. Какова вероятность того, что в нее попадут 3 мальчика и 2 девочки?
11. Стрелок производит 3 выстрела по мишени, вероятность попадания в цель при одном выстреле равна 0,8. Найти вероятность поражения цели хотя бы одним выстрелом.
12. В урне 3 белых и 5 черных шаров. Из урны вынимают наугад 2 шара. Найти вероятность того, что оба шара белые.
13. Три станка работают независимо. Вероятность того, что первый станок в течении смены выйдет из строя равна 0,1, для второго и третьего станков эти вероятности соответственно равны 0,2 и 0,3. Найти вероятность того, что в течении смены хотя бы один станок выйдет из строя.
14. В ящике 12 писем, из них 7 иногородних и 5 городских. Какова вероятность, что среди 5 наугад вынутых писем окажутся 3 иногородних?
15. Три стрелка производят по одному выстрелу по мишени. Вероятность попадания в мишень первым стрелком равна 0,9, вторым – 0,8, третьим – 0,7. Найти вероятность того, что мишень будет поражена.
16. В группе 12 студентов, из них 7 отличников. Из группы взято наудачу 5 человек. Какова вероятность, что среди них окажется 3 отличника?
17. Полный комплект домино содержит 28 костей. Какова вероятность того, что наугад взятая кость содержит 8 очков?
18. Два стрелка делают 2 выстрела по мишени. Для первого стрелка вероятность попадания в цель при одном выстреле равна 0,7, для второго – 0,9. Найти вероятность поражения цели хотя бы одним выстрелом.
19. Рабочий обслуживает три станка, работающих независимо друг от друга. Вероятность того, что в течении часа не потребует внимания рабочего первый станок – 0,9, второй – 0,8, третий – 0,85. Найти вероятность того, что в течении часа, хотябы один станок потребует внимания рабочего.
20. Из трамвайного парка в случайном порядке выходят 4 трамвая №1 и 8 трамваев маршрута №2. Найти вероятность того, что второй из вышедших на линию трамваев будет иметь №1.
Пример решения задачи. В партии 2% бракованных изделий. Среди небракованных изделий 80% изделий высшего сорта из партии наудачу взято изделие. Какова вероятность, что оно первого сорта?
Решение. Пусть А – изделие не бракованное, В – изделие первого сорта. Тогда В=А*В и по теореме умножения вероятностей Р(В)=Р(А)*РА(В). Но, т.к. вероятность брака равна 0,02, то Р(А)=0,98. Далее по условию РА(В)=0,8. Поэтому Р(В)=0,98*0,8=0,784.
В задачах 21 – 40 вычислить вероятность события используя схему повторных независимых испытаний: одно и тоже испытание проводится n раз. В каждом испытании событие А может появится с вероятностью р. Найти вероятность того, что в n испытаниях событие А появится ровно k раз. Задача решается с помощью формулы Бернулли.
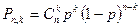 ,
,
где 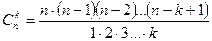 .
.
При этом, если n – велико, то при использовании формулы Бернулли возникают большие трудности вычислительного характера. Для преодоления этих трудностей используют приближенные формулы Пуассона и Лапласа. Формула Пуассона 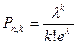 применяется тогда, когда n – велико, а р – мало, т.е. np=
применяется тогда, когда n – велико, а р – мало, т.е. np= 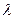 <10.
<10.
В случае, если n – велико, а р – значительное, т.е. p>>10, то формула Пуассона дает большую погрешность и в этом случае пользуются формулой Лапласа:
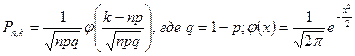 дифференциальная функция Лапласа. Функция
дифференциальная функция Лапласа. Функция 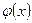 табулирована и ее значения можно найти в соответствующих таблицах. При решении задачи о вероятности того, что в n испытаниях события А появилось не менее k раз и не более
табулирована и ее значения можно найти в соответствующих таблицах. При решении задачи о вероятности того, что в n испытаниях события А появилось не менее k раз и не более 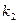 раза используют интегральную функцию Лапласа
раза используют интегральную функцию Лапласа 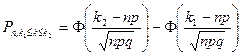 , где
, где
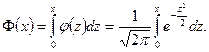
21. Вероятность изготовления стандартной детали равна 0,8. Найти вероятность того, что из 5 изготовленных деталей стандартных будет а) три, б) не менее одной.
22. Вероятность появления бракованной детали равна 0,008. Найти вероятность того, что из 500 случайно отобранных деталей окажется три бракованных.
23. Производятся независимые испытания новых машин, в каждом из которых вероятность появления события А – отказ равна 0,8. Найти вероятность того, что в 100 испытаниях событие А появится более 79 раз.
24. Всхожесть семян данного растения составляет 90 %. Найти вероятность того, что из четырех посеянных семян взойдут: а) три, б) не менее трех.
25. Семена содержат 0,1 % сорняков. Какова вероятность при случайном отборе 2000 семян обнаружить 5 семян сорняков?
26. В хлопке число длинных волокон составляет 80 %. Какова вероятность того, что среди взятых наудачу 5 волокон длинных окажется а) три, б) не более двух.
27. Вероятность выживания бактерий после радиоактивного облучения равна 0,004. Найти вероятность того, что после облучения из 500 бактерий останется не менее 3 бактерий.
28. Вероятность того, что деталь выточенная на станке-автомате окажется первого сорта равна 0,8. Найти вероятность того, что из 100 выточенных деталей первого сорта окажется не менее 72 и не более 84.
29. Прибор состоит из 4 узлов. Вероятность безотказной работы в течении смены для каждого узла равна 0,8. Узлы выходят из строя независимо один от другого. Найти вероятность того, что за смену откажут: а) два узла, б) не менее двух узлов.
30. Производятся независимые испытания, в каждом из которых вероятность появления события А равна 0,8. Найти вероятность того, что в 100 испытаниях событие А появится: а) ровно 90 раз, б) не менее 90 раз, в) менее 90 раз.
31. Принимая вероятность рождения мальчика и девочки одинаковыми, найти вероятность того, что среди 6 новорожденных а) 4 мальчика, б) не более двух девочек.
32. Вероятность отказа агрегата при одном испытании равна 0,8. найти вероятность того, что при 100 испытаниях агрегат откажет более 70 раз.
33. Производятся 5 независимых испытаний, в каждом из которых вероятность появления события А равна 0,1. Найти вероятность того, что событие А появится а) 2 раза, б) не менее 4 раз, в) менее 4 раз.
34. Для оценки надежности узла проводятся 5 независимых испытаний. Вероятность его отказа при одном испытании равна 0,4. Найти вероятность того, что узел откажет не менее трех раз.
35. Производятся независимые испытания, в каждом из которых вероятность появления события А равна 0,2. Найти вероятность того, что в 100 испытаниях событие А появится: а) ровно 20 раз, б) более 20 раз, в) не более 20 раз.
36. В некотором водоеме карпы составляют 80 %. Найти вероятность того, что из 5 выловленных в этом водоеме рыб окажется: а) 4 карпа, б) не менее 4 карпов.
37. На склад поступают изделия, из которых 80 % оказываются высшего сорта. Найти вероятность того, что из 100 взятых изделий не менее 85 изделий окажутся высшего сорта.
38. Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течении часа равна 0,002. Найти вероятность того, что за час откажут 4 элемента.
39. Книга издана тиражом в 50000 экземпляров. Вероятность того, что в книге имеется дефект брошюровки, равна 0,0001. Найти вероятность того, что тираж содержит 5 неправильно сброшюрованных книг.
40. Доля бракованных деталей, выпускаемых станком-автоматом, составляет 25 %. Наудачу взято 6 деталей. Найти вероятность того, что среди взятых деталей будет: а) ровно 5 бракованных, б) не более 5 бракованных.
Пример решения задачи. Вероятность появления события А в каждом из 625 испытаниях равна 0,64. Найти вероятность того, что событие А в этих испытаниях появится ровно 415 раз. Здесь n=625 – велико, а р=0,64 значительно, т.е. 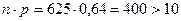 . Поэтому для решения задачи мы воспользуемся формулой Лапласа. Имеем, n=625, p=0,64, np=625*0,64=400, npq=625*0,64*0,36=144,
. Поэтому для решения задачи мы воспользуемся формулой Лапласа. Имеем, n=625, p=0,64, np=625*0,64=400, npq=625*0,64*0,36=144, 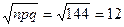 . По формуле Лапласа имеем,
. По формуле Лапласа имеем, 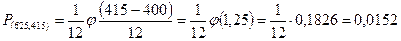
В задачах 41 – 60 задан закон распределения случайной величины Х (в первой строке таблицы даны возможные значения величины Х, а во второй строке указаны вероятности р этих возможных значений).
Найти: 1) математическое ожидание М(Х); 2) дисперсию D(Х); 3) среднее квадратическое отклонение s.
41. 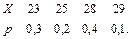
42. 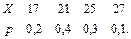
43. 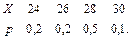
44. 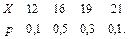
45. 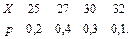
46. 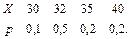
47. 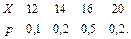
48. 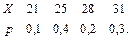
49. 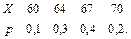
50. 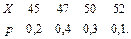
51. 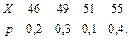
52. 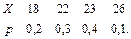
53. 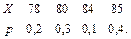
54. 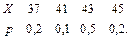
55. 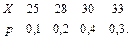
56. 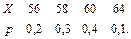
57. 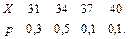
58. 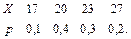
59. 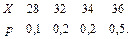
60. 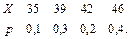
Пример решения типовой задачи. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение дискретной случайной величины, заданной рядом распределения.
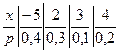
Решение. Математическое ожидание дискретной случайной величины находится по формуле 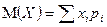 . В нашем случае
. В нашем случае 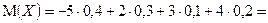
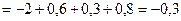
Дисперсия находится по формуле: 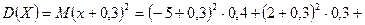
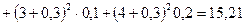
Среднее квадратическое отклонение 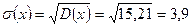 .
.
В задачах 61 – 80 случайная величина Х задана интегральной функцией распределения F(x). Найти: 1) дифференциальную функцию распределения f(x); 2) математическое ожидание М (х); 3) дисперсию D(Х).
61. 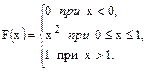
62. 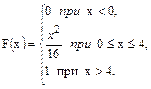
63. 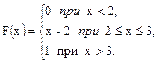
64. 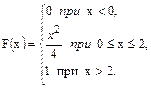
65. 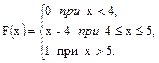
66. 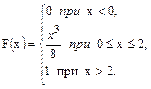
67. 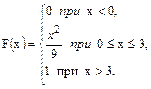
68. 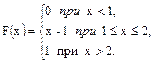
69. 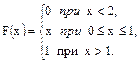
70. 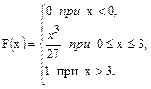
71. 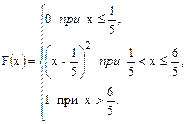
72. 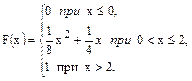
73. 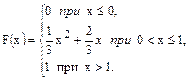
74. 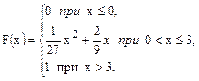
75. 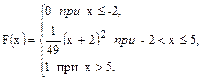
76. 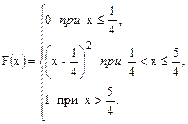
77. 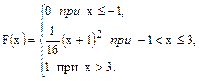
78. 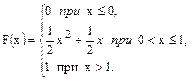
79. 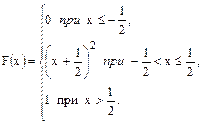
80. 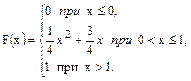
Пример решения типовой задачи. Случайная величина Х задана интегральной функцией распределения
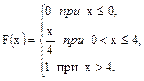
Найдем: 1) дифференциальную функцию распределения f(x), 2) математическое ожидание М(Х), 3) дисперсию D(X).
Решение. Найти дифференциальную функцию f(x)
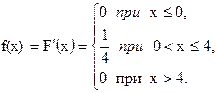
Математическое ожидание Х найдем по формуле: 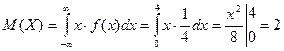
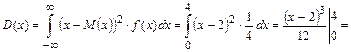
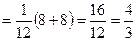 .
.
В задачах 81 – 100 дано, что детали, выпускаемые цехом, по размеру диаметра распределены по нормальному закону. Стандартная длина диаметра детали (математическое ожидание) равна a мм, среднее квадратическое отклонение - s мм. Найти: 1) вероятность того, что диаметр наудачу взятой детали будет больше a мм и меньше b мм; 2) вероятность того, что диаметр детали отклонится от стандартной длины не более чем на d мм. Значения a, s, a, b, d даны.
81. 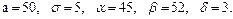
82. 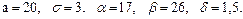
83. 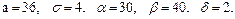
84. 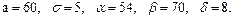
85. 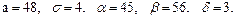
86. 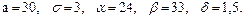
87. 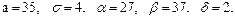
88. 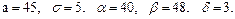
89. 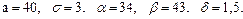
90. 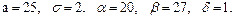
91. 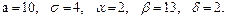
92. 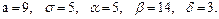
93. 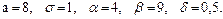
94. 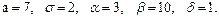
95. 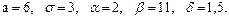
96. 
97. 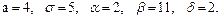
98. 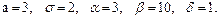
99. 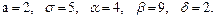
100. 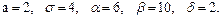
Решение типовой задачи. Заданы математическое ожидание a и среднее квадратическое отклонение σ нормально распределенной случайной величины 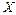 . Найти: 1) вероятность того, что Х примет значение принадлежащее интервалу (α;β), 2) вероятность того, что абсолютная величина отклонения Х – а окажется меньше σ.
. Найти: 1) вероятность того, что Х примет значение принадлежащее интервалу (α;β), 2) вероятность того, что абсолютная величина отклонения Х – а окажется меньше σ.
Здесь а=20, σ=5, α=10, β=25, δ=4.
Решение. Вероятность того, что нормальная случайная величина Х прим
 2015-04-17
2015-04-17 1886
1886