Уровень 3.
ЗАДАЧА №5.61.
Во всех этих заданиях видно, что
1) x стоит в точно такой же форме, что и x^2 (скажем в примере г -
(x+3)^2 и |x+3|)
2) Квадрат -x и квадрат x одинаковы, значит квадрат можно
заменить на квадрат модуля - ничего не изменится
3) Затем можно модуль заменить на новую переменную и получить
квадратное уравнение
а)
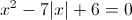
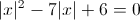
Пусть y=|x|
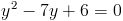
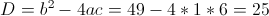
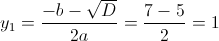
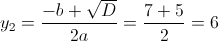
1) 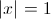
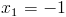
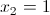
2) 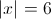
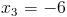
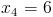
б)
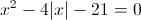
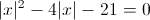
Пусть y=|x|
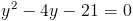
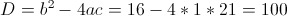
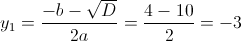
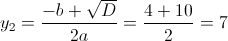
1) 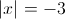
Такого не может быть, корней нет
2) 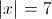
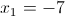
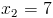
в)
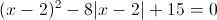
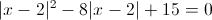
Пусть y=|x-2|
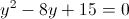
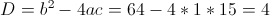
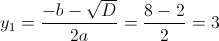
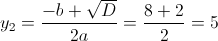
1) 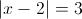
1-1) 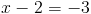
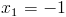
1-2) 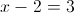
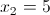
2) 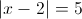
2-1) 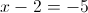
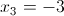
2-2) 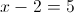
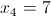
г)
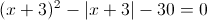
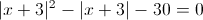
Пусть y=|x+3|
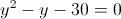
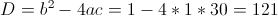
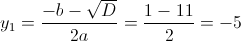
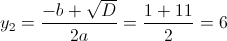
1) 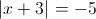
Такого не может быть, корней нет
2) 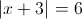
2-1) 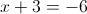
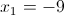
2-2) 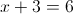
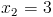
ЗАДАЧА №5.62.
а)
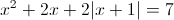
1) x>=-1
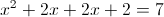
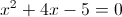
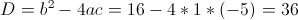
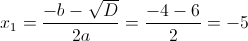
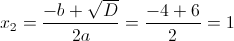
Нам подходит второй корень, так как он больше -1
2) x<-1
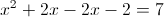
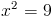
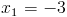
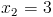
Нам подходит первый корень, так как он меньше -1
Итого решениями нашего уравнения являются x=1 и x=-3
б)
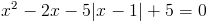
1) x>=1
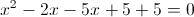
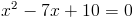
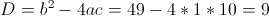
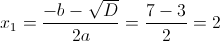
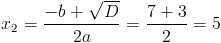
Оба этих числа больше одного, так что они нам подходят
2) x<1
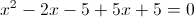
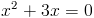
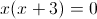
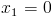
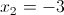
Оба этих числа меньше одного, так что они нам подходят
Итого решениями нашего уравнения являются x=-3, x=0, x=2, x=5
в)
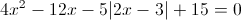
1) x>=3/2
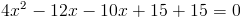
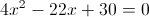
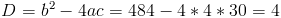
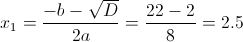
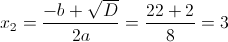
Оба этих числа больше 3/2, так что они нам подходят
2) x<3/2
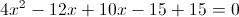
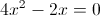
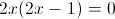
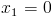
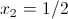
Оба этих числа меньше 3/2, так что они нам подходят
Итого решениями нашего уравнения являются x=0, x=1/2, x=5/2, x=3
г)
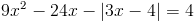
1) x>=4/3
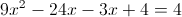
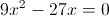
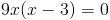
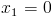
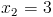
Нам подходит второй корень, так как он больше 4/3
2) x<4/3
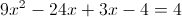
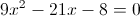
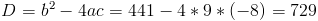
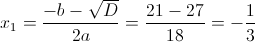
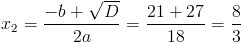
Нам подходит первый корень, так как он меньше 4/3
Итого решениями нашего у
равнения являются x=-1/3, x=3
5.63.
а)
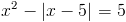
1) x>=5
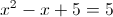
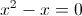
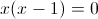
Откуда вытекает что x=0 или x=1, но эти числа меньше 5,
так что эти корни не походят
2) x<5
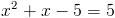
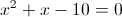
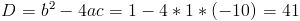
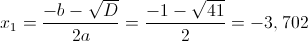
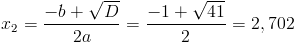
Оба этих числа меньше 5, и таким образом являются корнями
данного уравнения
б)
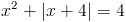
1) x<-4
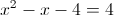
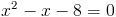
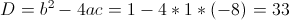
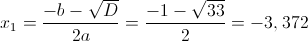
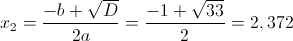
Оба этих числа больше чем -4, значит это не корни
2) x>=-4
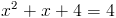
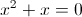
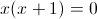
Откуда x=0 или x=-1. Оба этих числа больше -4, и таким образом
являются корнями данного уравнения
в) 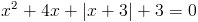
1) x<-3
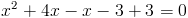
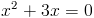
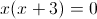
Откуда x=0 и x=-3. Оба этих числа "не меньше" -3. Следовательно
это не корни данного уравнения (в данном случае)
2) x>=-3
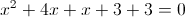
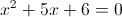
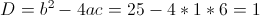
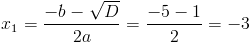
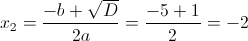
Оба этих числа больше или равны -3. Следовательно x=-3 и x=-2 являются
корнями данного уравнения.
г) 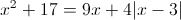
1) x>=3
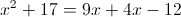
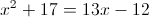
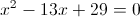
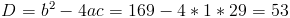
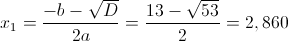
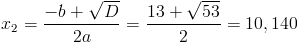
Из данных чисел только число 10,140>=3, следовательно оно является
корнем данного уравнения
2) x<3
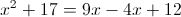
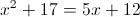
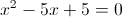
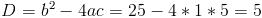
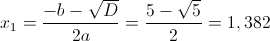
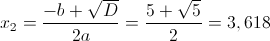
Из этих чисел только число 1,382 меньше трех, следовательно оно
является корнем данного уравнения.
Всего корней у уравнения два - 1,382 и 10,140
5.64.
а)
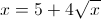
Пусть y=корень из x
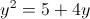
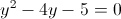
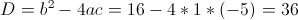
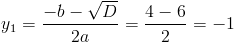
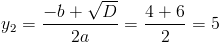
1) 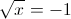
Корней нет, так как корень должен быть 0 или больше чем 0
2) 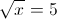
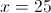
б)
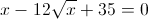
Пусть y=корень из x
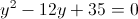
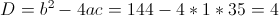
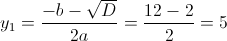
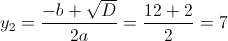
1) 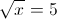
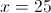
2) 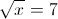
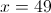
в)
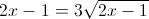
Пусть y=корень из 2x-1
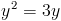
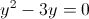
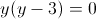
1) 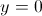
2) 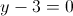
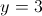
1) 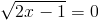
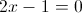
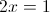
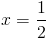
2) 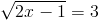
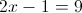
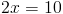
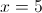
г)
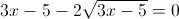
Пусть y=корень из 3x-5
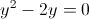
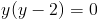
1) 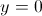
2) 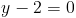
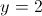
1) 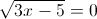
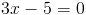
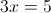
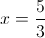
2) 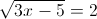
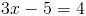
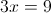
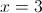
5.65.
а)
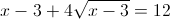
Пусть y=корень из x-3
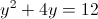
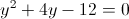
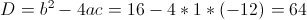
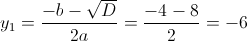
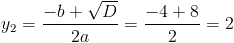
1) 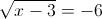
Корней в данном случае нет, так как корень должен быть больше
или равен нулю
2) 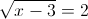
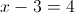
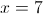
б)
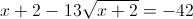
Пусть y=корень из x+2
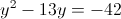
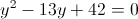
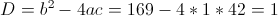
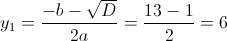
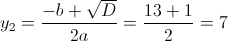
1) 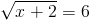
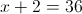
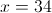
2) 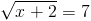
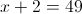
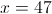
в)
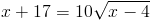
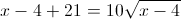
Пусть y=корень из x-4
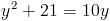
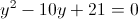
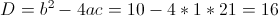
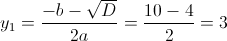
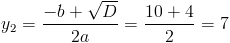
1) 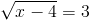
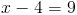
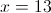
2) 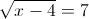
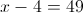
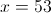
г)
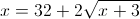
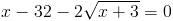
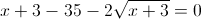
Пусть y=корень из x+3
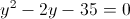
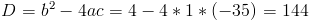
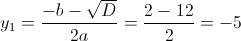
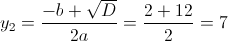
1) 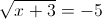
Корней в данном случае нет, так как корень должен быть больше
или равен нулю
2) 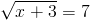
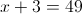
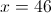
5.66.
а)
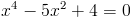
Пусть y=x^2
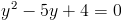
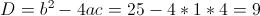
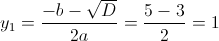
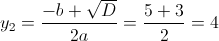
1) 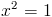
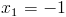
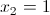
2) 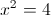
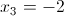
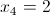
б)
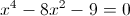
Пусть y=x^2
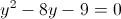
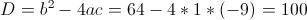
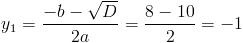
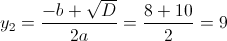
1) 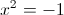
Корней нет, так как квадрат должен быть больше или равен нулю
2) 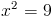
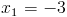
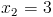
в)
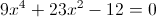
Пусть y=x^2
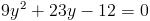
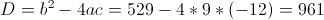
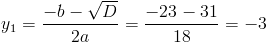
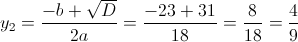
1) 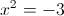
Корней нет, так как квадрат должен быть больше или равен нулю
2) 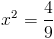
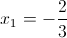
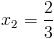
г)
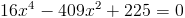
Пусть y=x^2
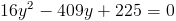
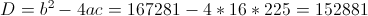
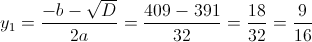
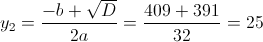
1) 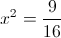
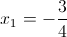
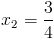
2) 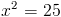
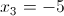
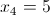
5.67.
а)
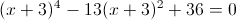
Пусть y=(x+3)^2
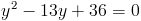
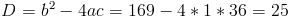
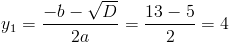
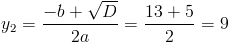
1)
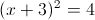
1a)
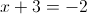
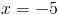
1б)
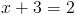
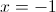
2)
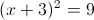
2a)
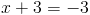
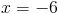
2б)
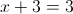
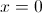
б)
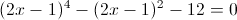
Пусть y=(2x-1)^2
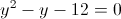
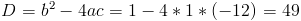
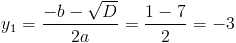
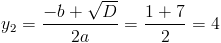
1)
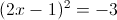
Корней нет
2)
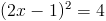
2a)
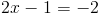
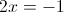
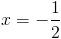
2б)
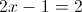
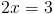
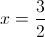
в)
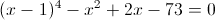
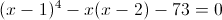
Пусть y=x-1
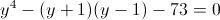
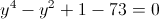
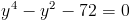
Пусть z=y^2
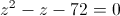
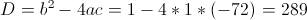
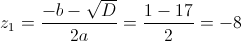
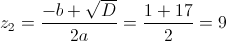
1)
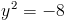
Корней нет
2)
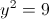
2a)
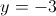
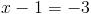
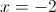
2б)
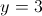
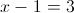
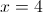
г)
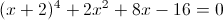
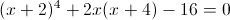
Пусть y=x+2
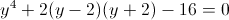
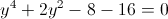
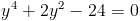
Пусть z=y^2
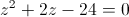
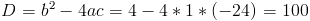
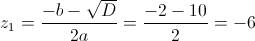
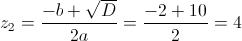
1)
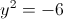
Корней нет
2)
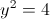
2a)
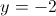
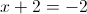
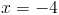
2б)
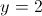
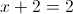
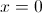
5.68.
а)
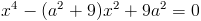
Пусть y=x^2
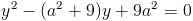
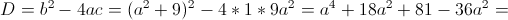
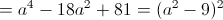
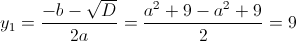
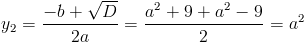
1)
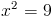
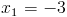
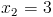
2)
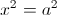
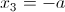
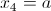
б)
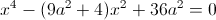
Пусть y=x^2
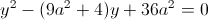
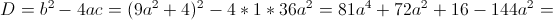
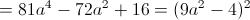
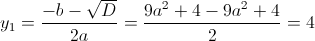
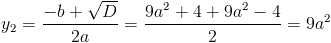
1)
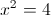
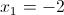
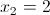
2)
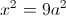
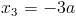
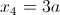
в)
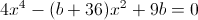
Пусть y=x^2
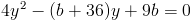
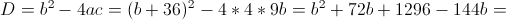
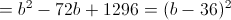
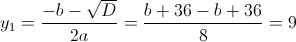
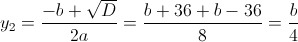
1)
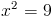
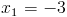
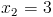
2)
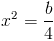
Тут заметим что b должно быть больше или равно нулю - так как
иначе квадрат будет отрицательным
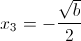
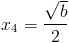
г)
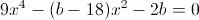
Пусть y=x^2
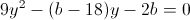
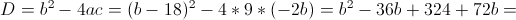
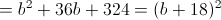
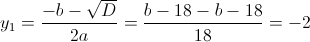
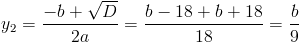
1)
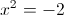
Корней нет, так как квадрат не может быть отрицателен
2)
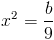
Тут заметим что b должно быть больше или равно нулю - так как
иначе квадрат будет отрицательным
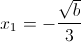
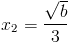
5.69.
а)
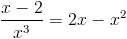
Прежде всего заметим, что при x=0 уравнение не имеет решения, так
как знаменатель обращается в ноль. Так что на x^3 можно домножить
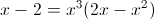
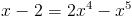
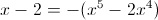
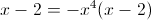
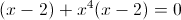
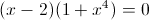
1) 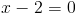
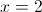
2) 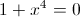
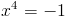
Корней нет, так как четвертая степень должна быть нулем
или положительным числом
б)
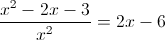
Прежде всего заметим, что при x=0 уравнение не имеет решения, так
как знаменатель обращается в ноль. Так что на x^2 можно домножить
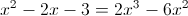
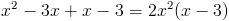
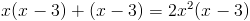
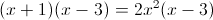
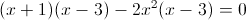
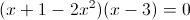
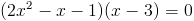
1) 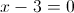
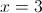
2) 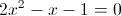
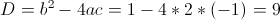
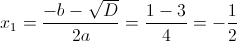
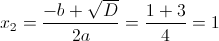
в)
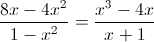
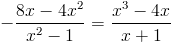
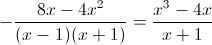
Заметим, что при x=-1 и x=1 знаменатель первой дроби обращается
в ноль - следовательно на (x-1)(x+1) можно домножить
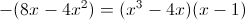
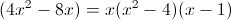
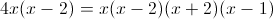
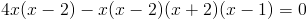
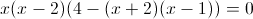
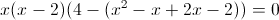
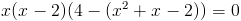
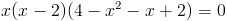
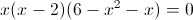
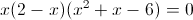
1) 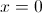
2) 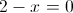
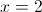
3) 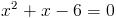
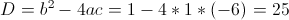
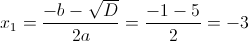
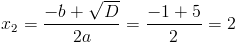
У нас получилось два корня x=2. На самом деле это конечно
один и тот же корень (просто двойной кратности)
г)
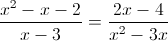
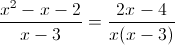
Заметим что при x=0 и x=3, знаменатель второй дроби обращается в
ноль, следовательно на x(x-3) можно домножить
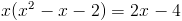
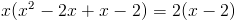
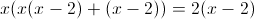
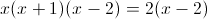
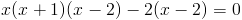
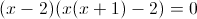
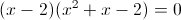
1) 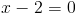
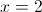
2) 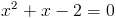
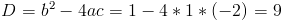
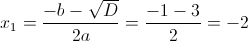
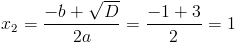
5.73.
а)
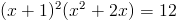
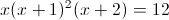
Пусть y=x+1
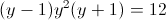
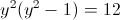
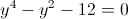
Пусть z=y^2
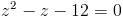
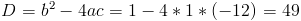
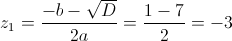
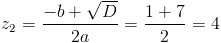
1) 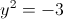
корней нет
2) 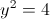
1а) 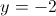
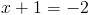
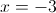
1б) 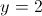
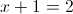
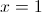
б)
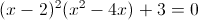
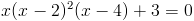
Пусть y=x-2
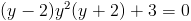
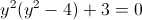
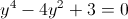
Пусть z=y^2
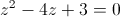
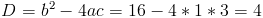
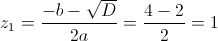
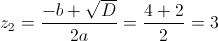
1) 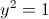
1а) 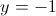
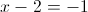
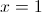
1б) 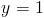
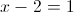
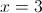
2) 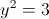
2а) 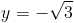

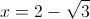
2б) 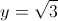
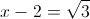
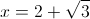
в) 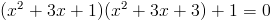
Пусть y=x^2+3x+2
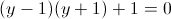
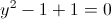
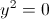
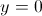
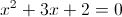
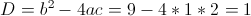
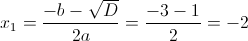
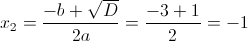
г) 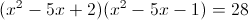
Пусть y=x^2-5x-1
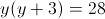
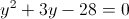
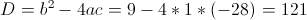
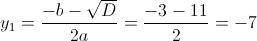
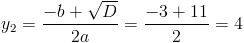
1) 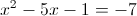
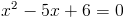
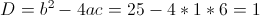
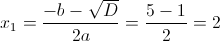
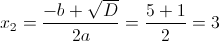
2) 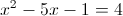
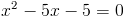
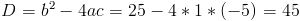
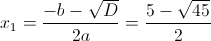
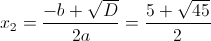
5.74.
а)
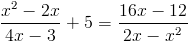
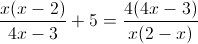
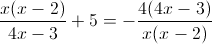
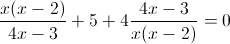
Пусть 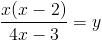
Тогда 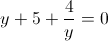
Умножим левую и правую часть на y (y не может быть равно нулю, так
как тогда знаменатель обращается в ноль)
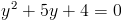
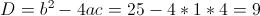
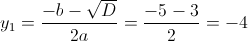
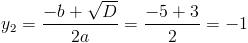
1) 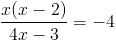
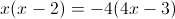
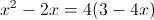
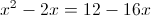
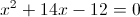
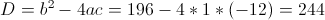
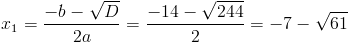
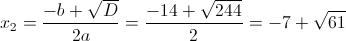
2) 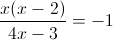
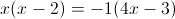
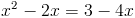
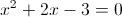
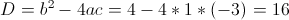
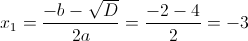
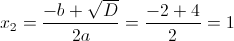
б)
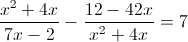
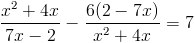
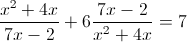
Пусть 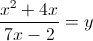
Тогда 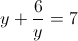
Умножим левую и правую часть на y (y не может быть равно нулю, так
как тогда знаменатель обращается в ноль)
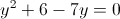
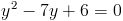
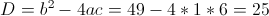
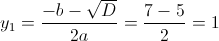
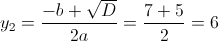
1) 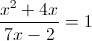
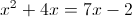
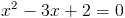
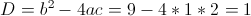
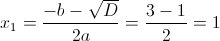
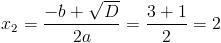
2) 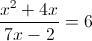
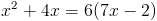
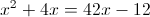
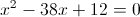
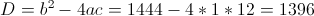
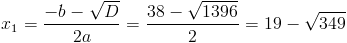
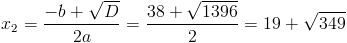
в) 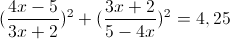
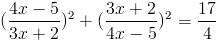
Пусть 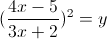
Тогда 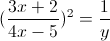
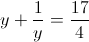
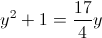
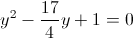
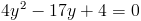
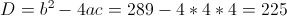
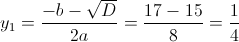
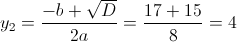
А) 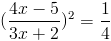
1) 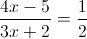
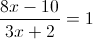
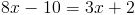
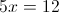
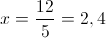
2) 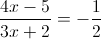
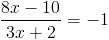
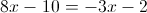
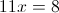
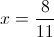
Б) 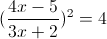
1) 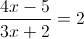
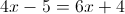
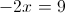
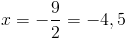
2) 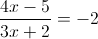
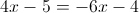
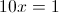
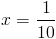
г) 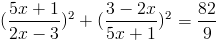
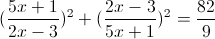
Пусть 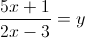
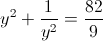
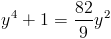
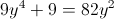
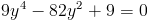
Пусть 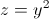
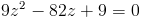
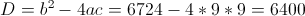
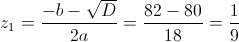
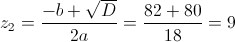
А) 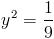
1) 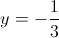
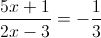
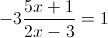
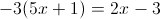
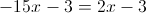
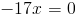
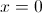
2) 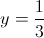
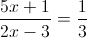
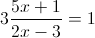
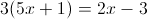
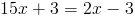
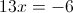
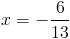
Б) 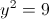
1) 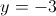
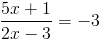
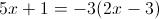
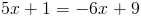
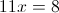
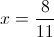
2) 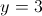
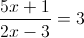
 2015-04-17
2015-04-17 229
229






