Фильтрация сигналов с помощью фильтра нижних частот (ФНЧ)

Предположим, что на входе идеального ФНЧ действует смесь сигнала 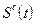со спектральной плотностью 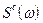и помехи 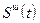со спектральной плотностью 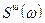и что сигнал и помеха статистически независимы. Обычно полезный сигнал менее широкополосен и его спектр падает с ростом. Очевидно, в этом случае существует некоторое оптимальное значение полосы пропускания фильтра - 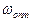, которое минимизирует среднеквадратическую погрешность фильтрации, поскольку увеличение полосы пропускания будет приводить к уменьшению погрешности 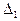от срезания высокочастотных составляющих спектра сигнала 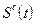, но будет увеличивать погрешность 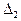от действия помехи 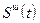Суммарное значение погрешности фильтрации, если пренебречь запаздыванием ФНЧ, можно записать в виде:

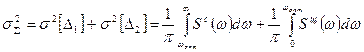
Оптимальное значение 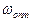можно найти из соотношения: .

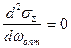Например, для телеграфного сигнала с экспоненциальной корреляционной функцией 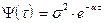, на который накладывается белый шум, оптможно найти следующим образом. Пусть 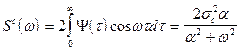, , 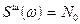так как

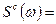
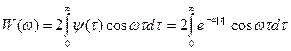
Учитывая что ; ;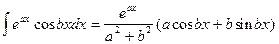

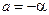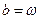
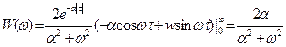,тогда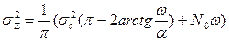

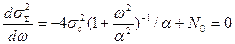
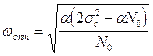
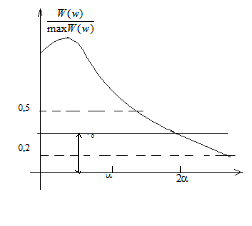Подбирая параметры фильтра (параметрическая оптимизация), можно добиться весьма эффективного сглаживания сигнала. Как уже было показано выше качество интерполяции с помощью хорошо настроенного ФНЧ выше, чем у интерполятора первого порядка.