Классическая формулировка. Если элемент можно выбрать k способами, а элемент можно выбрать m способами

Если элемент 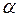можно выбрать k способами, а элемент 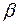можно выбрать m способами. Тогда 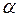или 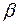можно выбрать k + m способами.

Современная формулировка (теорема о мощности объединения множеств)

Количество элементов объединения двух множеств равно сумме количества элементов в первом и во втором множестве, за вычетом количества элементов их пересечения:

.

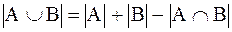Причем, если множества не пересекаются, то теорема приобретает вид, аналогичный классической формулировке:

.

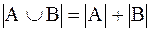Для трех множеств теорема имеет вид:

.

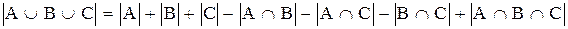Общее правило для 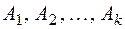имеет вид::

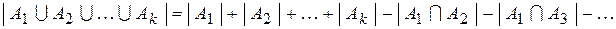
Пример. Староста одного курса дал следующие сведения о студентах: ”На курсе учатся 45 человек, в том числе 25 юношей. 30 человек учатся на хорошо и отлично, в том числе 16 юношей. Спортом занимаются 28 человек, в том числе 18 юношей и 17 человек, учащихся на хорошо и отлично. 15 юношей учатся на хорошо и отлично и занимаются спортом.” Проверьте правильность приведенных старостой сведений.

Для проверки правильности (непротиворечивости) приведенных данных используем теорию множеств и введем следующие обозначения.

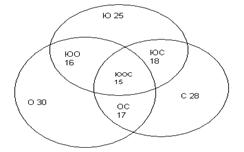Кроме того, для наглядности, изобразим полученные данные на диаграмме Венна.

Множество юношей обозначим буквой Ю, и по данным старосты количество юношей .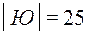

Множество спортсменов обозначим С и .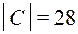

Множество отличников и хорошистов обозначим О и .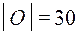

При этом из условия, что 30 человек учатся на отлично и хорошо, в том числе 16 юношей, имеем .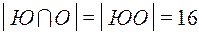

Из условия, что спортом занимаются 28 человек, в том числе 18 юношей и 17 человек, учащихся на отлично и хорошо, следует 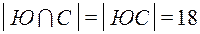и .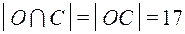

Из условия, что 15 юношей учатся на отлично и хорошо и занимаются спортом, следует .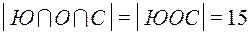

По правилу суммы, исходя из полученных от старосты данных, общее количество студентов курса, т.е. 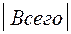, должно быть равно

.

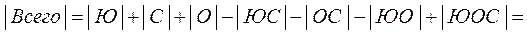
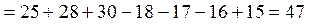Однако это противоречит исходному условию, что на курсе учатся всего 45 студентов.

Таким образом, в сведениях, поданных старостой курса, содержится ошибка.