2015-04-01
623
Результаты равноточных измерений получаются при многократных измерениях одного и того же истинного значения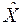 
измеряемой физической величины (ФВ), одним и тем же средством измерения, одним наблюдателем, при неизменных условиях измерения. Результат измерения при этом равен
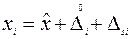, (1.1)
где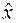 
- истинное значение;
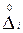и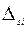 
- соответственно случайная и систематическая составляющие i - го результата.
Обычно величина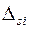 
известная и в результат измерения вносится поправка
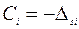, (1.2)
т.е. получается исправленный результат
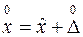. (1.3)
Задача обработки результатов найти оценку (приближенная характеристика) истинного значения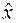
= 
. 
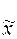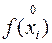(1.4)
Для оценки результата измерений, являющегося случайной величиной находят его характеристики: оценку математического ожидания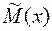 
- среднее значение, вокруг которого группируются все результаты и оценку среднего квадратического отклонения (с. к. о.) 
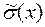, которая является мерой рассеяния результатов относительно центра группирования.
А Точечная оценка
При обработке результатов измерений необходимо воспользоваться свойствами математического ожидания и дисперсии.
|
|
|
Оценка называется точечной, если ее значения можно представить на числовой оси геометрически в виде точки.
1 Исправленный ряд результатов ранжируется
.
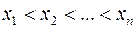2 Находится среднее арифметическое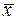 
(оценка математического ожидания 
)
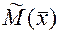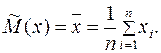
(1.5)
3 Проверяется правильность вычислений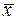
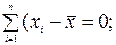(1.6)
.
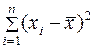4 Определяется оценка среднего квадратического отклонения (с. к. о.)
а) Оценка с. к. о. отдельного результата наблюдения (формула Бесселя)
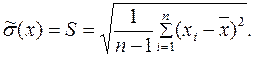(1.7)
Полученные точечные оценки по формулам (1.5) и (1.7) являются случайными, т.к. при повторных измерениях получим другую группу результатов, а для нее другие значения 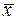и 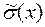. Поэтому для оценки полученного результата измерения величины 
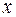необходимо оценить с. к. о. среднего арифметического 
.
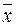б) Оценка с. к. о. среднего арифметического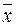
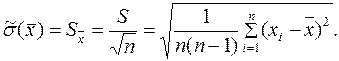(1.8)
В полученной группе результатов измерений один или два наблюдения (обычно это крайние результаты в ряде) могут резко отличаться от остальных. Поэтому их следует проверить на наличие в них грубых погрешностей с целью их исключения из ряда измерений, т.к. они могут сильно искажать 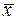, , 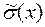закон распределения и доверительный интервал.
