Курсовая работа. Министерство образования и науки Российской Федерации

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

«Саратовский государственный технический университет имени Гагарина Ю.А.»

Кафедра «Радиоэлектроника и телекоммуникации»

Курсовая работа

по дисциплине «Численные методы»

на тему: « ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ »

Выполнил(а):

Факультет ИнЭТМ

Курс 1 (первый)

специальность сокращенная

заочная УПТС

Ф.И.О. ______________

________________________

Проверил(а):

к.э.н., доцент

Ушакова Ольга Валерьевна

Саратов – 2015

Цель работы: приобретение навыков построения интерполяционных полиномов по формулам Лагранжа и Ньютона для различных типов интерполируемых функций, алгоритмизация процесса интерполирования и оценки погрешности, исследование сходимости интерполяционного процесса.

Задание:

1. Вычислить коэффициенты 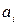(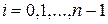) интерполяционного полинома 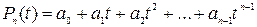, составленного для функции (1)

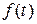(см. табл.) по первым трем узлам интерполирования двумя способами:

а) по формуле Лагранжа:

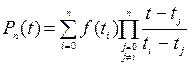, (2)

где 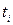(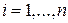) – узлы интерполирования, 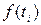(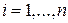) – значения заданной функции в узлах;

б) по формуле Ньютона:

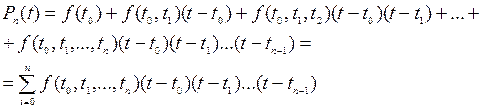(3)

где 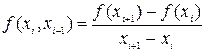- разделенные разности 1 порядка;

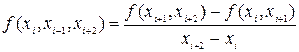- разделенные разности 2 порядка;

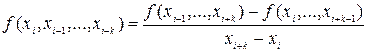- разделенные разности порядка .

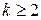Убедиться в том, что формулы (2) и (3) являются разными формами записи одного и того же интерполяционного полинома (1).

в) с помощью функции polyfit в среде MATLAB Version 7.5 (R2007b).

2. Составить блок-схему алгоритма и программу для вычисления значений двух заданных функци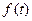й и ;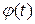

а) по исходной формуле;

б) по формуле Лагранжа или Ньютона

для двух значений узлов 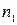и 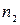с заданным шагом расчета. Оценить погрешность по формул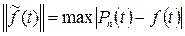е , где .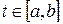

Программные средства, используемые для написания программы вычислений: Visual C++ 2005 Express Edition.

3. Произвести вычисления по программе. Результаты работы должны быть представлены в виде таблицы.

4. Оценить погрешность интерполирования в заданной точке 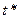по формуле

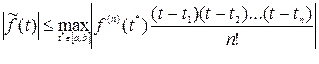. (4)