Двойственность в линейном программировании

Пусть некоторое предприятие имеет остатки k видов сырья, запасы которых 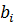. Из этого сырья можно изготовить п видов изделий. для которых известны технологические коэффициенты а_ij- и стоимость при реализации с_j. Некий заказчик предлагает купить на предприятии это сырье, но в его интересах сделать расходы минимальными. Предприятие же должно получить максимальную прибыль от продажи сырья, не меньшую, чем оно смогло бы получить при организации собственного производства.

Построим две математические модели для этой ситуации, выражающие интересы предприятия и заказчика.

Пусть x_j - количество единиц j-го вида продукции, тогда

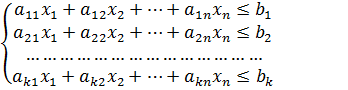(первая модель)

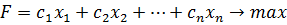
Пусть у_i - стоимость единицы i-го вида ресурса, тогда предприятие сможет отказаться от организации производства по выпуску продукции, если будут выполняться неравенства системы ограничений:

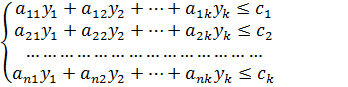(вторая модель)

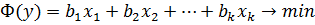
Величина у_i - это двойственные оценки или объективно обусловленные оценки, или теневые цены.

Обе указанные модели называются парой симметричных взаимно двойственных задач.

Особенности пары двойственных задач:

1. Любая из этих задач называется основной, а вторая - двойственной к ней.

2. Если в основной задаче целевая функция максимизируется, то в двойственной к ней - минимизируется, и наоборот.

3. Если в основной задаче все неравенства имеют знак 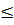, то в двойственной к ней - знак 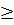, и наоборот.

4. Если в основной задаче коэффициенты b_i, входят в систему ограничений, а с_j- влинейную формулу, то в двойственной к ней задаче - наоборот.

5. Матрица коэффициентов системы ограничений в основной задаче имеет вид

а в двойственной к ней задаче эта матрица транспонирована:

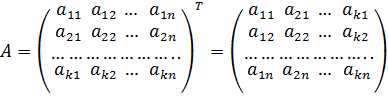
Двойственная задача - это тесно связанная пара задач. Из решения одной задачи по определенным правилам следует решение другой.

Замечание 1. Если в системе ограничений основной задачи имеются неравенства противоположных смыслов, то все неравенства приводятся к неравенствам одного смысла.

Замечание 2. Если целевая функция максимизируется, все неравенства должны иметь знак 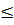, и наоборот, если целевая функция минимизируется, то все неравенства должны иметь знак 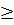. Если в системе ограничений встречаются неравенства противоположного смысла, то их нужно умножить на (-1).

Замечание 3. Если в системе ограничений имеется уравнение

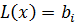то оно легко превращается в два неравенства противоположного смысла, т.е. в систему:

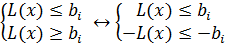
Пример. Дана задача. Пусть х_j - количество единиц продукции j -го вида.

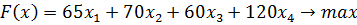
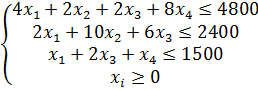
Составим двойственную задачу.

Пусть у_i - стоимость единицы i-го вида ресурса. Тогда покупатель должен заплатить согласно формуле

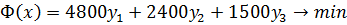
при условии, что он должен заплатить за единицу каждого вида теоретически произведенной продукции:

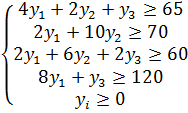
Двойственная пара задач составлена.

Основные теоремы двойственности

Теорема 1. Для любых допустимых планов двойственной задачи справедливо неравенство F(x) 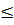Ф(у).

Теорема 2 (критерий оптимальности Канторовича).

Если для некоторых допустимых планов X, Y двойственной задачи выполняется равенство F(х) = Ф(у), то эти планы являются оптимальными для своих задач.

Теорема 3. Для существования оптимального плана двойственной пары задач необходимо и достаточно существование допустимого решения для каждой задачи из пары.

Теорема 4. Если одна из пары двойственных задач имеет оптимальное решение, то и другая задача тоже имеет оптимальное решение. Причем F(Х’) = Ф (Y’). Если же в одной из задач целевая функция неограниченно возрастает или убывает, то система ограничений в парной задаче противоречива.

Кол-во производимой продукции	Остатки ресурсов
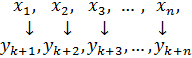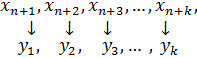Плата за ресурсы, потраченные на теоретически произведенную продукцию	Плата за остатки ресурсов

Сравнивая симплекс-таблицы для каждой из пары двойственных задач, можно отметить, что коэффициенты в индексной строке основной задачи являются значениями базисных переменных в парной к ней задаче, но только с противоположными знаками.

Если оптимальное решение существует, то в окончательном виде симплекс-таблицы в основной своей части будут иметь транспонированные матрицы, а числа в графах «План» и «Индексная строка» будут одинаковы по абсолютной величине с точностью до 90°, т.е. план основной задачи - индексная строка парной, индексная строка основной задачи - план двойственной.

Практический вывод.

Для решения двойственной задачи достаточно решить одну из задач и по соответствию переменных x₁, x₂, …, x_n. Найти решение второй задачи. Оптимальные значения целевых функций будут совпадать.

Пример. Пусть решая задачу мы получили следующую симплекс-таблицу:

Б	Ц	П	x1	x2	x3	x4	x5	x6	x7
x4			5/12	-1/6			1/2	-1/24
x3			1/3	5/3				1/6
x7			-1/12	-19/6			-1/8	-7/24
F		-5	-10			-15	-5

Составим схему соответствия переменных основной и двойственной к ней задач:

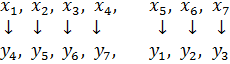
По индексной строке симплекс – таблицы определяем, что

,

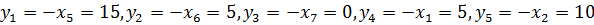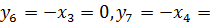0.

То есть оптимальное решение двойственной задачи имеет вид Y’ = (15; 5; 0; 5; 10; 0; 0) и оптимальное значение целевой функции

Ф(У’)=84000.

Значения у₁=15, у₂=5, у₃=0 представляют собой стоимостные оценки трудовых ресурсов, муки и работы электропечей. Это означает, что при оптимальном плане оценка ресурсов, затраченных на выпуск продукции, совпадает с оценкой произведенной продукции. Или, иначе, двойственные оценки гарантируют рентабельность оптимального плана.

Теорема 5 (об оценках).

Двойственные оценки у, показывают приращение функции цели 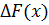, вызванное малым изменением свободных членов системы ограничений основной задачи.

Учитывая эту теорему, можно теперь определить, какие из ресурсов задачи являются более дефицитными. Итак, у* =(15; 5; 0; 5; 10;0;0):

Пусть b₁, (трудовые ресурсы) прирастет на единицу, тогда

.

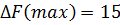Если b ₂ (мука) прирастет на единицу, тогда .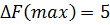

Если b₃ (время работы печей) прирастет на единицу, тогда

.

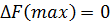Стоимостная оценка работы электропечей у₃ = 0 показывает, что этот ресурс на предприятии в избытке. А положительные оценки у₁= 15 и у₂ = 5 говорят о дефицитности этих ресурсов, причем трудовые ресурсы оказываются в большем дефиците по сравнению с таким ресурсом, как мука. И в этой ситуации следует принять еще рабочих, чтобы увеличить выручку.

Таким образом, оптимальные двойственные задачи показывают:

1) какие виды продукции выгодно изготавливать предприятию;

2) какие виды ресурсов являются дефицитными.

Замечание. Рассмотренные нами двойственные задачи являются стандартными (идеальными). Если же в системе ограничений будут содержаться и неравенства разного смысла и уравнения, то экономический анализ становится более сложным и требует применения и разработки специальных, более сложных методов.