2015-04-08
3850
Метод, используемый для измерения коэффициента усиления рупорной антенны, основан на следующей модели. Предположим, имеются 2 идентичные антенны, разнесённые на расстояние 2 R, которое удовлетворяет условию дальней зоны (3.1). Пусть при этом направление максимального излучения антенн совпадает с осевой линией системы (рис. 3.5). Очевидно, систему можно
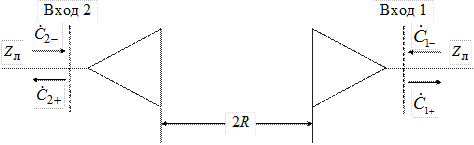
Рис. 3.5
рассматривать как волновой четырёхполюсник, который описывается матрицей рассеяния, причём ввиду симметрии системы между элементами матрицы имеются очевидные связи: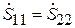 
, 
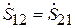. Следовательно, амплитуды падающих и расходящихся волн на входах 1 и 2 связаны соотношениями
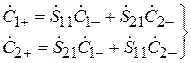. (3.9)
Элементы S -матрицы однозначно связаны с параметрами антенн и геометрией системы в целом. Для выяснения этих связей поставим систему в испытательный режим, при котором на вход 1 поступает падающая волна с комплексной амплитудой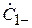 
, несущая мощность 
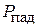, а вход 2 нагружен на согласованную нагрузку 
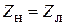(рис. 3.6). В этом случае 
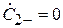и система (3.9) принимает вид
.
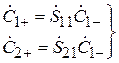Приведенные условия работы системы отображены на рис. 3.6.
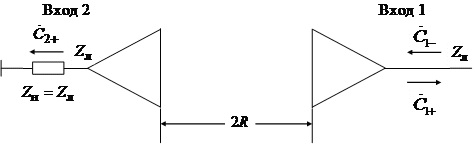
Рис. 3.6
Мощность, излучаемая первой антенной с учётом её КПД h,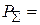 
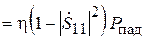, а плотность потока мощности, падающей на апертуру второй антенны:
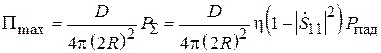. (3.10)
Антенна 2 в данном случае работает как приёмная и мощность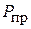 
, принимаемая ею, определяется выражением 
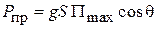, где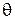 
– угол между нормалью к апертуре приёмной антенны и направлением на антенну передающую (в данном случае 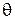= 0). В свою очередь, часть мощности 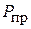переизлучается в окружающее пространство, а часть поступает в согласованную нагрузку. Мощность, поглощаемую в нагрузке приёмной антенны, можно рассчитать по формуле
,
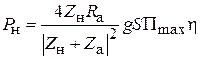где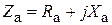 
– сопротивление излучения антенны.
Первый множитель в последнем равенстве равен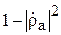 
, где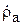 
– коэффициент отражения в линии с волновым сопротивлением 
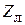, нагруженной на сопротивление 
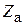. Учитывая (3.10), получим
.
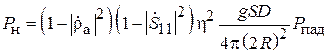Выражая далее gS через D и l из (3.2) и учитывая, что h D = G, найдём
.
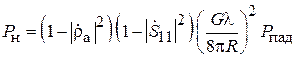Множитель перед 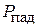представляет собой коэффициент прохождения мощности из линии 1 в линию 2, т. е. квадрат модуля элемента 
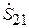, так что
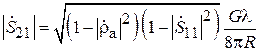. (3.11)
Фаза элемента 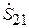зависит, очевидно, от электрического расстояния между антеннами и может быть представлена как 
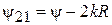, так что
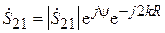. (3.12)
Перейдём к элементу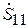 
S -матрицы рассматриваемой системы. Он имеет смысл коэффициента отражения на входе 1 в рассматриваемом испытательном режиме: 
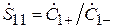. Но в линии 1 отражённая волна порождается двумя причинами: а) неидеальным согласованием антенны с линией, что в режиме излучения в свободное пространство было учтено коэффициентом отражения 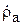, и б) вторичным излучением антенны 2, которое принимается антенной 1. В связи с этим в линии 1 появляется «добавочная» отражённая волна с амплитудой 
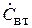. Таким образом, 
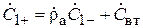, откуда 
.
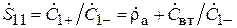Можно показать, что, поскольку антенны расположены на расстоянии, соответствующем дальней зоне, второе слагаемое в этом выражении будет существенно меньше первого (на один–два порядка) и им вполне можно пренебречь. Поэтому можно считать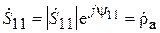 
. Теперь выражение (3.11) можно переписать в виде
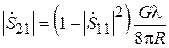, (3.13)
откуда
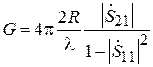. (3.14)
Таким образом, установлена связь между элементами S -матрицы и параметрами антенны.
Поставим теперь рассматриваемую систему в режим противофазного возбуждения, когда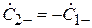 
. В этом случае, в соответствии с (3.9), 
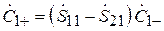, т. е. коэффициент отражения на входе 1 
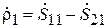, или, с учётом (3.12), (3.13),
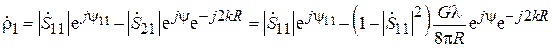. (3.15)
Следует отметить, что для реализации этого режима вовсе не обязательно иметь две идентичные антенны. Антенну 2, возбуждаемую в противофазе с антенной 1, можно заменить зеркальным изображением последней в идеально проводящем бесконечном экране, как показано на рис. 3.7.
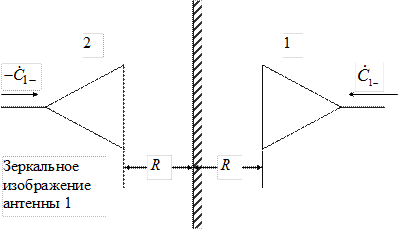
Рис. 3.7
Коэффициент усиления можно определить экспериментально, измеряя зависимость модуля коэффициента отражения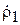 
в линии 1 от расстояния R до экрана. Действительно, при изменении R в выражении (3.15) первое слагаемое остаётся неизменным, а второе меняется по фазе (изменениями его модуля при небольших изменениях R можно пренебречь). В результате модуль коэффициента отражения 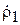будет изменяться, и по зависимости его от R можно найти значения 
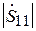и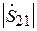 
, подстановка которых в (3.14) позволит найти значение КУ G.
В процессе выполнения эксперимента возможны 2 случая.
Случай 1: 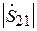< 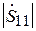. В данном случае векторная диаграмма, соответствующая формуле (3.15), показана на рис. 3.8, а. При изменении расстояния R вектор 
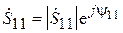неподвижен, а вектор 
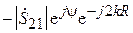вращается вокруг конца вектора 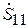. Максимальное по модулю значение 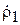получится при совпадении фаз этих векторов. Пусть это имеет место при некотором расстоянии 
:
, 
.
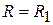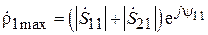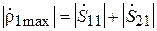При изменении R на l/4 (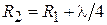
) фаза вектора 
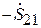изменится на p и модуль коэффициента отражения 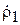станет минимальным (рис. 3.8, б). Фаза его будет при этом той же, что и при 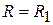, т. е. 
:
, 
.
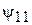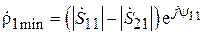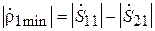При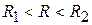 
значения 
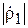будут промежуточными между 
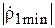и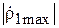 
.
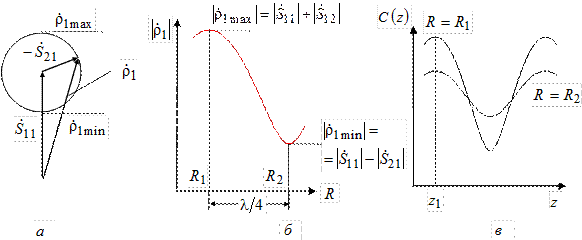
Рис. 3.8
Модули коэффициентов S -матрицы и 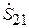будут, очевидно, определяться следующими выражениями:
, 
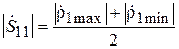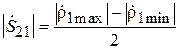. (3.16)
Обратим теперь внимание на следующий важный факт. При 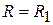во входной линии антенны создастся распределение поля C (z) с наименьшим значением КБВ, равным 
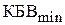(почему?). Пусть при этом максимум распределения поля расположен в некоторой точке с координатой 
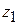(рис. 3.8, в). При переходе к 
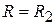во входной линии будет распределение поля с максимально возможным КБВ, равным 
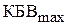(почему?). При этом максимум поля в линии будет находиться в той же точке 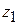, что и при 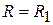. Это связано с тем, что коэффициент отражения в линии в обоих случаях имеет одну и ту же фазу 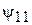на входе 1.
Случай 2: 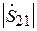> 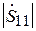. Векторная диаграмма для 
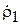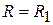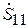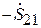в этом случае показана на рис. 3.9, а. При , как и в случае 1, при совпадении фаз векторов и коэффициент отражения 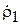максимален по модулю:
, .
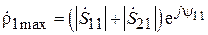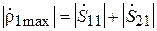Фаза вектора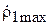 
равна при этом .
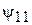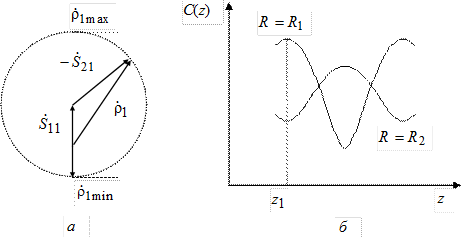
Рис. 3.9
При 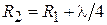фаза вектора 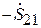изменяется на p. При этом вектор 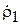становится минимальным по модулю и равным
.
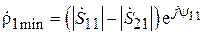Это выражение совпадает с аналогичным для случая 1. Однако, поскольку 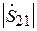> > 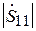, разность в скобках перед экспонентой отрицательна. Модуль коэффициента отражения в этом случае 
.
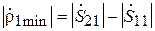Полный комплексный коэффициент отражения
.
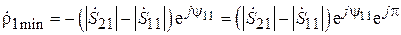Таким образом, при переходе от 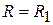к 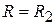коэффициент отражения в линии изменяется по фазе на p, чего не наблюдалось в случае 1. Поэтому, если при 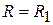в точке z = 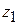находился максимум распределения поля, то при 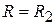в той же точке будет минимум (рис. 3.9, б).
Модули элементов S -матрицы 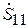и 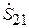определяться следующим образом:
, 
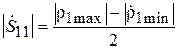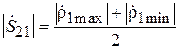. (3.17)
