Состояние равновесия характеризуется правилом фаз Гиббса, которое определяет связь между числом степеней свободы, числом ее компонентов и числом фаз.
Число независимых параметров, которые могут быть выбраны произвольно, чтобы привести систему в состояние равновесия – число степеней свободы.
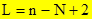 где L – число степеней свободы n – число компонентов N – число фаз
где L – число степеней свободы n – число компонентов N – число фаз
В качестве степеней свободы могут выступать t,P,c
Для 2-х компонентной системы взаимно растворимых жидкостей L=2, а для нерастворимых L=1
Вывод уравнения:
1) Пусть система содержит N фаз и n компонентов в каждой фазе.
2) Состояние фаз фиксировано при Р и Т.
3) Состав каждой фазы можно рассчитать, задавая n-1 концентраций компонентов, а концентрация одного из компонентов является зависимой величиной и может быть рассчитана из условия, что сумма мольных долей всех компонентов в смеси равна 1. 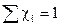
4) 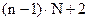 - общее число переменных, определяющих состояние системы.
- общее число переменных, определяющих состояние системы.
5) 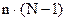 - общее число уравнений для расчета состояния системы, где (N-1) – число уравнений,
- общее число уравнений для расчета состояния системы, где (N-1) – число уравнений,
достаточных для расчета концентрации компонентов, n – число переменных.
6) Число уравнений не может превышать числа переменных, иначе уравнения будут несовместимыми. Разность между числом независимых переменных и числом уравнений равна числу произвольно изменяемых параметров в данной системе, меняя которые можно не менять число фаз в ней (степень свободы):
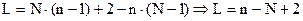
 2015-05-05
2015-05-05 394
394








