Достижимость

Говорят, что диграф обладает свойством достижимости, если между любыми вершинами диграфа существует хотя бы один путь.

Матрица достижимости R(u,v) задается следующим образом:

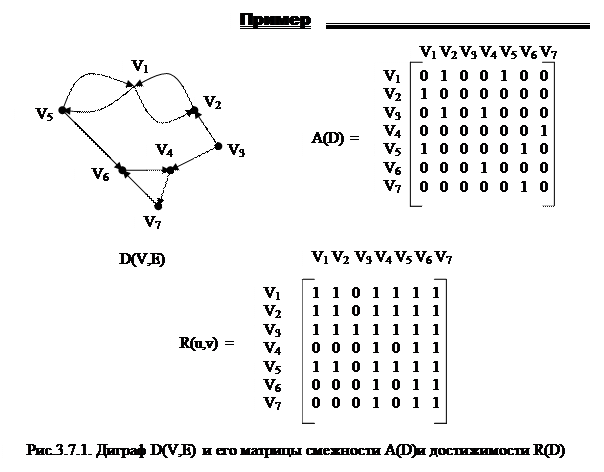Решение проблемы достижимости диграфа требует полиномиального времени, т.е. относится к Р-классу.

Построить матрицу достижимости можно с помощью алгоритма BFS, выполнив его из каждой вершины диграфа D(V,E).

Сложность – О(n(n+m).

o Начало BFS – вершина 1.

o Исследуются все вершины {1,y} A. Из вершины 1 доступны вершины 2 и 4. Эти вершины заносятся в специальную запись

String={2,4}.

o Затем исследуются все вершины {2,y} A. Из вершины 2 доступны вершины 3 и 5, которые заносятся в специальную запись:

String= {2,3,4,5}.

o Исследуются все вершины {4,y} A. Из вершины 4 доступна только вершина 5. Т.к. такая вершина уже есть в специальном списке, то запись остается неизменной.

o Следующими вершинами будут {3,y} A. Из вершины 3 доступна вершина 6. Эта вершина заносится в специальный список:

String={2,3,4,5,6}.

o Рассматриваются вершины {5,y} A. Доступными будут вершины 2 и 6, которые есть в специальном списке.

o Следующие вершины будут {6,y} A. Доступная вершина – вершина 5, которая имеется в специальном списке.

o BFS из вершины 1 завершен. В результате выполнения BFS сформирована специальная запись

String={2,3,4,5,6},

которая показывает вершины, доступные из вершины 1.

o Данная запись позволяет записать первую строку матрицы достижимости:

(0 1 1 1 1 1).

o Если повторить BSF из всех оставшихся вершин диграфа, то результатом будет следующая матрица достижимости:

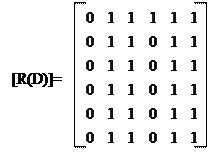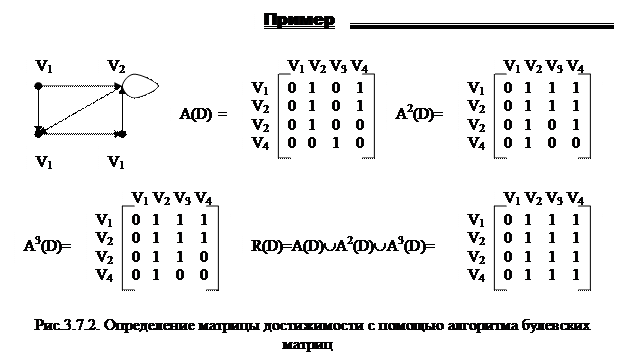
Матрицу смежности A(D) диграфа можно рассматривать как булевскую матрицу, т.к. элементы A(D) равны нулю или единице.

Матрица достижимости вычисляется следующим образом:

R(D) = A(D) Ú A²(D) Ú … Ú A^n-1, |V|=n,

где Ú - операция поэлементного булевского сложения строк матриц A(D),

A²(D), …, A^n-1;

Для облегчения вычисления степеней матриц A²(D), …, A^n-1 осуществляется с использованием булевских операций (умножение заменяется на Ù, а сложение – на Ú).

Сложность алгоритма – О(n⁴).

Правомочность использование булевских операций в данном алгоритме доказывается в целом ряде книг по диграфам.

Пусть [A(D)] – матрица смежности диграфа D=(V,E), n=|V|.

1. Пусть [Q₀]=[A(D)].

2. Сложить (булевская операция 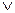) строку 1 матрицы [Q₀] к каждой строке [Q₀], которая имеет 1 в первом столбце. В результате получится матрица [Q₁]. Если первый столбец имеет только 0, тогда [Q₁]= [Q₀].

3. Сложить строку матрицы [Q₁] к каждой строке этой матрицы, которая имеет 1 во втором столбце. В результате получится матрица [Q₂]. Если втором столбце имеет только 0, тогда [Q₂]= [Q₃].

4. Для каждого j=3,…,n рассматривается матрица [Q_j-1]. Сложить строку j к каждой строке матрицы [Q_j-1], у которой j-ый столбец имеет 1. В результате получится матрица [Q_j]. Если j-ый столбец имеет только 0, тогда [Q_j]= [Q_j-1].

5. Записать [R(D)]=[Q_n].

Сложность алгоритма – O(n³).

· [Q₀]=[A(D)].

· Первая строка [Q₀] не имеет 1 в первом столбце. Поэтому [Q₁]=[Q₀].

· Строка 2 суммируется со строками 1 и 5 (имеют 1 во втором столбце):

· Строка 3 суммируется со строками 1,2 и 5:

· Сложить строку 4 со строкой 1. Результат – [Q₃]=[Q₄].

· Сложить строку 5 со строками 1,2,4,5 и 6:

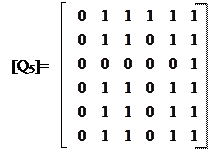· Сложить строку 6 со всеми строками:

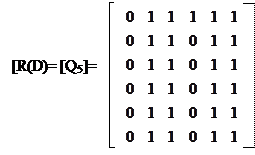3.8. Направленные деревья

Диграф D(V,E) называется направленным деревом, если он имеет корень r и если rÎ V и каждая вершина достижима из вершины r, т.е. имеются дипути, которые начинаются на r и заканчиваются на каждой вершине v.

Существуют несколько эквивалентных определений направленного дерева.

Пусть D = (V,E) будет диграфом. Тогда следующие определения эквивалентны:

· D является направленным деревом.

· D имеет корень, из которого имеется уникальный дипуть к каждой вершине.

· D имеет корень r, для которого deg⁺(r)=0, а для всех других вершин v deg⁺(v)=1.

· D имеет корень, но удаление дуги (но не вершины) нарушает это условие.

· Неограф основания диграфа D является связным и D имеет одну вершину r, для которой deg⁺(r)=0, а для остальных вершин v deg⁺(v)=1.

Вершины направленного дерева v, имеющие deg ^–(v)=0, являются его листьями. Направленный лес состоит из направленных деревьев.

Поддиграф H конечного диграфа D называется направленным каркасным деревом, если поддиграф Н является направленным деревом, содержащим все вершины D.

Число направленных каркасных деревьев с корнем r диграфа задается минором его матрицы Лапласа L⁺, который вычисляется при удалении r-ых строки и столбца.