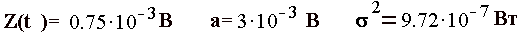Принятие решения по одному отсчёту

Сообщения передаются последовательностью двоичных символов «1» и «0», которые появляются с априорными вероятностями соответственно P(1)=0.09 и P(0)=0.91.

Этим символам соответствуют начальные сигналы S1 и S2,которые точно известны в месте приема. В канале связи на передаваемые сигналы воздействует Гауссовский шум с дисперсией D=0.972 мкВт. Приёмник, оптимальный по критерию идеального наблюдателя принимает решения по одному отсчету смеси сигнала и помехи на интервале сигнала длительностью Т.

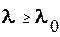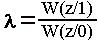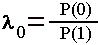Для принятия «1» по критерию идеального наблюдателя необходимо выполнение неравенства:

в противном случае принимается «0».

Для применения критерия идеального наблюдателя необходимо выполнение трех условий:

Чтобы сигналы были полностью известны.

1) Чтобы в канале связи действовали помехи с Гауссовским законом распределения.

2) Чтобы были известны априорные вероятности сигналов.

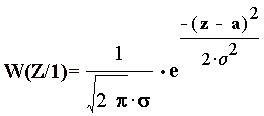Плотности вероятностей найдём по формулам:

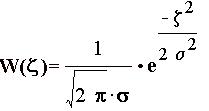Для вычисления плотности распределения помехи применим формулу:

Так как

(0.096<10.1), то на выходе решающего устройства будет зарегистрирован “0”.

Рассчитаем таблицы и построим графики для:

x		±s	±2s	±3s
W(x)				91.5

Z		-Z	+Z	-2Z	+2Z	-3Z	+3Z	+a
W(Z/0)
W(Z/1)		0.3		0.012		0.0003

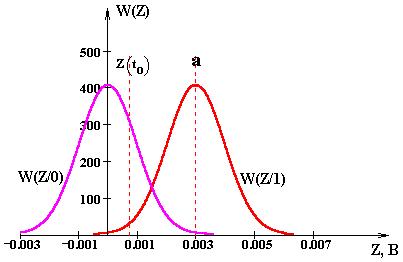
График плотностей распределения W(Z/1) и W(Z/0).

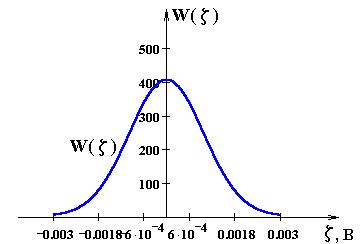
График плотности распределения помехи.