Уравнение Лагранжа II рода имеет вид:
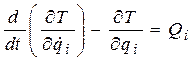 , i = 1,…, n. (57)
, i = 1,…, n. (57)
Здесь обозначено: T – кинетическая энергия системы; 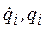 – соответственно обобщенная скорость и обобщенная координата. Скорость и координата называются обобщенными, поскольку могут быть как линейными, так и угловыми.
– соответственно обобщенная скорость и обобщенная координата. Скорость и координата называются обобщенными, поскольку могут быть как линейными, так и угловыми. 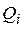 - обобщенная сила (может быть как силой, так и моментом); n – число степеней свободы системы. число степеней свободы системы с геометрическими связями (геометрическими называют связи, которые налагают ограничения на положение точек системы) равно числу независимых координат, с помощью которых можно однозначно определить положение системы. В общем случае точка системы может иметь бесконечное число возможных перемещений, но всегда найдется несколько возможных перемещений, через которые можно линейно выразить все остальные. Именно они и называются независимыми. Например, любое перемещение точки на плоскости можно выразить через два перемещения, соответствующие координатам x и y. Таким образом, точка на плоскости имеет две степени свободы. Вращающееся тело имеет одну степень свободы, так как его положение можно однозначно определить, задав всего одно перемещение – угол поворота. Обобщенную силу находят по формуле:
- обобщенная сила (может быть как силой, так и моментом); n – число степеней свободы системы. число степеней свободы системы с геометрическими связями (геометрическими называют связи, которые налагают ограничения на положение точек системы) равно числу независимых координат, с помощью которых можно однозначно определить положение системы. В общем случае точка системы может иметь бесконечное число возможных перемещений, но всегда найдется несколько возможных перемещений, через которые можно линейно выразить все остальные. Именно они и называются независимыми. Например, любое перемещение точки на плоскости можно выразить через два перемещения, соответствующие координатам x и y. Таким образом, точка на плоскости имеет две степени свободы. Вращающееся тело имеет одну степень свободы, так как его положение можно однозначно определить, задав всего одно перемещение – угол поворота. Обобщенную силу находят по формуле:
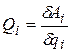 ,
,
где 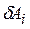 - работа сил, действующих на систему на возможном перемещении, при котором изменяется только обобщенная координата
- работа сил, действующих на систему на возможном перемещении, при котором изменяется только обобщенная координата 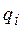 .
.
Например, для точки на рис. 28 обобщенные силы, соответствующие координатам x и y можно найти по формулам:
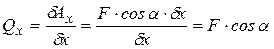 ,
,
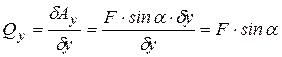 .
.
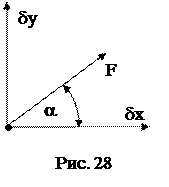
 2015-05-06
2015-05-06 823
823








