Теорема 1. Для подобных физических явлений существуют комплексы, составленные из величин, характеризующих эти явления, которые сохраняют одинаковое значение в сходственных точках подобных систем. Эти комплексы находят приведением дифференциальных уравнений к безразмерному виду.
Получают следующие комплексы:
1. Число Нуссельта:
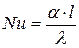
где l – характерный размер данной системы;
λ – коэффициент теплопроводности жидкости
Характеризует интенсивность теплообмена на границе среда - поверхность.
2. Число Прандтля:
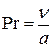
где 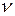 - коэффициент кинематической вязкости;
- коэффициент кинематической вязкости;
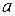 - коэффициент температуропроводности.
- коэффициент температуропроводности.
Pr - определяет физические свойства теплоносителя
3. Число Грасгофа:
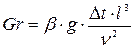
где 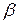 - объемного расширения (табличные данные).
- объемного расширения (табличные данные).
Для газов: 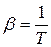
где 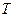 - термодинамическая температура газа для жидкости;
- термодинамическая температура газа для жидкости;
g - ускорение тяготения, 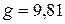 ,
, 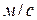 ;
;
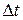 - температурный перепад,
- температурный перепад, 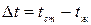 , С0
, С0
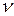 - коэффициент кинематической вязкости;
- коэффициент кинематической вязкости;
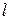 - геометрический размер, м.
- геометрический размер, м.
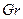 - зависимость между подъемной силой и силой вязкости. Характерезует свободную конвекцию.
- зависимость между подъемной силой и силой вязкости. Характерезует свободную конвекцию.
4. Число Рейнольдca:
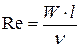
где – W - скорость потока жидкости или газа,
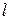 - геометрический размер для трубы
- геометрический размер для трубы 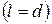
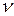 – коэффициент кинематической вязкоcти
– коэффициент кинематической вязкоcти
Re определяет зависимость между 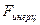 и
и 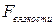 .
.
Теорема 2. Решение дифференциальных уравнений конвективного теплообмена может быть найдено как функция критериев подобия.
Gr, Pr, Re – определяющие критерии.
Nu – определяемый критерий.
Существует функция:
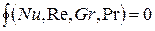
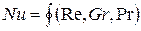 - критериальная зависимость для конвективного теплообмена.
- критериальная зависимость для конвективного теплообмена.
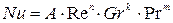 (13.2)
(13.2)
(13.2) – рабочее уравнение для нахождения коэффициента a, 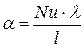
где 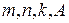 - находится в ходе эксперимента.
- находится в ходе эксперимента.
Определяющие параметры:
- температура: 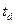 - температура стенки,
- температура стенки, 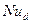 ;
;
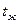 - температура потока жидкости,
- температура потока жидкости, 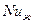
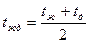 - средняя температура,
- средняя температура, 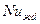
- геометрический размер: для трубы – диаметр 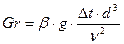
 2015-04-23
2015-04-23 226
226








