Замирание каналы часто моделируется как каналы Накагами с замираниями. Функция плотности вероятности (PDF) мгновенного SNR канала, γ над замиранием Накагами дается
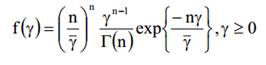 (4)
(4)
В (4), n управляет серьезность замирания, Γ (n) Гамма-функция определяется
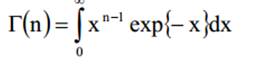
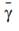 это среднее ОСШ канала. Если n = 1, PDF в (4) сводится к PDF γ над замиранием Рэлея дается:
это среднее ОСШ канала. Если n = 1, PDF в (4) сводится к PDF γ над замиранием Рэлея дается:
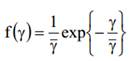
В качестве значения n растет, канал ведет себя как райсовского замирания, а при n выходит на ∞ канал сводится к каналу AWGN.
Пусть Рк вероятность выбора к-й режим из K схем возможных модуляции. Пусть ξ быть качество метрики канала. Таким образом, Pk может быть вычислена как функция ξ как
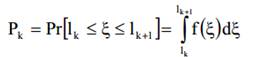 (5)
(5)
В (5), LK означает переключение режимов уровней и F (ξ) является PDF ξ. Средняя пропускная В в терминах среднего числа битов в секунду (бит), можно вычислить из
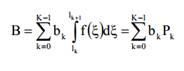
где b k является пропускной способностью отдельных мод. Когда l k = ∞, средняя
пропускная В может вычислена как
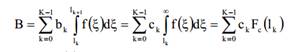
где 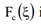 является комплементарной интегральной функции распределения (CDF) определяется
является комплементарной интегральной функции распределения (CDF) определяется
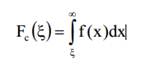
Если мгновенное значение ОСШ канала γ считается быть использованы в качестве канала
измерения ξ в нашей адаптивной схемы модуляции над Накагами замирание канала. Выбор режима вероятности Pk может быть вычислена из
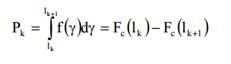
где дополняют CDF Fc (γ)определяется
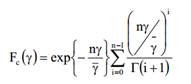
В канале с замиранием Рэлея, при n = 1, то вероятность выбора режима Pk дается
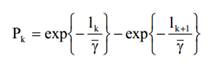
Средняя пропускная В от схемы адаптивной модуляции передачи по Накагами замирания канала задается
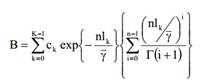
 2015-04-23
2015-04-23 1025
1025








