Далее вспомним методы дифференциального исчисления, используемые для исследования функций и построения их графиков.
Дифференциальное исчисление широко используется для исследования функций с целью построения их графиков.
Прежде чем перейти к рассмотрению первой задачи напомним некоторые моменты теории. Дадим определение локального максимума и минимума функции.
Точка 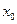 называется точкой локального максимума (минимума) функции
называется точкой локального максимума (минимума) функции 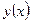 , если существует такая окрестность точки
, если существует такая окрестность точки 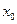 , что для всех точек
, что для всех точек 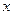 , принадлежащих этой окрестности, выполняется неравенство
, принадлежащих этой окрестности, выполняется неравенство 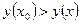 (
(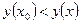 ).
).
Точки локального максимума и локального минимума называются точками экстремума функции.
Сформулируем теорему о необходимом условии существование экстремума.
Теорема. Точками экстремума непрерывной функции могут быть только такие точки, в которых ее производная или равна нулю или не существует.
Точки, в которых производная или равна нулю или не существует будем называть критическими точками.(Достаточные условия экстремума будут сформулированы несколько позднее.)
Задача 42. Найти наибольшее и наименьшее значение функции на заданном отрезке.
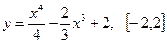 .
.
В этой задаче требуется найти наибольшее и наименьшее значения функции, заданной на некотором отрезке и непрерывной на этом отрезке. Из свойств непрерывной функции известно, что функция непрерывная на отрезке принимает на этом отрезке свое наибольшее и наименьшее значения. Если наибольшее или наименьшее значение достигается внутри отрезка, то эта точка является точкой экстремума, а значит критической точкой. Следовательно для определения наибольшего и наименьшего значений функции на некотором отрезке и непрерывной на этом отрезке может быть предложена следующая схема.
1. Находим производную функции.
2. Определяем критические точки (в которых производная или равна нулю или не существует) и выбираем те, которые лежат на данном отрезке.
3. Вычисляем значения функции в выбранных точках и на концах отрезка. Среди вычисленных значений выбираем наибольшее и наименьшее.
Решение.
Найдем критические точки функции, для чего вычислим производную функции и приравняем ее нулю:
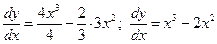
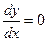 при
при 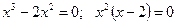 ,
,
откуда находим критические точки: 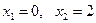 .
.
Далее необходимо выбрать те критические точки, которые принадлежат заданному отрезку. В данном случае обе критические точки ему принадлежат. Вычислим значения функции в критических точках и на концах отрезка и выберем наибольшее и наименьшее значения функции:
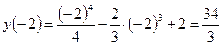 .
.
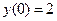 .
.
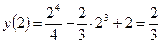 .
.
Делаем вывод о том, что свое наибольшее значение на заданном отрезке функция достигает при 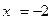 ,
, 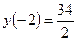 , а наименьшее значение при
, а наименьшее значение при 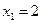 ,
, 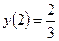 .
.
Задача 43. Найти наибольшее и наименьшее значение функции на заданном отрезке.
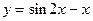 ,
, 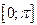 .
.
Находим производную: 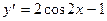 .
.
Находим критические точки: 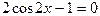 ;
; 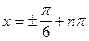 .
.
На отрезке 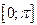 лежат
лежат 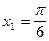 ,
, 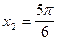 .
.
Вычисляем значения функции: 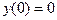 ;
; 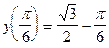 ;
; 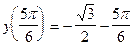 ;
; 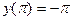 .
.
Наибольшее значение: 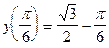 .
.
Наименьшее значение: 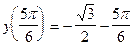 .
.
Общая схема следующих задач состоит в следующем. Требуется найти наибольшее или наименьшее значение некоторой величины (назовем ее S), зависящей от двух параметров (обозначим их 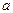 и
и  ) S(
) S(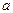 ,
,  ).
).
При этом параметры 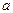 и
и  не являются не зависимыми, а связаны соотношением F(
не являются не зависимыми, а связаны соотношением F(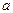 ,
,  )=0. Условия задачи позволяют определить возможную область изменения параметров. Это может быть отрезок или интервал.
)=0. Условия задачи позволяют определить возможную область изменения параметров. Это может быть отрезок или интервал.
Можно предложить следующий метод решения. Из соотношения F(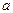 ,
,  )=0 один параметр может быть выражен через другой. Например,
)=0 один параметр может быть выражен через другой. Например,  =
=  (
(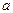 ). Тогда функция S становится функцией одного параметра
). Тогда функция S становится функцией одного параметра 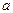 S=S(
S=S(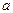 ,
,  (
(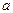 )). Если область возможного изменения параметра является отрезком, то дальнейшее решение в точности совпадает с решением предыдущей задачи. Если область изменения параметра является интервалом, то полезно воспользоваться следующим фактом.
)). Если область возможного изменения параметра является отрезком, то дальнейшее решение в точности совпадает с решением предыдущей задачи. Если область изменения параметра является интервалом, то полезно воспользоваться следующим фактом.
Если на некотором интервале функция имеет единственную точку экстремума и эта точка является точкой максимума (минимума), то значение функции в этой точке будет наибольшим (наименьшим) на всем интервале.
Сформулируем достаточные условия экстремума функции.
Если при переходе через критическую точку производная функции меняет знак с плюса на минус (с минуса на плюс), то эта точка является точкой максимума (минимума) функции. (Предполагается, конечно, что функция определена и непрерывна в данной точке.)
Задача 44. Прямоугольный участок огорожен с трех сторон забором периметра 4p. При каких размерах сторон площадь участка S будет наибольшей.
Решение. Обозначим 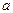 и
и  размеры сторон прямоугольника.
размеры сторон прямоугольника.
Тогда S= 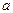
 . Параметры
. Параметры 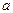 и
и  не являются независимыми, а связаны соотношением (длина забора)
не являются независимыми, а связаны соотношением (длина забора) 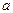 +2
+2  =4p. Тогда
=4p. Тогда 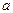 =4p-2
=4p-2  . Следовательно, функцию S можно представить как функцию одного параметра
. Следовательно, функцию S можно представить как функцию одного параметра  : S=
: S=  (4p-2
(4p-2  ).
).
Из условия задачи ясен, что параметр  может изменяться на следующем отрезке
может изменяться на следующем отрезке 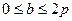 . То есть задача сводится к отысканию наибольшего значения функции S=S(
. То есть задача сводится к отысканию наибольшего значения функции S=S( )=
)=  (4p-2
(4p-2  ) на отрезке
) на отрезке 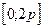 .
.
Найдем производную: 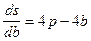 . Приравнивая ее нулю, получаем
. Приравнивая ее нулю, получаем  =p. Найденная точка лежит на отрезке
=p. Найденная точка лежит на отрезке 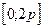 .
.
Вычисляем S(0)=0, S(2p)=0, 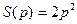 - это значение и является наибольшим. Тогда размеры сторон равны: a=2p, b=p.
- это значение и является наибольшим. Тогда размеры сторон равны: a=2p, b=p.
Задача 45. Объем цилиндрической цистерны равен V. При каких размерах площадь ее полной поверхности будет наименьшей.
Решение. Цилиндрическая цистерна характеризуется двумя параметрами: радиусом основания R и высотой H. Площадь полной поверхности выражается формулой S=2p 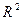 +2pRH. Параметры R и H не являются независимыми (известен объем), а связаны соотношением V=p
+2pRH. Параметры R и H не являются независимыми (известен объем), а связаны соотношением V=p 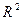 H. Тогда H=
H. Тогда H= 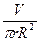 . Подставляя Н в выражение для площади полной поверхности, получим S как функцию одной переменной S(R)= 2p
. Подставляя Н в выражение для площади полной поверхности, получим S как функцию одной переменной S(R)= 2p 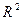 +
+ 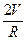 . Возможная область изменения параметра R интервал (0;¥).
. Возможная область изменения параметра R интервал (0;¥).
Найдем производную: 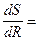 4pR-
4pR- 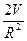 . Приравнивая ее нулю, получаем R=
. Приравнивая ее нулю, получаем R= 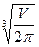 . Заметим что:
. Заметим что: 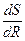 <0 при R<
<0 при R< 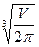 ,
, 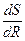 >0 при R>
>0 при R> 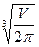 . Поскольку при переходе через данную критическую точку производная меняет знак с минуса на плюс, то эта точка является точкой минимума. Поскольку на интервале (0;¥) данная точка является единственной точкой экстремума, то значение функции в этой точке будет наименьшим. Получаем, что цистерна имеет наименьшую полную поверхность при R=
. Поскольку при переходе через данную критическую точку производная меняет знак с минуса на плюс, то эта точка является точкой минимума. Поскольку на интервале (0;¥) данная точка является единственной точкой экстремума, то значение функции в этой точке будет наименьшим. Получаем, что цистерна имеет наименьшую полную поверхность при R= 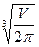 , H=
, H= 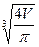 =2R.
=2R.
Задача 46. На странице книги печатный текст (вместе с промежутками между строками) должен занимать 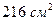 . Верхнее и нижнее поля должны быть по
. Верхнее и нижнее поля должны быть по 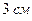 , правое и левое – по
, правое и левое – по 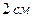 . Каковы должны быть размеры страницы для того, чтобы ее площадь была наименьшей?
. Каковы должны быть размеры страницы для того, чтобы ее площадь была наименьшей?
Решение. Исследуемая величина, для которой нам предлагается отыскать наименьшее значение, есть площадь печатной страницы. Обозначим ширину печатного текста через 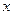 , а длину -- через
, а длину -- через 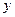 . Площадь всей страницы можно найти по формуле: S=(x+4)(y+6),
. Площадь всей страницы можно найти по формуле: S=(x+4)(y+6),
S=xy+6x+4y+24. Таким образом, мы выразили функцию, для которой необходимо найти наименьшее значение, как функцию двух переменных. Используем данную в условии задачи площадь печатного текста 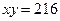 , тогда
, тогда 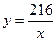 и выразим площадь страницы как функцию переменной
и выразим площадь страницы как функцию переменной 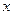 :
:
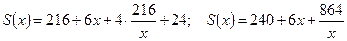 .
.
Из условия задачи вытекают естественные ограничения на значения переменной 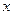 : 0<x<¥. Таким образом, мы решаем задачу о нахождении наименьшего значения функции на заданном интервале. Найдем критические точки функции, приравняв ее производную нулю.
: 0<x<¥. Таким образом, мы решаем задачу о нахождении наименьшего значения функции на заданном интервале. Найдем критические точки функции, приравняв ее производную нулю.
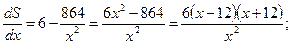
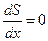 при
при 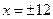 .
.
В соответствии с ограничениями, наложенными на 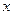 , рассматриваем критическую точку
, рассматриваем критическую точку 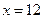 , принадлежащую заданному интервалу. Определим, с помощью достаточного условия экстремума, будет ли найденная точка точкой локального максимума функции. Для этого проверим знак производной в окрестности точки
, принадлежащую заданному интервалу. Определим, с помощью достаточного условия экстремума, будет ли найденная точка точкой локального максимума функции. Для этого проверим знак производной в окрестности точки 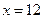 .
.
При x<12 имеем 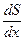 <0, при x>12 имеем
<0, при x>12 имеем 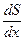 >0. Данная точка является точкой минимума. Поскольку эта точка является единственной критической точкой интервале, то значение в этой точке будет наименьшим.
>0. Данная точка является точкой минимума. Поскольку эта точка является единственной критической точкой интервале, то значение в этой точке будет наименьшим.



 Таким образом, площадь печатной страницы будет наименьшей, если ее длина равна
Таким образом, площадь печатной страницы будет наименьшей, если ее длина равна 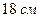 , а ширина
, а ширина 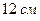 .
.
Далее рассмотрим полную схему исследования функции и построения ее графика. Основные требования мы приведем на примере решения конкретной задачи.
Задача 47. Методами дифференциального исчисления провести полное исследование функции и построить ее график: 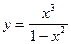 .
.
Эту задачу мы рассмотрим более подробно. Непосредственно в ходе решения мы будем приводить некоторые моменты теории. Схему построения графика мы покажем по шагам, предполагая, что в начале график строится на черновике, то есть схематично.
Полное исследование включает следующие моменты.
1. Область определения функции (ОДЗ).
Исследуемая функция 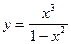 определена на всей числовой оси за исключением тех точек, где знаменатель обращается в ноль.
определена на всей числовой оси за исключением тех точек, где знаменатель обращается в ноль.
Найдем эти точки: 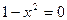 ;
; 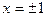 .
.
Следовательно, ОДЗ данной функции является вся числовая ось за исключением точек 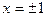 .
.
2. Четность, нечетность функции.
Напомним, что: функция называется четной, если y(-x)=y(x); функция называется нечетной, если y(-x)=-y(x). Напомним, что четная функция симметрична относительно оси Y, нечетная симметрична относительно начала координат. Если функция не является ни четной, ни нечетной, то говорят, что данная функция является функцией общего вида.
Для исследуемой функции имеем: 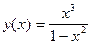 ;
;
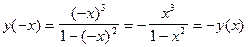 .
.
Следовательно, исследуемая функция является нечетной.
3. Нули, точки разрыва, точки пересечения графика с осями координат.
Для определения нулей функции решаем уравнение y(x)=0.
Имеем: 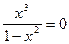 ; x=0. Следовательно, исследуемая функция обращается в ноль в единственной точке x=0.
; x=0. Следовательно, исследуемая функция обращается в ноль в единственной точке x=0.
Элементарная функция имеет точки разрыва только в тех точках, где она не определена. Следовательно, исследуемая функция имеет две точки разрыва 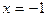 ,
, 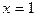 .
.
График функции пересекается с осью Х в тех точках, где она равна нулю. Эти точки уже найдены.
Определим точку пересечения с осью Y. Имеем y(0)=0.
Отметим, что в данной задаче точка пересечения с осью Х и точка пересечения с осью Y совпали, то есть график функции проходит через начало координат.
4. Интервалы знакопостоянства функции.
Для определения интервалов знакопостоянства функции напомним следующий факт.
Функция может изменить свой знак лишь при переходе через такие точки, в которых она равна нулю или имеет точку разрыва.
Исследуемая функция равна нулю при х=0. Имеет точки разрыва при х=-1 и х=1. Эти точки разбивают числовую ось на интервалы: (-¥;-1); (-1;0); (0;1); (1; ¥). На каждом из интервалов функция сохраняет постоянный знак. Чтобы определить знак функции на любом интервале, достаточно ее вычислить в любой точке интервала. Например, определим знак на интервале (0;1). Возьмем точку 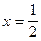 , лежащую на этом интервале. Вычислим
, лежащую на этом интервале. Вычислим 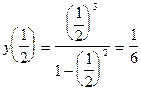 >0. Следовательно, исследуемая функция положительна на интервале (0;1). Аналогично исследуются знаки функции на остальных интервалах. Результаты удобно свести в таблицу.
>0. Следовательно, исследуемая функция положительна на интервале (0;1). Аналогично исследуются знаки функции на остальных интервалах. Результаты удобно свести в таблицу.
| x (интервал изменения) | (-¥;-1) | (-1;0) | (0;1) | (1; ¥) |
| у (знак функции) | + | - | + | - |
Напомним, что прямая х=а является вертикальной асимптотой графика функции у=у(х), если хотя бы один из пределов 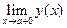 или
или 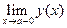 равен бесконечности. Вертикальные асимптоты могут быть только в точках разрыва функции.
равен бесконечности. Вертикальные асимптоты могут быть только в точках разрыва функции.
В исследуемой функции имеются две точки разрыва. При стремлении к этим точкам знаменатель дроби стремится к нулю, а числитель к ненулевой конечной величине. Следовательно, выражение будет стремиться к бесконечности. Знак бесконечности можно определить из таблицы интервалов знакопостоянства функции. Например, в окрестности точки х=-1 (x<-1) функция положительна. Следовательно
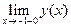 =
= 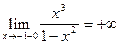 .
.
Аналогично:
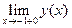 =
= 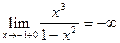 ;
;
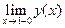 =
= 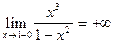 ;
;
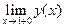 =
= 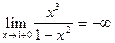 .
.
5б. Наклонные асимптоты.
Напомним, что прямая y=kx+b является наклонной асимптотой графика функции y=y(x) при x®+¥, если 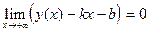 .
.
Достаточные условия существования асимптот и формулы для нахождения параметров k и b имеют вид.
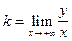 ;
; 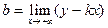 .
.
Если хотя бы один из этих пределов не существует или равен бесконечности, то функция не имеет асимптот при x®+¥. Аналогично определяется асимптота при x®-¥.
В исследуемой задаче асимптоты при x®-¥ и при x ®+¥ одинаковы. Поэтому мы будем рассматривать предел при x ®¥.
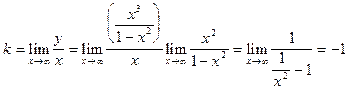 .
.
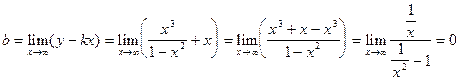 .
.
 |
Уравнение наклонной асимптоты имеет вид y=-x.
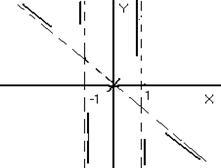
С этого момента на черновике можно начинать строить схему графика. Нанесем точки пересечения с осями координат, асимптоты и поведение функций около асимптот.
6. Интервалы возрастания, убывания функции. Точки экстремума.
Напомним достаточные условия возрастания (убывания) на отрезке.
Если производная функции положительна (отрицательна) во всех точках отрезка, то функция возрастает (убывает) на этом отрезке.
Необходимые и достаточные условия экстремума были сформулированы ранее.
6а. Найдем производную функции.
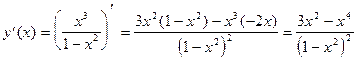 .
.
6б. Определим интервалы знакопостоянства производной. Интервалы возрастания и убывания функции.
Интервалы знакопостоянства производной определяются по той же схеме, что и ранее определялись интервалы знакопостоянства функции.
Производная имеет точки разрыва при х=-1, х=1.
Производная равна нулю: 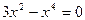 ;
; 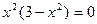 ; х=0,
; х=0, 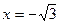 , x=
, x= 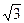 .
. 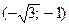
Точки х=-1, х=1, х=0, 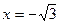 ,
, 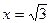 разбивают числовую ось на 6 интервалов. Как и ранее определяем знак производной на каждом интервале. На основании знака производной делаем вывод о характере поведения функции на интервале (возрастание или убывание). Результаты удобно свести в таблицу. В таблице
разбивают числовую ось на 6 интервалов. Как и ранее определяем знак производной на каждом интервале. На основании знака производной делаем вывод о характере поведения функции на интервале (возрастание или убывание). Результаты удобно свести в таблицу. В таблице

 знак указывает на возрастание функции, знак на убывание.
знак указывает на возрастание функции, знак на убывание.
| x | 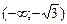 | 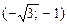 | (-1;0) | (0;1) | (1; 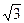 ) ) | (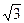 ;¥) ;¥) |
| y¢ | - | + | + | + | + | - |
      y y |
6в. Точки экстремума функции. Точками экстремума могут быть только те точки, в которых производная или равна нулю или не существует.
У исследуемой функции таких точек пять: х=-1, х=1, х=0, 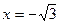 ,
, 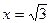 . В точках х=-1, х=1 функция не определена, а значит, они не могут быть точками экстремума.
. В точках х=-1, х=1 функция не определена, а значит, они не могут быть точками экстремума.
При переходе через точку х=0 знак производной не изменяется, а значит, она не является точкой экстремума.
При переходе через точку 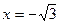 производная меняет свой знак с минуса на плюс и, следовательно, точка
производная меняет свой знак с минуса на плюс и, следовательно, точка 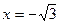 является точкой минимума. При переходе через точку
является точкой минимума. При переходе через точку 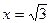 производная меняет свой знак с плюса на минус и, следовательно, точка
производная меняет свой знак с плюса на минус и, следовательно, точка 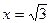 является точкой максимума.
является точкой максимума.
 |
Вычислим значения функции в точках экстремума:
точка 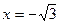 является точкой минимума,
является точкой минимума, 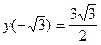 .
.
точка 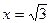 является точкой максимума,
является точкой максимума, 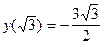 .
.
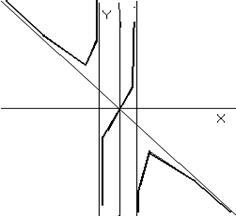
С учетом проведенного исследования уже может быть построен схематичный график.
7. Выпуклость, вогнутость, точки перегиба графика функции.
Напомним некоторые понятия. Функция называется выпуклой (вогнутой) на некотором отрезке, если ее график лежит ниже (выше) касательной, проведенной в любой точке этого отрезка.
Сформулируем достаточные условия. Если вторая производная функции отрицательна (положительна) на отрезке, то данная функция является выпуклой (вогнутой) на этом отрезке.
Точкой перегиба называется такая точка, в которой существует касательная, и в окрестности которой график функции лежит по разные стороны касательной.
Достаточные условия точки перегиба формулируются следующим образом. Если в некоторой точке определена первая производная и при переходе через эту точку вторая производная меняет свой знак, то такая точка является точкой перегиба.
7а. Находим вторую производную. 
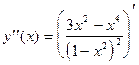 =
= 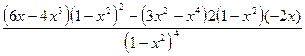 =
= 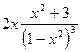 .
.
7б. Находим нули и точки разрыва второй производной, интервалы знакопостоянства второй производной. Определяем интервалы выпуклости и вогнутости функции.
Вторая производная равна нулю только в одной точке: х=0.
Вторая производная имеет точку разрыва в точках: х=-1, х=1.
Как и в предыдущем случае определяем интервалы знакопостоянства, и на основании знака второй производной делаем вывод о выпуклости или вогнутости функции. Результаты удобно свести в таблицу. В таблице выпуклость функции будем обозначать символическим знаком Ç, вогнутость знаком È.
| х | (-¥;-1) | (-1;0) | (0;1) | (1;+ ¥) |
| у¢¢ | + | - | + | - |
| у | È | Ç | È | Ç |
7в. Точки перегиба.
Вторая производная меняет знак в точках: х=-1; х=0; х=1.
Однако в точках х=-1 и х=1 функция не определена. Поэтому точкой перегиба является единственная точка х=0. Значение функции в этой точке у(0)=0.
С учетом исследования на выпуклость и вогнутость подправляем полученный ранее график плавной кривой. Таким образом, получаем окончательный вид графика функции.
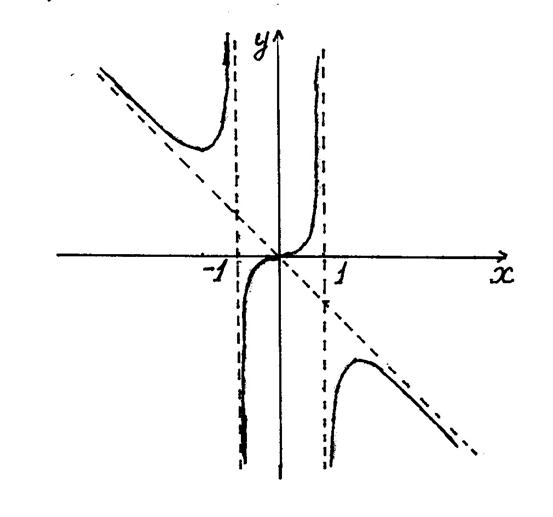
Задача 48. Методами дифференциального исчисления провести полное исследование функции и построить ее график: 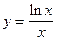 .
.
1.Область определения функции (ОДЗ).
Функция 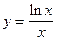 определена при x>0.
определена при x>0.
2. Четность, нечетность функции.
Поскольку функция не определена при x 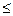 0, то данная функция является функцией общего вида.
0, то данная функция является функцией общего вида.
3. Нули, точки разрыва, точки пересечения графика с осями координат.
Нули функции. Решаем уравнение y(x)=0.
Имеем: 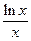 =0; x=1. Следовательно, исследуемая функция обращается в ноль в единственной точке x=1.
=0; x=1. Следовательно, исследуемая функция обращается в ноль в единственной точке x=1.
Данная функция непрерывна на всей области допустимых значений.
Точка пересечения с осью Х, точка х=1.
Поскольку функция не определена при х=0, то ее график не пересекается с осью Y.
4. Интервалы знакопостоянства функции.
В области допустимых значений знак функции может меняться в единственной точке х=1. Точка х=1 разбивает область допустимых значений на два интервала (0;1) и (1; ¥). Определяем значения функции на каждом интервале и результаты сводим в таблицу.
| x | (0;1) | (1;+¥) |
| y | - | + |
5а. Вертикальные асимптоты.
В области допустимых значений функция непрерывна. Поэтому асимптоты могут быть только на границе области допустимых значений.
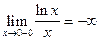 .
.
5б. Наклонные асимптоты.
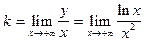 . Данный предел является пределом вида
. Данный предел является пределом вида 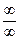 . Применяем правило Лопиталя.
. Применяем правило Лопиталя. 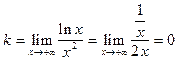 .Поскольку k=0, то:
.Поскольку k=0, то:
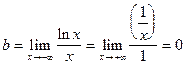 . (При вычислении предела использовано правило Лопиталя.)
. (При вычислении предела использовано правило Лопиталя.)
Таким образом уравнение асимптоты при 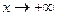 имеет вид
имеет вид
y=0.
6. Интервалы возрастания, убывания функции. Точки экстремума.
Находим производную:
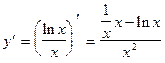 =
= 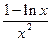 .
.
В области допустимых значений производная не имеет точек разрыва.
Нули производной находим, решая уравнение 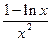 =0;
=0; 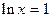 ;
; 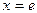 .
.
Точка 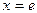 разбивает область допустимых значений на два интервала
разбивает область допустимых значений на два интервала 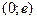 и
и 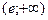 . Определяем знаки производной на каждом интервале и по знакам производной определяем интервалы возрастания и убывания функции. Результаты сводим в таблицу.
. Определяем знаки производной на каждом интервале и по знакам производной определяем интервалы возрастания и убывания функции. Результаты сводим в таблицу.
| x | (0; 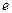 ) ) | (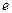 ;+¥) ;+¥) |
| y¢ | + | - |
  y y |
В точке 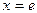 производная меняет знак с плюса на минус. Значит, точка
производная меняет знак с плюса на минус. Значит, точка 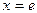 является точкой максимума функции. Вычислим значение функции в этой точке. Имеем
является точкой максимума функции. Вычислим значение функции в этой точке. Имеем 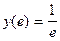 .
.
7. Выпуклость, вогнутость, точки перегиба графика функции.
Находим вторую производную
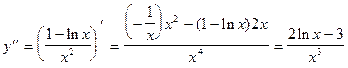 .
.
В области допустимых значений вторая производная точек разрыва не имеет. Для определения точек, в которых она равна нулю, решаем уравнение 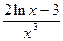 =0;
=0; 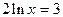 ;
; 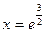 ;
; 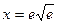 .
.
Определяем интервалы знакопостоянства второй производной и интервалы выпуклости и вогнутости функции. Результаты сводим в таблицу.
| x | (0; 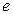 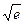 ) ) | (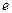 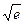 ;+¥) ;+¥) |
| y¢¢ | - | + |
| y | Ç | È |
Вторая производная меняет знак в точке х= 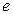
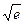 ,следовательно, эта точка является точкой перегиба. Вычислим значение функции в этой точке. Имеем
,следовательно, эта точка является точкой перегиба. Вычислим значение функции в этой точке. Имеем 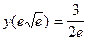 .
.
На основании проведенного исследования строим график функции.
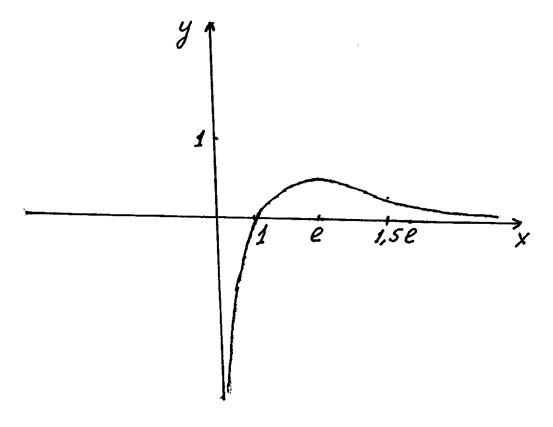
Задача 49. 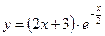
1. Область определения данной функции – вся числовая ось.
2. Четность, нечетность функции.
Имеем 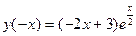 . Данная функция не является ни четной, ни нечетной.
. Данная функция не является ни четной, ни нечетной.
3.Нули, точки разрыва, точки пересечения графика с осями координат.
Поскольку данная функция элементарная и определена на всей числовой оси, то она непрерывна на всей числовой оси.
Для определения нулей функции решаем уравнение 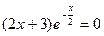 ; 2x+3=0;
; 2x+3=0; 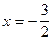 .
.
4.Интервалы знакопостоянства функции.
Функция может изменить знак только в одной точке 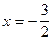 . Определим интервалы знакопостоянства функции.
. Определим интервалы знакопостоянства функции.
| x | 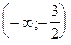 | 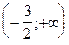 |
| y | - | + |
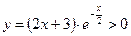 при
при 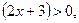
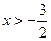 .
.
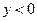 при
при 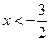 .
.
Найдем точки пересечения с осями:
y=3 при x=0, следовательно 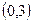 -- точка пересечения с осью
-- точка пересечения с осью 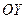 .
.
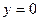 при
при 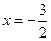 , следовательно
, следовательно 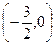 -- точка пересечения с осью
-- точка пересечения с осью 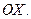
5а. Вертикальные асимптоты.
Поскольку функция непрерывна на всей числовой оси, то вертикальных асимптот нет.
5б. Наклонные асимптоты.
Учитывая разное поведение функции 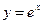 при
при 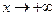 и при
и при 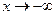 , будем искать асимптоты по отдельности для
, будем искать асимптоты по отдельности для 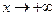 и
и 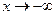 .
.
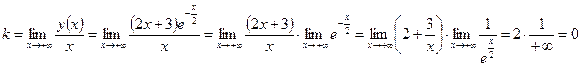 .
.
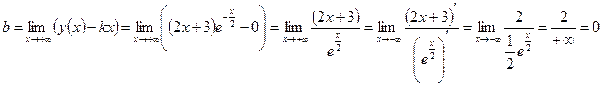 .
.
Отметим, что во втором пределе присутствует неопределенность вида 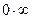 , которую мы обратили в неопределенность вида
, которую мы обратили в неопределенность вида 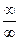 . Далее предел вычисляется по правилу Лопиталя, в соответствии с которым предел отношения при наличии неопределенности равен отношению производных числителя и знаменателя. Итак, при
. Далее предел вычисляется по правилу Лопиталя, в соответствии с которым предел отношения при наличии неопределенности равен отношению производных числителя и знаменателя. Итак, при 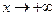 график исследуемой функции имеет горизонтальную асимптоту, совпадающую с осью
график исследуемой функции имеет горизонтальную асимптоту, совпадающую с осью 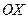 : y=0.
: y=0.
Выясним, существует ли наклонная асимптота при 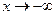 .
.
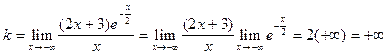
Поскольку коэффициент k не имеет конечного значения, делаем вывод о том, что график не имеет наклонной асимптоты при 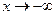 .
.
6. Интервалы возрастания, убывания функции. Точки экстремума.
Находим производную:
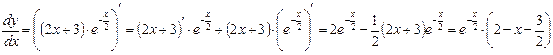
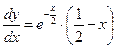 ,
, 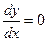 при
при  .
.
Точек разрыва производная не имеет. Определяем интервалы знакопостоянства первой производной и интервалы возрастания и убывания функции. Производная может изменить знак в единственной точке  . Составляем таблицу.
. Составляем таблицу.
| x | 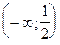 | 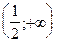 |
| y¢ | + | - |
| y |  |  |
Производная в точке  меняет знак с плюса на минус. Следовательно точка
меняет знак с плюса на минус. Следовательно точка  является точкой максимума функции. Вычислим значение функции в этой точке.
является точкой максимума функции. Вычислим значение функции в этой точке. 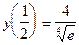 .
.
7. Выпуклость, вогнутость, точки перегиба графика функции.
Находим вторую производную
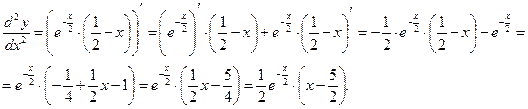
В области допустимых значений вторая производная точек разрыва не имеет. Вторая производная равна нулю при х= 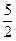 .
.
Определяем интервалы знакопостоянства второй производной и интервалы выпуклости и вогнутости функции.
Результаты сводим в таблицу.
| x | 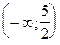 | 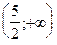 |
| y¢¢ | - | + |
| y | Ç | È |
Вторая производная меняет знак в точке х= 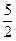 , следовательно эта точка является точкой перегиба. Вычислим значение функции в этой точке. Имеем
, следовательно эта точка является точкой перегиба. Вычислим значение функции в этой точке. Имеем 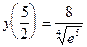 .
.
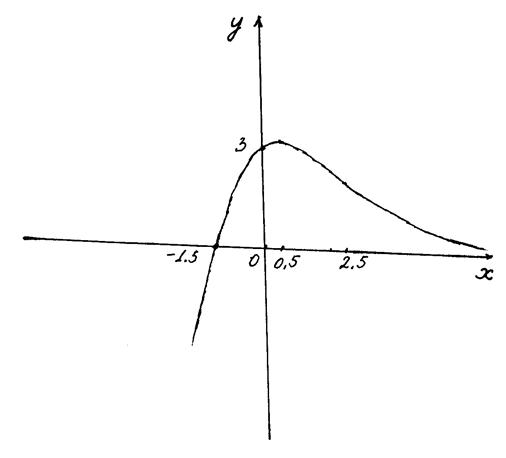
На основании проведенного исследования строим график функции.
 2015-04-20
2015-04-20 1486
1486