2015-04-30
566Приложим к рассмотренной выше раме, имеющей n динамических степеней свободы, возмущающую силу, изменяющуюся по гармоническому закону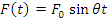 
, где 
- амплитуда, 
- частота изменения силы.
Конструкция начнет совершать свободные и вынужденные колебания, которые будут накладываться друг на друга. В силу наличия сил внешнего и внутреннего трения, собственные колебания быстро затухнут и система станет совершать установившиеся вынужденные колебания с частотой возмущающей силы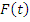 
. Все массы получат перемещения, изменяющиеся по гармоническому закону:
.
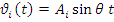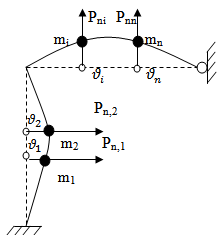
Найдем перемещение по направлению i степеней свободы:
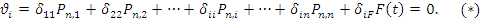
Силы инерции:
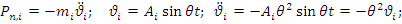
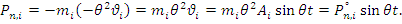
Где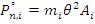 
- амплитудное значение силы инерции. Из выражения находим:
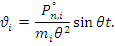
Подставляя силы инерции и перемещение в формулу (*), получаем:
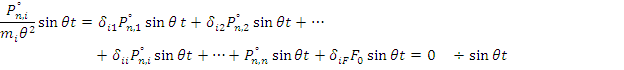
Обозначим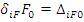 
- перемещение по направлению i степени свободы от статического действия силы, равной амплитуде возмущающей силы. Приведем подобные члены.
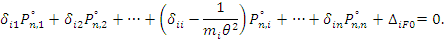
Раскрывая по всем i=1,2,…,n, получаем систему неоднородных алгебраических уравнений относительно амплитуд сил инерции.
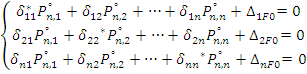
Здесь введено обозначение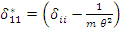 
- динамическая податливость. Она меньше статической податливости 
на величину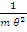 
и может быть как положительной, так и отрицательной.
Решая систему неоднородных уравнений, находим амплитудные значения сил инерции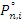 
. Затем строим окончательную динамическую эпюру изгибающих моментов:
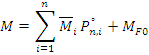
Где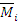 
, 
- единичная и грузовая эпюры моментов, которые строятся предварительно с целью определения коэффициентов при неизвестных.
Рассмотрим два частных случая:
а) система с одной степенью свободы.
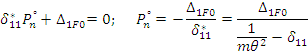
F(t)
m F(t) m
Если сила F(t) приложена к массе m, то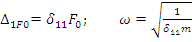 
откуда находим
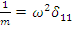. Следовательно, 
.
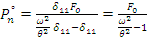Вычислим суммарную динамическую силу, которая складывается из силы инерции и возмущающей силы.
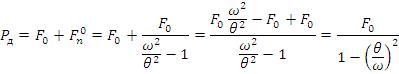
Обозначим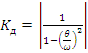 
- динамический коэффициент. Тогда получаем:
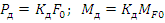– динамическая эпюра изгибающих моментов.
Покажем график изменения динамического коэффициента в зависимости от отношения вынужденной частоты колебания к собственной частоте колебания 
1
0 0.5 1 1.5 2 
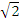
При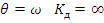 
- система приходит в состояние резонанса, т.е. теоретически она может быть разрушена при достаточно малой возмущающей силе 
.
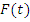В дорезонансном состоянии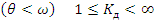 
.
В послерезонансном состоянии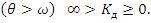 
Мы видим, что конструкция малочувствительна к высокочастотным колебаниям, которые называют вибрациями.
