Вопрос 17

СПИРАЛЬ КОРНЮ

КОРНЮ СПИРАЛЬ (по имени М. А. Корню, М. А. Соrnu) (клотоида) - кривая, используемая для графич. вычисления распределения интенсивности при дифракции света на прямолинейном крае или на щели (дифракция Фраунгофера); состоит из двух симметричных ветвей, бесконечное число раз обвивающихся вокруг "фокусов" F и и неограниченно приближающихся к ним.

Ур-ние К. с. в параметрич. форме имеет вид Френеля интегралов:

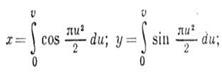
"фокусы" 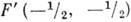и - асимптотич. точки кривой; пределы интегрирования определяются размерами щелей и экранов, на к-рых происходит дифракция.

Относит. амплитуда волны при дифракции на крае экрана зависит от длины вектора, проведённого из точки F в разл. точки К. с. (напр., М1М7). Скольжение вектора по правой (верх.) ветви спирали (FMl, FH2, FM3)определяет плавно уменьшающуюся амплитуду волны в области геом. тени; амплитуда на границе тени соответствует вектору FO; скольжение вектора по левой (ниж.) части спирали (FM4, FM5, FM6, FM7,)даёт дифракц. полосы в освещённой области. Амплитуда волны в отсутствие экрана или вдали от границы геом. тени определяется вектором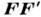

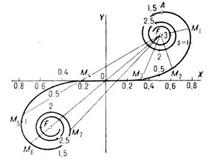
Дифракция на плоской щели

Распределение интенсивности света при дифракции на щели

В качестве примера рассмотрим дифракционную картину возникающую при прохождении света через щель в непрозрачном экране. Мы найдём интенсивность света в зависимости от угла в этом случае. Математическое представление принципа Гюйгенса используется для написания исходного уравнения.

Рассмотрим монохроматическую плоскую волну с амплитудой с длиной волны λ падающую на экран с щелью, ширина которой a.

Если разрез находится в плоскости x′-y′, с центром в начале координат, тогда может предполагаться, что дифракция производит волну ψ на расстоянии r, которая расходится радиально и вдалеке от разреза можно записать:

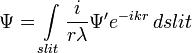
пусть (x′,y′,0) — точка внутри разреза, по которому мы интегрируем. Мы хотим узнать интенсивность в точке (x,0,z). Щель имеет конечный размер в x направлении (от до), и бесконечна в y направлении ([, ]).

Расстояние r от щели определяется как:

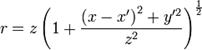
Предполагая случай дифракции Фраунгофера, получим условие. Другими словами, расстояние до точки наблюдения много больше характерного размера щели (ширины). Используя биноминальное разложение и пренебрегая слагаемыми второго и выше порядков малости, можно записать расстояние в виде:

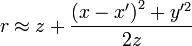
Видно, что 1/r перед уравнением не осциллирует, то есть даёт малый вклад в интенсивность по сравнению с экспоненциальным множителем. И тогда его можно записать приближённо как z.

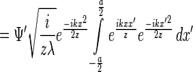
Здесь мы введём некую константу 'C', которой обозначим все постоянные множители в предыдущем уравнении. Она, в общем случае может быть комплексной, но это не важно, так как в конце нас будет интересовать только интенсивность, и нам будет интересен только квадрат модуля.