Задание к контрольной работе по теме 2.4

В задачах [3] 501 – 600 приведены таблицы, в клетках которых проставлены элементы матрицы эффективностей 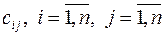задачи о разборчивой невесте. Необходимо найти оптимальный вариант выбора, при котором средняя продолжительность семейной жизни каждой семьи будет наибольшей. Решить задачу методом потенциалов и венгерским методом.

Вопросы для самопроверки

1. Сформулируйте задачу о назначениях как частный случай транс­портной задачи и запишите математическую модель.

2. Какие значения могут принимать переменные в задаче о назначениях?

3. Какие матрицы называются эквивалентными?

4. Сформулируйте предписания предварительного этапа венгерского метода решения задачи.

5. Сколько звездочек может быть в каждой строке и столбце матрицы эффективностей?

6. Что надо делать, если нет незанятых нулей?

7. Сколько нулей со штрихом может быть в одной строке?

8. Сколько нулей со штрихом может быть в одном столбце?

9. Что надо делать, если в строке, где находится только что отмечен­ный штрихом нуль, нет нуля со звездочкой?

10. Как преобразуется цепочка?

11. Сформулируйте задачу о разборчивой невесте.

12. Запишите оптимальный вариант выбора.

13. Как применяется метод Фогеля в задаче о разборчивой невесте?

14. Каковы особенности метода потенциалов для задачи о разборчивой невесте?

15. Какие значения может принимать величина корректировки в задаче с булевыми переменными?