4.1. Задайте матрицы системы – A и матрицу-столбец свободных членов – b.
4.2. Перейдите от исходной системы уравнений A · x = b к системе x = d + C · x.
4.3. Выполните проверку достаточного условия сходимости метода простой итерации.
4.4. Выберите начальное (нулевое) приближение, являющееся решением системы.
4.5. Задайте произвольное число итераций.
4.6. Используя начальное приближение и заданное количество итераций, найдите последующие приближения.
4.7. Оцените погрешность найденных приближений.
4.8. Сформулируйте выводы о справедливости найденных решений.
Пример выполнения работы
Пример 1. Задана система уравнений
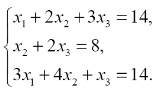
Найдите решение этой системы, используя функцию lsolve.
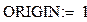
| данная функция показывает, что нумерация строк и столбцов матрицы начинается с единицы |
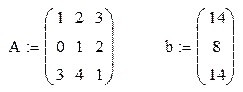
| формирование матрицы левой части системы – A и матрицы –столбца свободных членов b |
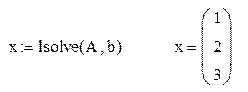
| поиск решения исходной системы уравнений и вывод его на печать |
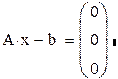
| проверка правильности решения |
Пример 2. Пусть задана система линейных алгебраических уравнений
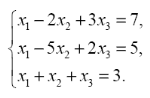
Найдите решение этой системы методом Гаусса.
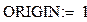
| данная функция показывает, что нумерация строк и столбцов матрицы начинается с единицы |
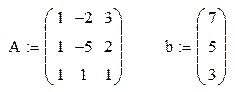
| формирование матрицы левой части системы – A и матрицы – столбца свободных членов b |
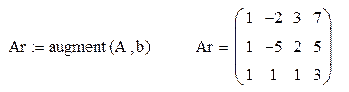
| формируется расширенная матрица системы уравнений, которая получается добавлением столбца свободных членов – функция augment |
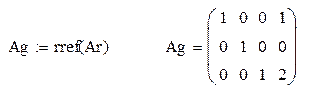
| приведение полученной расширенной матрицы к ступенчатому виду с помощью функции rref |
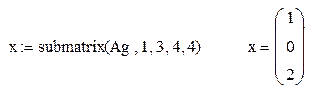
| при помощи функции submatrix выделяется столбец ступенчатой матрицы, содержащий решение исходной системы |
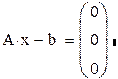
| проверка правильности решения |
Пример 3. Задана система линейных алгебраических уравнений
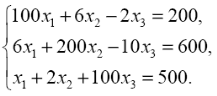
Найдите решение данной системы, используя метод простой итерации
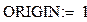
| данная функция показывает, что нумерация строк и столбцов матрицы начинается с единицы |
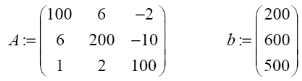
| формирование матрицы левой части системы – A и матрицы – столбца свободных членов b |
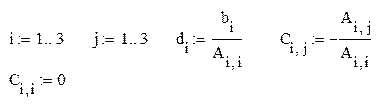
| переход от матриц, соответствующих исходной системе, к матрицам эквивалентной x = d + C*x |
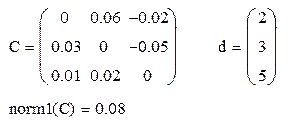
| проверка достаточного условия сходимости метода простой итерации: 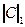
|
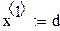
| задание нулевого (начального) приближения |
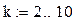
| определение количества итераций |
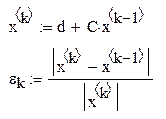
| вычисление последовательных приближений, начиная со второго, и погрешности для каждого из них |
Вывод последовательных приближений и погрешностей их вычисления
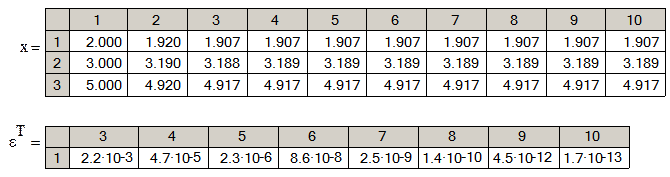
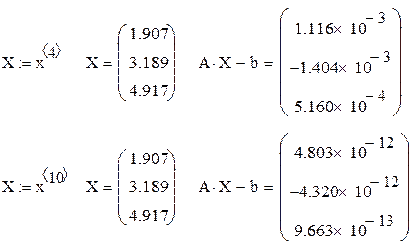
| проверка решения исходной системы линейных алгебраических уравнений и оценки погрешностей вычислений произвольных последовательных приближений |
Выводы: если приближенным решением считать 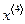 , то погрешность решения не превышает
, то погрешность решения не превышает 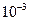 , а при
, а при 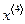 –
– 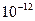 .
.
Варианты заданий
| Вариант | А) | Б) |
| 1. | 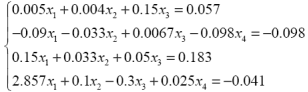
| 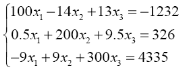
|
| 2. | 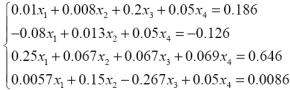
| 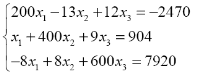
|
| 3. | 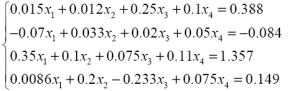
| 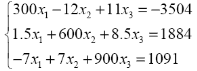
|
| 4. | 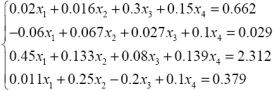
| 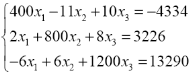
|
| 5. | 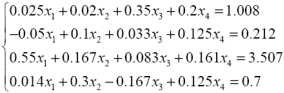
| 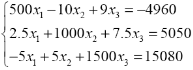
|
| 6. | 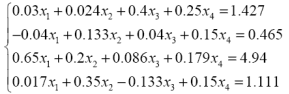
| 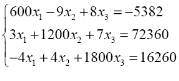
|
| 7. | 
| 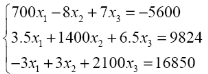
|
| 8. | 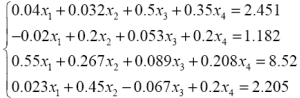
| 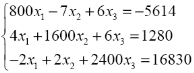
|
| 9. | 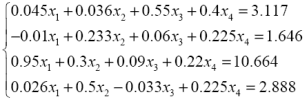
| 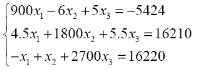
|
| 10. | 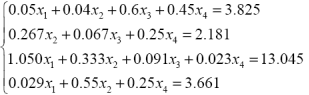
| 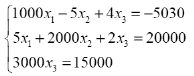
|
 2015-05-10
2015-05-10 533
533








