5.2. Проанализируйте описанный метод сортировки "пузырьком". Добавьте приведенный программный код в проект.
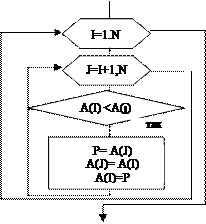
Рис.10.8 Схема алгоритма “ Метода пузырька".
Рассмотрим суть метода на примере. Пусть надо расставить по убыванию четыре числа:
Будем просматривать числа слева направо, очередное число будем сравнивать со следующим справа: если следующее число больше очередного, то поменяем их местами. Ниже для наглядности "очередное" число заключено в рамку.
Начинаем с самого левого числа:
Следующее число больше, значит, меняем их местами:
Переходим ко второму по счету числу:
Сравниваем его со следующим, оно больше, значит, меняем их местами:
Переходим к следующему, третьему, числу:
Сравниваем его со следующим, четвертым. Следующес больше, значит, меняем их местами:
На предпоследнем числе надо остановиться, так как если перейдем на последнее число, то его не с чем будет сравнивать — справа чисел нет.
Подведем итог: в результате одного просмотра самое маленькое число оказалась на последнем, своем законном, месте.
Самое большое число тоже находится на своем месте, где и положено быть. Однако это чистая случайность: результат того, что первоначально данное число стояло на втором месте; с любого другого места оно просто передвинулось бы на место левее. А вот самое маленькое число в конце просмотра обязательно окажется на последнем месте.
Повторим все сначала. Первое число сравниваем со вторым:
Второе не больше первого, поэтому их менять местами не будем, а просто переходим к следующему числу:
Сравниваем его со следующим; следующее больше предыдущего — значит, меняем их местами:
Переходим к следующему:
Сравниваем со следующим — менять не надо. Просмотр опять закончен, так как мы достигли предпоследнего числа. В результате второго просмотра второе по меньшинству число встало свое место — предпоследнее.
Нетрудно догадаться, что при третьем проходе третье по меньшинству число обязательно встанет на третье с конца место. То, что оно у нас встало на "свое" второе место уже при втором проходе, — тоже случайность, обусловленная первоначальным расположением чисел.
Четвертого прохода не требуется, так как если три числа встали на свое место, то четвертое окажется на своем месте автоматически.
Подведем итог: Если имеем массив из N элементов, то надо сделать N-1 проход по массиву от l -го до предпоследнего N-1 – гоэлемента. При каждом проходе надо текущий i- й элемент сравнивать со следующим (i + l) -м элементом, и если текущий элемент меньше следующего, необходимо менять их местами. Наверное, вы поняли, почему метод носит название "пузырька" —наименьший элемент как бы "всплывает" на свое последнее место.
 2015-05-14
2015-05-14 487
487








