Временным рядом (динамическим рядом) называется набор значений какого-либо показателя за несколько последовательных моментов или периодов времени. Отдельные наблюдения называются уровнями ряда.
В общем виде при исследовании экономических процессов временного ряда выделяются несколько составляющих:
yt = ut + vt + ct + εt (t= 1, 2, …, n),
где ut – тренд, vt – сезонная компонента, ct – циклическая компонента, εt – случайная компонента.
Стационарные временные ряды.
Важное значение в анализе временных рядов имеют стационарные временные ряды, вероятностные свойства которых не изменяются во времени. Временной ряд yt (t= 1, 2, …, n) называется строго стационарным, если совместное распределение вероятностей n наблюдений y1, y2,…, yn такое же, как и n наблюдений y1+τ, y2+τ,…, yn+τ при любых n, t, и τ. Таким образом, свойства строго стационарных рядов не зависят от момента времени t.
Степень тесноты связи между последовательностями наблюдений временного ряда y1, y2, …, yn и y1+τ, y2+τ, …, yn+τ можно оценить с помощью выборочного коэффициента корреляции r(τ):
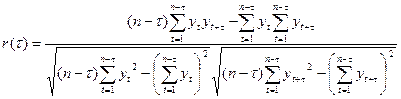 .
.
Так как он оценивает корреляцию между уровнями одного и того же ряда, его называют коэффициентом автокорреляции.
Функция r(τ) называется выборочной автокорреляционной функцией, а ее график - коррелограммой.
Кроме автокорреляционной функции при исследовании стационарных временных рядов рассматривают частную автокорреляционную функцию. Статистической оценкой частного коэффициента корреляции является выборочный частный коэффициент корреляции (или просто частный коэффициент корреляции):
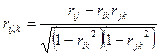 ,
,
где rij, rik rjk – выборочные коэффициенты корреляции.
Так, выборочный частный коэффициент автокорреляции 1-го порядка между членами временного ряда yt и yt+2 при устранении влияния yt+1 определяется по формуле:
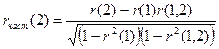 ,
,
где r(1), r(1,2), r(2) – выборочные коэффициенты автокорреляции между yt и yt+1, yt+1 и yt+2, и yt и yt+2 соответственно.
Наиболее распространенным приемом устранения автокорреляции во временных рядах является подбор соответствующей модели: авторегрессионной АР(p), скользящей средней СС(q) или авторегрегрессионной модели скользящей средней АРСС(p,q) для остатков модели (в литературе можно встретить англоязычные названия моделей: авторегрессионной – АR(p), скользящей средней – MA(q) и авторегрегрессионной модели скользящей средней АRMA(p,q).)
Идентификацией временного ряда называется построение для ряда остатков адекватной АРСС-модели, в которой остатки представляют собой белый шум, а все регрессоры значимы. Такое представление, как правило, не единственное, и один и тот же ряд может быть идентифицирован и с помощью АР-модели, и с помощью СС-модели.
Авторегрессионная модель порядка p (модель АР(p)) имеет вид:
yt = β0 + β1 yt-1+ β2 yt-2+…+ βp yt-p+εt, (t= 1, 2, …, n),
где β0, β1,… βp – некоторые константы.
Если исследуемый процесс yt в момент t определяется его значениями только в преды-дущий период t-1, то получаем авторегрессионную модель 1-го порядка (или модель АР(1)).
yt = β0 + β1 yt-1 +εt, (t= 1, 2, …, n),
Наряду с авторегрессионными моделями временных рядов в эконометрике рассматриваются также модели скользящей средней. В них моделируемая величина задается линейной функцией от возмущений (остатков) в предыдущие моменты времени. Модель скользящей средней порядка q (модель СС(q)) имеет вид:
yt = εt – γ1εt-1 – γ2εt-2 –…– γqεt-q (t= 1, 2, …, n).
Нередко используются и комбинированные модели временных рядов АР и СС, которые имеют вид:
yt = β0 + β1 yt-1+ β2 yt-2+…+ βp yt-p+ εt – γ1εt-1 – γ2εt-2 –…– γqεt-q.
Если все значения выборочной частной автокорреляционной функции порядка выше p незначимо отличаются от нуля, временной ряд следует идентифицировать с помощью модели, порядок авторегрессии которой не выше p.
Если все значения выборочной автокорреляционной функции порядка выше q незначимо отличаются от нуля, временной ряд следует идентифицировать с помощью модели скользящей средней, порядок которой не выше q.
Нестационарные временные ряды.
Пусть имеется временной ряд
yt = ρyt-1+ ξt.
Предположим, что ошибки ξt независимы и одинаково распределены, т.е. образуют белый шум. Перейдем к разностным величинам:
Δ yt = λyt-1+ ξt,
где Δ yt = yt – yt-1, λ= ρ-1.
Если ряд Δyt является стационарным, то исходный нестационарный ряд yt называется интегрируемым (или однородным).
Нестационарный ряд yt называется интегрируемым (однородным) k-го порядка, если после k -кратного перехода к приращениям
dkyt = dk-1yt – dk-1yt-1,
где d1yt = Δyt, получается стационарный ряд dkyt.
Если при этом стационарный ряд dkyt корректно идентифицируется как АРСС(p,q), то нестационарный ряд yt обозначается как АРПСС(p,k,q). Это означает модель авторегрессии – проинтегрированной скользящей средней (другое обозначение - ARIMA(p,k,q)) порядков p, k, q, которая известна как модель Бокса-Дженкинса. Процедура подбора такой модели реализована во многих эконометрических пакетах.
Модели с распределенными лагами.
При исследовании экономических процессов приходится моделировать ситуации, когда значение результативного признака в текущий момент времени t формируется под воздействием ряда факторов, действовавших в прошлые моменты времени. Величину l, характеризующую запаздывание в воздействии фактора на результат, называют лагом, а временные ряды самих факторных переменных, сдвинутые на один или более моментов времени, - лаговыми переменными. Модели, содержащие не только текущие, но и лаговые значения факторных переменных, называют моделями с распределенными лагами:
В случае конечной величины максимального лага модель имеет вид:
yt = a + b0xt + b1xt-1 + … + blxt-l + εt.
Коэффициент b0 характеризует среднее абсолютное изменение yt при изменении xt на 1 ед. своего измерения в некоторый фиксированный момент времени t, без учета воздействия лаговых значений фактора x. Этот коэффициент называется краткосрочным мультипликатором.
Долгосрочный мультипликатор вычисляется по формуле:
b = b0 + b1 + … + bl.
Он показывает абсолютное изменение в долгосрочном периоде t+l результата y под влиянием изменения на 1 ед. фактора x.
Величины βj = bj / b (j = 0,…, l) называются относительными коэффициентами модели с распределенным лагом.
Средний лаг определяется по формуле средней арифметической взвешенной:
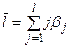
и представляет собой средний период, в течение которого будет происходить изменение результата под воздействием изменения фактора в момент времени t. Небольшая величина среднего лага свидетельствует об относительно быстром реагировании результата на изменение фактора. Высокое его значение говорит о том, что воздействие фактора на результат будет сказываться в течение длительного периода времени.
Медианный лаг (lMe) – представляет собой период времени, в течение которого буде реализована половина общего воздействия фактора на результат и определяется следующим соотношением:
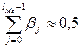 .
.
Оценка модели с распределенными лагами зависит от того, конечное или бесконечное число лагов она содержит.
Метод Алмон.
Предполагается, что веса текущих и лаговых значений объясняющих переменных подчиняются полиномиальному закону распределения:
bj = c0 + c1·j + c2·j2 + … + ck·jk. (5.1)
Уравнение регрессии примет вид:
yt = a + c0·z0 + c1·z1 + c2·z2 + … + ck·zk + εt, (5.2)
где 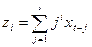 , i = 1,…, k; j =0,…, l. (5.3)
, i = 1,…, k; j =0,…, l. (5.3)
Схема расчета параметров модели:
1. устанавливается максимальная величина лага l;
2. определяется степень полинома k, описывающего структуру лага;
3. по соотношениям (5.3) рассчитываются значения переменных z0, z1,…, zk;
4. обычным методом наименьших квадратов определяются
параметры уравнения линейной регрессии yt от zi (5.2);
5. рассчитываются параметры исходной модели по формулам (5.1).
Метод Койка.
Предполагается, что коэффициенты при лаговых значениях переменной убывают в геометрической прогрессии:
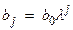 , j = 1, 2, … 0 < λ < 1. (5.4)
, j = 1, 2, … 0 < λ < 1. (5.4)
Уравнение регрессии преобразуется к виду:
yt = a + b0xt + b0·λ xt-1 + b0·λ2 xt-2 +… + εt.
После ряда преобразований получается уравнение авторегрессии первого порядка:
yt = a·(1 – λ) + b0·xt + (1 – λ) yt-1 + ut,
где ut = εt – λ εt-1.
Определив параметры данной модели, находятся λ и оценки параметров a и b0 исходной модели. Далее из соотношения (5.4) определяются параметры модели b1, b2,….
Величина среднего лага в модели Койка определяется формулой:
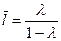 .
.
Пример 5. По данным о динамике товарооборота (Y, млрд. руб.) и доходах населения (X, млрд. руб.) была получена следующая модель с распределенными лагами:
Yt = 0,50∙ Xt + 0,25∙ Xt-1 + 0,13∙ Xt-2 + 0,13∙ Xt-3 + εt.
(0,06) (0,04) (0,04) (0,06)
В скобках указаны значения стандартных ошибок для коэффициентов регрессии. Значение R 2 = 0,98.
Задание:
1. Проанализируйте полученные результаты регрессионного анализа.
2. Дайте интерпретацию параметров модели: определить краткосрочный и долгосрочный мультипликаторы.
3. Определите величину среднего лага и медианного лага.
Решение.
1. Проверка значимости отдельных коэффициентов модели дает следующие расчетные значения t-статистики для коэффициентов:
tb0 = 0,50/0,06 = 8,33; tb1 = 0,25/0,04 = 6,25;
tb2 = 0,13/0,04 = 3,25; tb3 = 0,13/0,06 = 2,17.
Таким образом, все коэффициенты оказываются значимыми, и выбор величины лага l =3 является оправданным. Об адекватности полученной модели свидетельствует и высокое значение коэффициента детерминации.
2. Краткосрочный мультипликатор в модели равен b0 = 0,50. Он показывает, что увеличение доходов на 1 млрд. руб. ведет в среднем к росту товарооборота на 0,5 млрд. руб. в том же периоде.
Долгосрочный мультипликатор для полученной модели составит:
b = b0 + b1 + b2 + b3 = 0,50 + 0,25 + 0,13 + 0,13 = 1,01.
Получаем, что увеличение доходов на 1 млрд. руб. в настоящий момент времени в долгосрочной перспективе (через 3 месяца) приведет к росту товарооборота на 1,01 млрд. руб.
Рассчитаем относительные коэффициенты модели:
β0 = 0,50/1,01 = 0,495; β1 = 0,25/1,01 = 0,248;
β2 = 0,13/1,01 = 0,129; β3 = 0,13/1,01 = 0,129.
Следовательно, 49,5% общего увеличения товарооборота, вызванного ростом доходов населения, происходит в текущий момент времени; 24,8% - в момент времени (t +1); 12,9% - в моменты времени (t +2) и (t +3).
3. Средний лаг в модели определяется следующим образом:
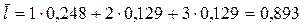 .
.
Величина среднего лага меньше месяца, что подтверждает, что эффект роста доходов населения на объем товарооборота проявляется сразу же.
Медианный лаг для данной модели составляет чуть более 1 месяца. ¨
 2015-05-18
2015-05-18 650
650








