Контрольная работа

Задание 1. Задача №4(N=4). Линейная регрессия.

Заданы выборочные данные, состоящие из 15 значений некоторого фактора Х, который влияет на показатель Y:

№
X	2,07 +N	3,04 +N	3,22 +N	3,42 +N	5,23 +N	5,7 +N	6,34 +N	6,41 +N	6,53 +N	6,68 +N	6,83 +N	7,19 +N	7,46 +N	8,19 +N	9,72 +N
Y	22,68	23,89	24,32	25,97	26,23	27,6	28,13	29,84	30,31	31,52	32,27	33,77	34,66	35,93	36,97

1) По выборочным данным построить выборочную линию регрессии Y на X.

2) По результатам визуального анализа определить вид модели - теоретической зависимости y = f (x).

3) Определить параметры модели.

4) Проверить качество модели визуально (построив теоретическую линию регрессии на диаграмме с выборочной линией), количественно (с помощью коэффициента детерминации) и статистически (с помощью критерия Фишера, α = 0,05).

5) Выполнить точечный и интервальный прогноз по заданному 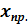= 8,71.

Решение:

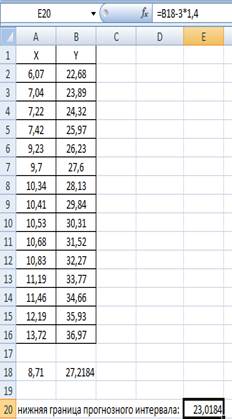
1) Введем выборочные данные в лист Excel:

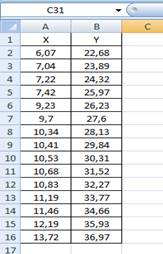
Изобразим полученную зависимость графически точками координатной плоскости по данным значений X и Y:

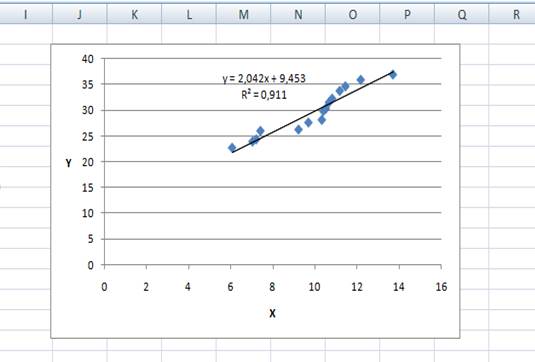
2) Выберем линейную функцию в качестве теоретического уравнения регрессии:

.

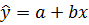3) Построение линейной регрессии сводится к оценке ее параметров – a и b. Параметры линейной регрессии a и b найдемc помощью метода наименьших квадратов (МНК).

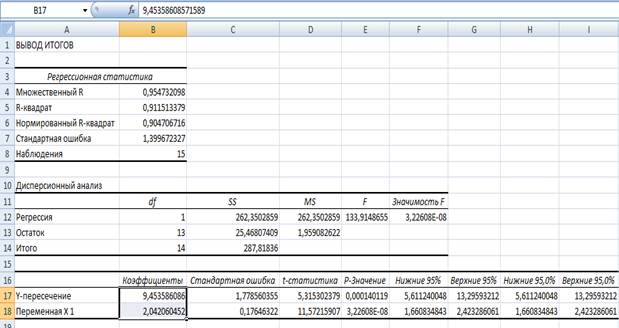
Уравнение регрессии имеет вид:

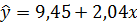
4) Коэффициент детерминации .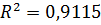

На 91,15% изменение фактора Y определяет тот фактор Х, который вошел в уравнениe регрессии.

Расчетное значение критерия Фишера 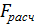= 133,91 (по данным таблицы).

Расчетное значение критерия Фишера сравниваем с табличным. Табличное значение найдем с помощью статистической функции FРАСПОБР.

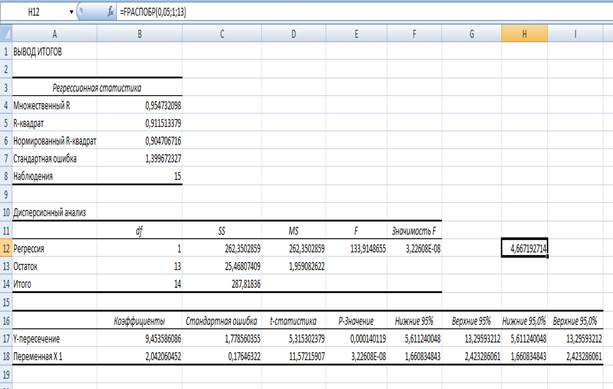
Табличное значение = 4,67.

Так как , делаем вывод о том, что с надежностью 0,95 модель адекватна эмпирическим данным.

5) Выполним точечный прогноз регрессанта при 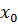=8,71:

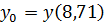= 9,45 + 2,04 * 8,71 = 27,22

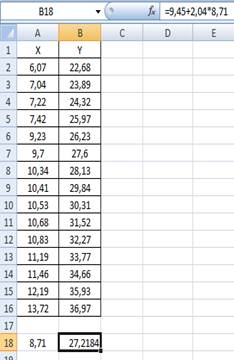
σ 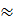1,40, где σ - стандартная ошибка.

Найдем значение нижней и верхней границ прогнозного интервала: .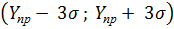

Нижняя граница прогнозного интервала:

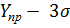= 27,2184 - 3 * 1,4 = 23,0184.

Верхняя граница прогнозного интервала:

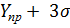= 27,2184 + 3 * 1,4 = 31,4184.

Вывод: с надежностью 0,95 прогнозное значение фактора Y будет находиться в пределах от 23,0184 до 31,4184.

Задание 2. Задача 19(N = 9).Нелинейная регрессия.

Для изучения изменения товарооборота (y, тыс. грн) со временем t (годы):

1) Построить эмпирическую линию регрессии и выбрать тренд.

2) Найти параметры корреляционного уравнения.

3) Решить проблему адекватности модели α=0,05.

4) Решить проблему тесноты связи, используя коэффициент корреляции.

5) Решить проблему точечного и интервального прогноза на 2015 год.

N	Объем товарооборота

Решение:

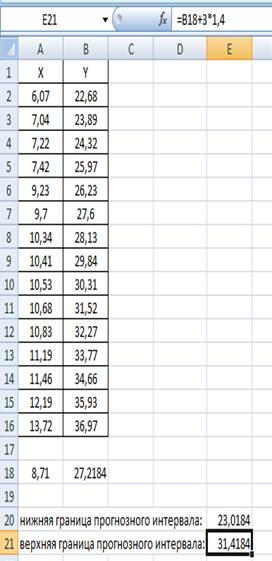
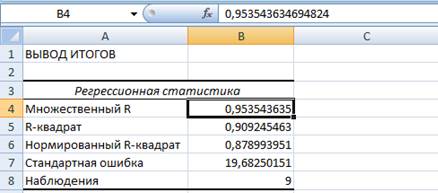
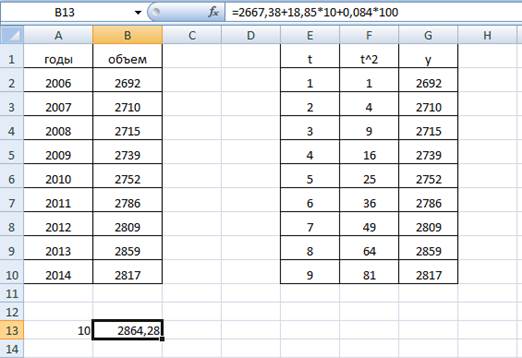
1) Введем эмпирические данные в лист Excel:

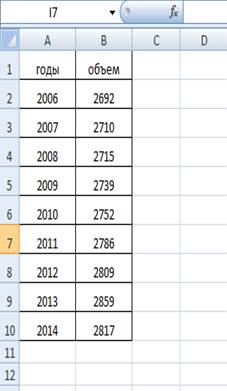
Вставим график по данным значения объема товарооборота:

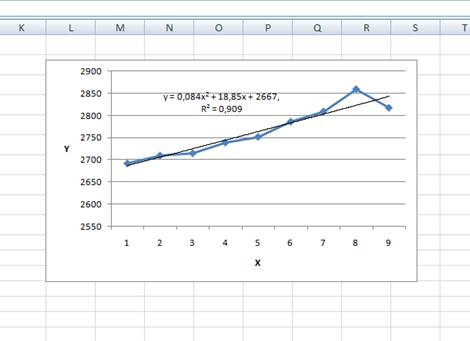
2) Сравнив коэффициенты детерминации разных линий тренда выберем полином второй степени:

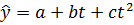
Для того, чтобы провести анализ модели проведем замену: ; .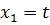

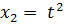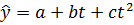
Вставим значения в лист Excel:

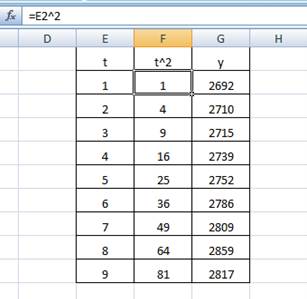
Найдем параметры корреляционного уравнения:

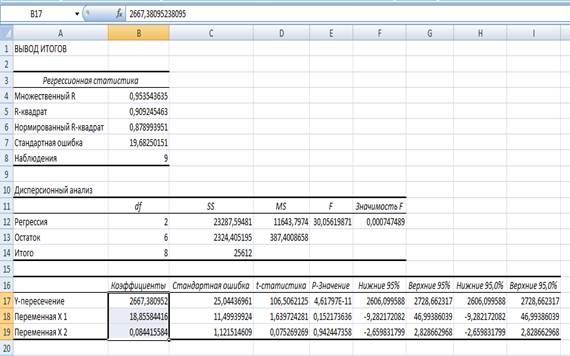
a = 2667,38; b = 18,85; c = 0,084.

Произведем обратную замену:

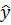= 2667,38 + 18,85 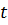+ 0,084 .

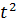Коэффициент детерминации 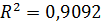означает, что изменение товарооборота на 90,92% описывается уравнением регрессии.

3) Расчетное значения критерия Фишера 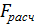= 30,06 (по данным таблицы).

Расчетное значение критерия Фишера сравниваем с табличным. Табличное значение найдем с помощью статистической функции FРАСПОБР.

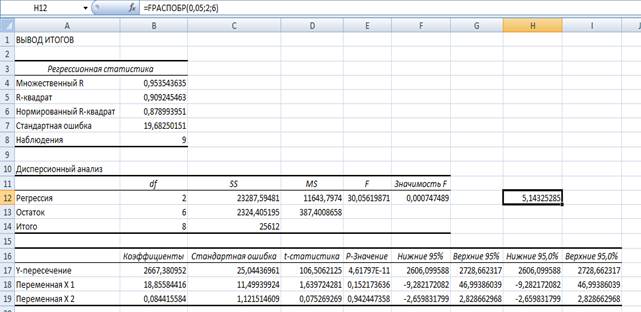
Табличное значение = 5,14.

Так как , делаем вывод о том, что с надежностью 0,95 модель адекватна эмпирическим данным.

4) Так как коэффициент корреляции r 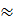0,95, то это означает, что зависимость товарооборота от времени очень тесная.

5) Выполним точечный прогноз товарооборота на 2015 год.

t = 10, , .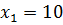

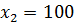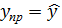(10;100) = 2667,38 + 18,85 * 10 + 0,084 * 100 = 2864,28.

σ 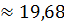где σ - стандартная ошибка.

Найдем значение нижней и верхней границ прогнозного интервала:

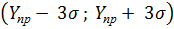
Нижняя граница прогнозного интервала:

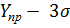= 2864,28 - 3 * 19,68 = 2805,24.

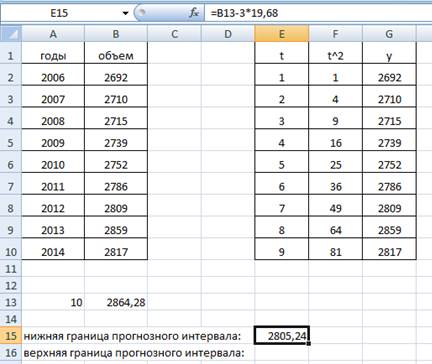
Верхняя граница прогнозного интервала:

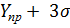= 2864,28 + 3 * 19,68 = 2923,32

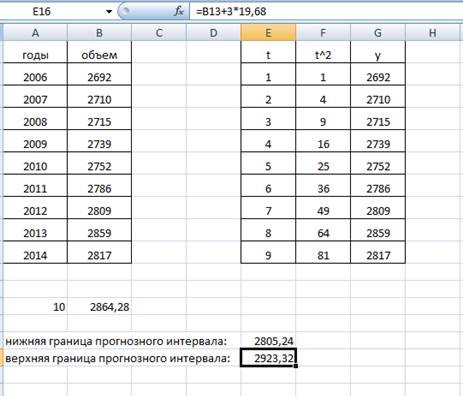
Вывод. В 2014 году среднее значение прогноза товарооборота 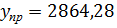с надежностью 0,95 будет находиться в пределах от 2805,24 до 2923,32 тыс.грн.

Задание 3. (Задачи 21-30) Производственная функция.

Эмпирические данные по 15 однотипным предприятиям представлены в виде таблицы:

N=3	K	54,2	56,8	59,7	61,4	63,5	64,7	64,8	67,4	69,0	70,7	71,3	73,7	75,9	76,2	76,5	77,5
L	33,6	39,1	40,4	42,9	44,0	46,8	51,9	56,3	56,6	58,7	59,6	62,4	63,9	64,4		67,2
V	85,1	95,4	98,5	102,7	105,2	109,5	116,2	123,2	124,5	128,1	128,7	133,0	137,4			?

В качестве единицы измерения производственных фондов К выбранное количество единиц оборудования, вложенного труда, L - количество человеко-часов, объем производства V измеряют в денежных единицах.

1) Пользуясь эмпирическими данными, построить эконометрическую модель Кобба-Дугласа V =А⋅ .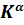

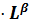2) С помощью критерия Фишера для уровня значимости α = 0,05 проверить адекватность найденной модели.

3) С помощью критерия Стьюдента определить значимость регрессоров.

4) Найти средние и предельные эффективности производственных факторов, предельные нормы взаимозамещения факторов, фондоемкость, трудоемкость для N-го предприятия.

5) Найти эластичность выпуска по основным производственным фондам и по затратам труда.

6) Сделать точечный и интервальный прогнозы.

Решение:

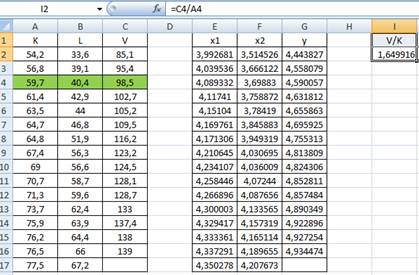
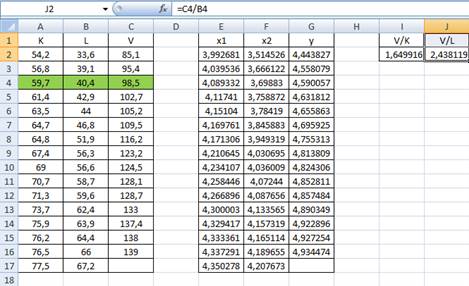
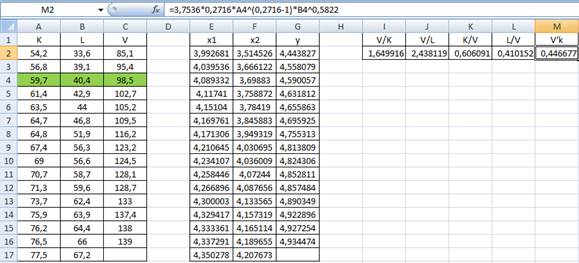
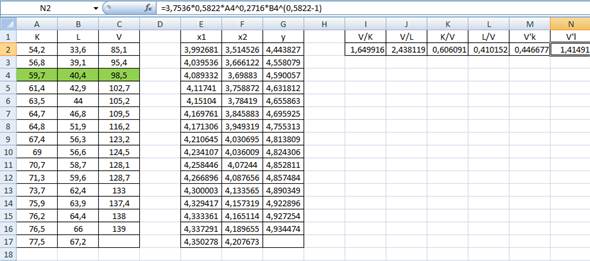
1) Введем эмпирические данные по 15 предприятиям в лист Excel:

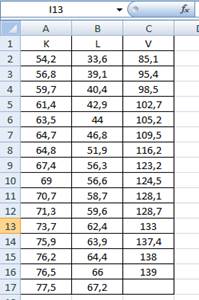
В качестве единицы измерения K выбрано количество единиц оборудования, L- количество человеко-часов, V измеряют в денежных единицах.

Найдем производственную функцию Кобба-Дуглас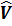а:

=А⋅ .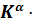

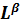Чтобы свести нашу задачу к построению линейной модели, прологарифмируем:

.

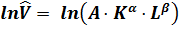По свойствам логарифмов, получаем:

.

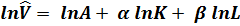Выполняя замену

y = 𝑙𝑛V; a = 𝑙𝑛A; ; .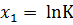

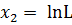сведем нелинейную функцию к линейной,

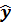= a + α 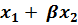-- линейная функция.

Таким образом, получаем следующую таблицу:

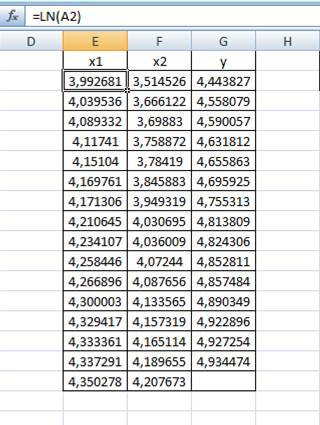
Далее найдем параметры a, α, β:

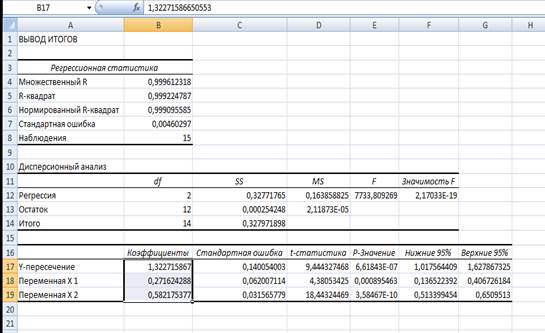
a = 1,3227;

α = 0,2716;

β = 0,5822.

Найденные значения подставим в линейную функцию 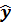= a + α .

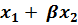Получим уравнение тренда линеаризированной модели (линейное уравнение регрессии):

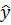= 1,3227 + 0,2716 .

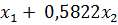Производим обратную замену:

A =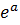

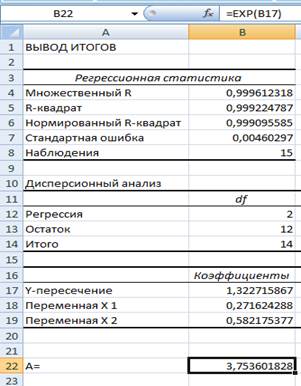
A =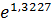

A = 3,7536.

Производственная функция Кобба-Дугласа имеет вид:

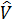=3,7536 ⋅ .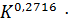

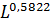2) С помощью критерия Фишера для уровня значимости α = 0,05 проверим адекватность построенной модели эмпирическим данным.

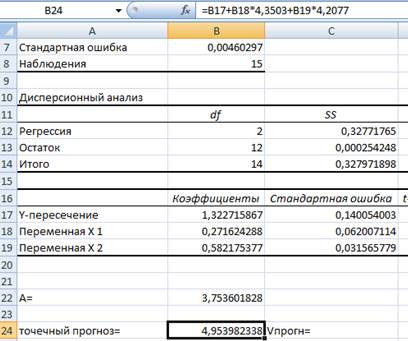
Расчетное значение критерия Фишера 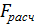= 7733,8 (по данным таблицы).

Расчетное значение критерия Фишера сравниваем с табличным. Табличное значение найдем с помощью статистической функции FРАСПОБР.

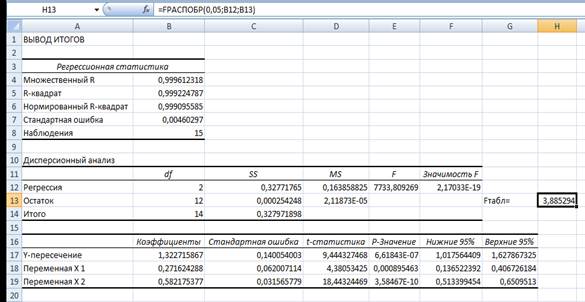
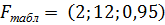= 3,88.

Так как , делаем вывод о том, что с надежностью 0,95 модель адекватна эмпирическим данным.

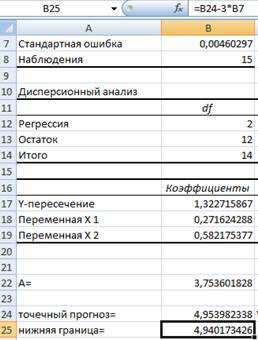
3) С помощью критерия Стьюдента определим значимость регрессоров.

Расчетные значения критерия Стьдента (по данным таблицам):

;

.

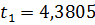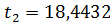Расчетные значения критерия Стьдента сравниваем с табличным. Табличное значение найдем с помощью статистической функции СТЬЮДРАСПОБР.

.

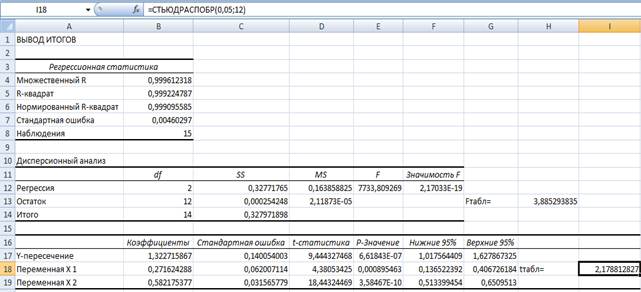
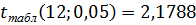Так как 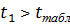, то первый регрессор, а именно количество единиц оборудования является значимым.

Так как 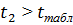, то второй регрессор, а именно количество человеко-часов также является значимым.

4) Найдем экономические показатели для третьего предприятия, которые можно вычислить с помощью производственной функции:

V = .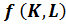

a) Средняя фондоотдача :

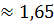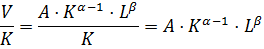
На единицу оборудования приходится приблизительно 1,65 единиц произведенной продукции.

б) Средняя производительность труда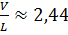

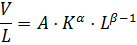
На один человеко-час приходится 2,44 единицы продукции.

в) Предельная фондоотдача 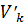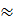0,45

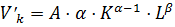
При увеличении (уменьшении) количества единиц оборудования на единицу объем произведенной продукции увеличится (уменьшится) приблизительно на 0,45 единиц.

г) Предельная производительность труда 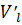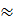1,41

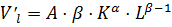
При увеличении (уменьшении) рабочего времени на единицу объем произведенной продукции увеличится (уменьшится) приблизительно на 1,41 единицу.

д) Фондоемкость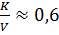

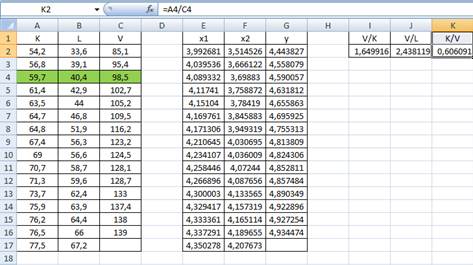
На единицу произведенной продукции приходится приблизительно 0,6 единиц оборудования.

е) Трудоемкость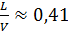

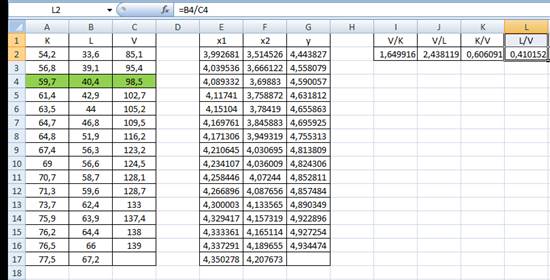
На единицу произведенной продукции приходится приблизительно 0,41 единиц человеко-часов.

ё) Предельная норма замещения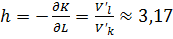

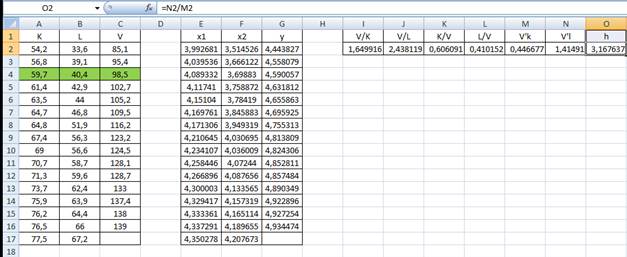
Если уменьшить рабочее время на единицу, то количество единиц оборудования необходимо увеличить приблизительно на 3,17 единиц для того, чтобы объем произведенной продукции оставался неизменным.

5) Эластичность выпуска продукции по производственным фондам:

.

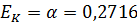Если количество единиц оборудования увеличить (уменьшить) на 1%, то объем произведенной продукции увеличится (уменьшится) приблизительно на 0,2716%.

Эластичность выпуска продукции по затратам труда:

.

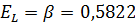Если количество рабочего времени увеличить (уменьшить) на 1%, то объем произведенной продукции увеличится (уменьшится) приблизительно на 0,5822%.

6) Для прогнозных значений K и L вычислим соответствующие значения 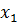и .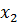

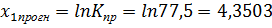
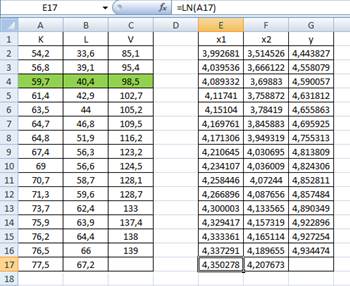
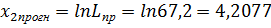
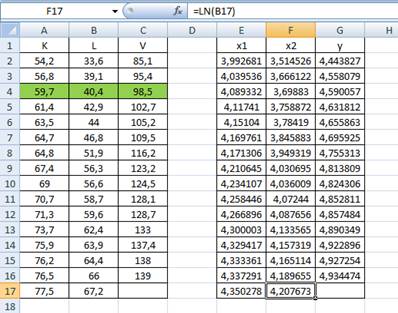
Подставив эти значения в линейное уравнение регрессии, получим точечную оценку:

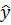= 1,3227 + .

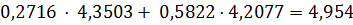Найдем значение нижней и верхней границ прогнозного интервала:

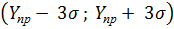, где σ 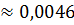где σ - стандартная ошибка.

Нижняя граница прогнозного интервала:

.

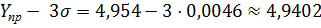Верхняяя граница прогнозного интервала:

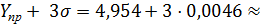4,9678.

Найдем значение нижней и верхней границ от точечного прогноза с помощью функции EXP:

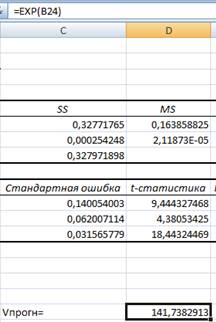
Нижняя граница 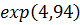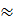139,79:

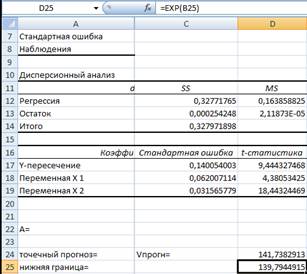
Верхняя граница 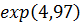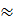143,71:

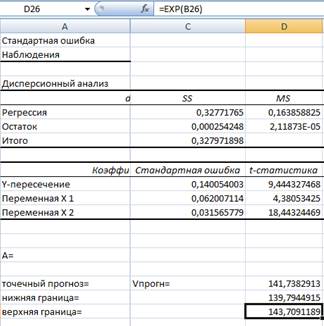
Вывод. С надежностью 0,95 можно утверждать, что для рассматриваемого предприятия среднее значение объема произведенной продукции 141,74 денежных единиц находится в пределах от 139,79 денежных единиц до 143,71 денежных единиц.