Сезонными называются периодические колебания, возникающие под влиянием смены времени года. Их роль очень велика в агропромышленном комплексе, в торговле многими товарами, в заболеваемости, в строительстве, в деятельности рекреационных учреждений, на транспорте. Сезонные колебания строго цикличны – повторяются через каждый год, хотя сама длительность времен года имеет колебания. Для изучения сезонных колебаний необходимо иметь уровни за каждый квартал, а лучше за каждый месяц, иногда даже за декады, хотя декадные уровни могут уже сильно исказиться мелкомасштабной случайной колеблемостью.
Для учета сезонных колебаний в модели динамики используется следующая методика.
1. По месячным или квартальным уровням за ряд лет вычисляется тренд (уравнение и выровненные по нему уровни для каждого месяца (или квартала) - 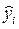 ).
).
2. Фактические уровни делятся на соответствующие уровни тренда, получаются "индексы сезонности": 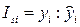 (4).
(4).
3. Эти индексы сезонности для каждого месяца или квартала усредняются за все годы, при этом нужно вычислять взвешенные средние. Весами являются средние месячные или квартальные уровни каждого года.
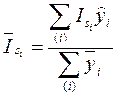 (5).
(5).
4. Уровни тренда умножаются на средние индексы сезонности соответствующих методов (кварталов). Получаем уровни тренда с учетом сезонной волны 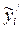 для каждого месяца (квартала):
для каждого месяца (квартала):
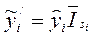 (6).
(6).
Показатели сезонной колеблемости можно получить как за каждый год в отдельности, так и в среднем за все годы. Покажем расчет на примере динамики реализации сельскохозяйственной продукции по кварталам за три года (табл. 10). Будем считать тренд линейным.
Таблица 10
Расчетная таблица
| Годы | Кварталы | Уровни
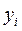
| Тренд
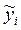
| Индексы сезонности
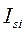
| Тренд с учетом сезонности
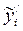
|
| I | 1. | 1,226 | |||
| 2. | 0,757 | ||||
| 3. | 0,837 | ||||
| 4. | 1,184 | ||||
| II | 1. | 1,164 | |||
| 2. | 0,82 | ||||
| 3. | 0,836 | ||||
| 4. | 1,178 | ||||
| III | 1. | 1,228 | |||
| 2. | 0,835 | ||||
| 3. | 0,824 | ||||
| 4. | 1,124 | ||||
| Сумма | - | 12,0 |
По данным таблицы 4 уравнение тренда 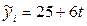 , где
, где 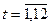
Взвешенные индексы сезонности составляют:
для I квартала: 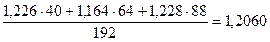 ;
;
для II квартала: 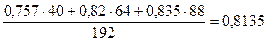 ;
;
для III квартала: 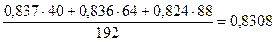 ;
;
для IV квартала: 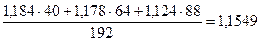 .
.
Умножив уровни тренда соответствующих кварталов на эти средние индексы сезонности получаем уровни, учитывающие и тренд, и сезонные колебания, обозначенные как 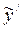 .
.
 2015-05-18
2015-05-18 625
625








