Коэффициент гидравлического трения по длине (Дарси)

Для ламинарного режима движения в круглой трубе коэффициент 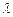определяется по теоретической формуле:

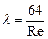, (4.7)

а для труб любой формы сечения:

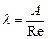, (4.8)

где 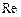- число Рейнольдса,

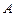- коэффициент формы.

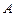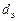Значения для и определяются по таблицам.

При турбулентном режиме движения коэффициент 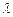зависит в общем случае от числа Рейнольдса 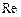и относительной шероховатости 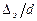(где 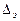- эквивалентная шероховатость) и определяется по эмпирическим формулам. При этом различают три области гидравлических сопротивлений - гидравлически гладких труб (русел), доквадратичного и квадратичного сопротивления.

Трубы называются гидравлически гладкими, когда толщина ламинарной пленки у стенки 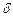, больше абсолютной шероховатости 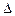. В этом случае шероховатость скрыта под ламинарной пленкой и не влияет на движение. С увеличением числа Re ламинарная пленка становится тоньше, и, когда шероховатость полностью «обнажается», т.е. начинает омываться турбулентным ядром потока, труба становится гидравлически шероховатой.

При турбулентном режиме в области гидравлически гладких русел, когда

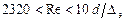
коэффициент трения зависит только от числа Рейнольдса и определяется по формуле Блазиуса (1913 г.):

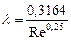. (4.9)

Для турбулентного режима движения в доквадратичной области сопротивления, когда

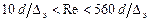
коэффициент трения зависит и от числа Рейнольдса и от относительной шероховатости. Для этой области сопротивления может быть рекомендована формула А.Д. Альтшуля

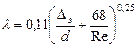. (4.10)

Наиболее значимой для расчетов является квадратичная область сопротивлений, которая наступает при числах Рейнольдса

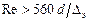
В этой области коэффициент 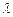зависит только от относительной шероховатости и может определятся по формуле Б.Л. Шифринсона

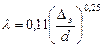. (4.11)

При ламинарном движении жидкости в круглых трубах потери напора и давления можно также определить по формулам Пуазейля:

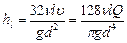, и 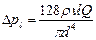(4.12)

где 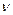- кинематическая вязкость;

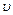- средняя скорость;

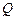- расход жидкост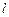и;

и 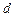- длина и диаметр трубы.

Местные потери напора в общем случае вычисляются по формуле Ю. Вейсбаха:

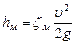, (4.13)

где 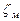- коэффициент местного сопротивления, зависящий от вида местного сопротивления.

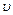- скорость после местного сопротивления.

В большинстве случаев коэффициент 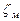определяют по справочным данным, полученным на основании опытных данных. При внезапном расширении русла коэффициент сопротивления при турбулентном движении определяется по формуле:

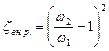, (4.14)

При внезапном (резком) сужении от сечения с площадью 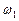до 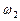коэффициент сопротивления на внезапное сужение определяется по формуле:

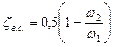. (4.15)