Под сложными трубопроводами понимают систему трубопроводов, имеющих ответвления, параллельные или кольцевые участки, переменный расход и т. д.
При последовательном соединении трубопроводов различного диаметра (рис. 5.2, а) исходят из того, что полные потери напора в трубопроводе равны сумме потерь напора на отдельных его участках (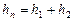 ).
).
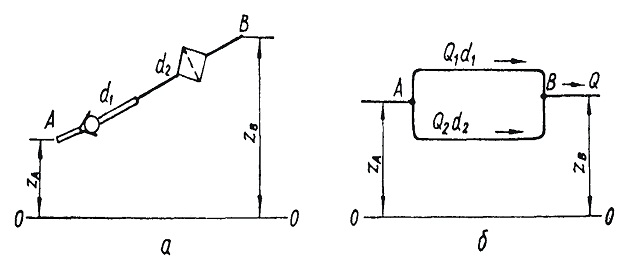 Рисунок 5.2 Схемы сложных трубопроводов:
Рисунок 5.2 Схемы сложных трубопроводов:
а) при последовательном соединении; б) при параллельном соединении
Расчет таких трубопроводов целесообразно производить графоаналитическим способом с использованием графиков зависимости потерь напора от расхода (рис. 5.3, а). Задаются значениями 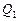 ,
, 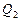 ,...,
,..., 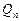 <
< 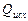 <
< 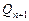 ,
, 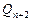 ,...,
,..., 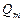 . Для каждого значения
. Для каждого значения 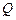 строят кривые для заданных трубопроводов 1 и 2 (для заданной схемы), используя зависимость для определения потерь напора на
строят кривые для заданных трубопроводов 1 и 2 (для заданной схемы), используя зависимость для определения потерь напора на 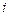 -том участке:
-том участке:
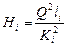 , при
, при 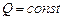 (5.8)
(5.8)
где 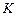 - расходная характеристика трубопровода, т. е. расход при
- расходная характеристика трубопровода, т. е. расход при 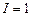 (
(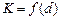 ).
).
Кривую 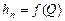 строят сложением ординат кривых
строят сложением ординат кривых 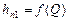 и
и 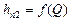 . По
. По 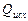 и кривой
и кривой 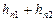 определяют полные потери напора в трубопроводе
определяют полные потери напора в трубопроводе 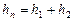 .
.
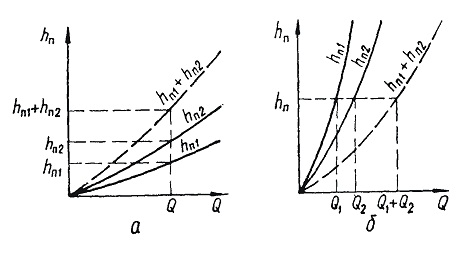
Рисунок 5.3 – К расчету сложных трубопроводов:
а) при последовательном соединении; б) при параллельном соединении
При расчете трубопроводов с параллельными ветвями (рис. 5.2, б) исходят из того, что сумма расходов в отдельных ветвях равна полному расходу (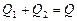 ) и что потери напора во всех ветвях одинаковы
) и что потери напора во всех ветвях одинаковы 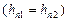 .
.
Задаются значениями 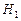 ,
,  ,...,
,..., 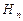 <
< 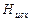 <
< 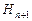 ,
, 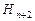 ,...,
,..., 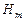 . Для каждого значения
. Для каждого значения 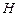 строят кривые для заданных трубопроводов 1 и 2 (для заданной схемы), используя зависимость для определения расхода на
строят кривые для заданных трубопроводов 1 и 2 (для заданной схемы), используя зависимость для определения расхода на 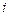 -том участке:
-том участке:
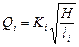 , при
, при 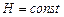 . (5.9)
. (5.9)
Зависимость полного расхода 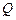 на разветвленном участке от потерь напора
на разветвленном участке от потерь напора 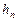 строится сложением абсцисс кривых
строится сложением абсцисс кривых 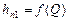 и
и 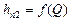 (рис. 5.3, б). По
(рис. 5.3, б). По 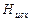 и кривой
и кривой 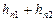 определяют расход
определяют расход 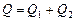 в трубопроводе.
в трубопроводе.
ПРИМЕР. Рассмотрим схему решения одной из задач на расчет разветвленного трубопровода.
Пусть тупиковый трубопровод (рис. 5.4) имеет всего три участка, где 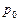 ,
, 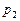 и
и 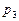 - давления в его конечных точках;
- давления в его конечных точках;
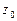 ,
, 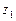 ,
, 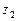 и
и 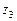 - расстояние этих точек от горизонтальной плоскости сравнения.
- расстояние этих точек от горизонтальной плоскости сравнения.
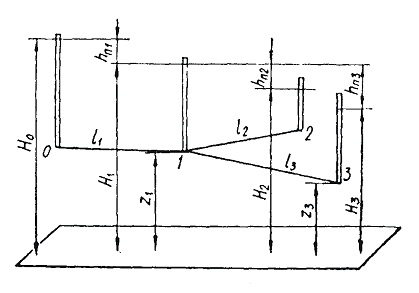
Рисунок 5.4 Схема тупикового трубопровода с тремя участками
В зависимости от соотношения между пьезометрическими напорами:
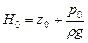 ,
, 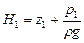 ,
, 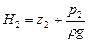 ,
, 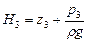
направление движения жидкости в трубопроводах может быть различным.
Рассмотрим случай, когда 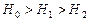 , и
, и 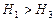 . Определим полный расход жидкости в трубопроводе
. Определим полный расход жидкости в трубопроводе 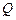 и расходы в отдельных его ветвях
и расходы в отдельных его ветвях 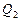 и
и 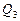 при заданных геометрических размерах трубопроводов (
при заданных геометрических размерах трубопроводов (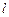 ,
, 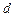 ,
, 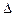 ), отметках характерных точек
), отметках характерных точек 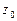 ,
, 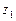 ,
, 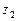 ,
, 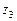 и давлениях в начальной точке (
и давлениях в начальной точке (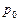 ) и конечных точках (
) и конечных точках (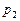 и
и 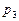 ).
).
Для решения задачи воспользуемся системой уравнений, связывающих искомые расходы 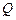 ,
, 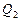 и
и 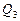 и потери напора на отдельных участках трубопровода:
и потери напора на отдельных участках трубопровода:
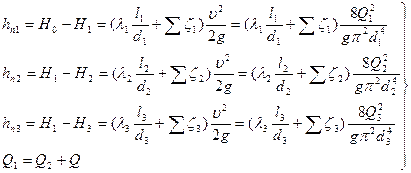 . (5.10)
. (5.10)
Решение системы уравнений (5.10) целесообразно выполнить графоаналитическим способом. Представим три уравнения системы (5.10) для трубопроводов 1,2,3 соответственно:
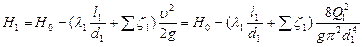 ;
;
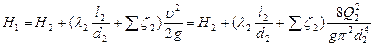 ;
;
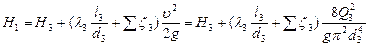 .
.
По этим формулам построим графики зависимости пьезометрического напора в узле 1 от расхода (рис. 5.5) для всех трубопроводов (кривые 1, 2 и 3).
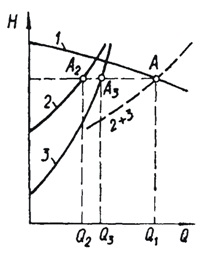
Рисунок 5.5 - Графики зависимости пьезометрического напора от расхода
Зависимость суммарного расхода в трубопроводах 2 и 3 от напора 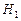 (кривая 2 + 3) строится сложением абсцисс кривых 2 и 3.
(кривая 2 + 3) строится сложением абсцисс кривых 2 и 3.
Значение напора 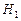 при котором суммарный расход в трубопроводах 2 и 3 равен расходу в трубопроводе 1, и является искомым. Поэтому координаты точки
при котором суммарный расход в трубопроводах 2 и 3 равен расходу в трубопроводе 1, и является искомым. Поэтому координаты точки 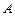 пересечения кривых 2+3 и 1 определяют решение задачи: ее абсцисса равна полному расходу
пересечения кривых 2+3 и 1 определяют решение задачи: ее абсцисса равна полному расходу 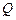 , а ордината - напору
, а ордината - напору 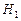 . Абсциссы точек
. Абсциссы точек 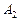 и
и 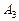 равны расходам
равны расходам 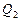 и
и 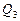 .
.
 2015-05-20
2015-05-20 1299
1299
