2015-05-20
3767
Существует большое количество алгоритмов расчета сетевых графиков как ручным, так и автоматизированным способом. Любой программный пакет по календарному планированию проекта (например, МS Рrоjесt, Тiте Linе, Spider, ОрепРLап, Рrimavera Suretrackи др.) позволяет рассчитать аналитические параметры любого сетевого графика. Но знание «ручных» технологий позволяет лучше понять взаимосвязь между этими показателями и использовать сетевые модели без каких-либо специализированных программ.
Итак, рассчитаем параметры сетевой модели табличным методом. Воспользуемся тем же сетевым графиком, на примере которого мы рассчитывали аналитические параметры в предыдущих параграфах (см. рисунок 28). Для этого воспользуемся таблицей 2.
Таблица 2 - Таблица для расчета аналитических параметров сетевой модели
| h-i | i | j |  |  |  |  | |  |  |  |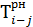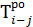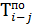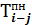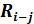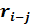
В графу 1 вносится количество работ, предшествующих рассчитываемой, в графу 2 — номера начальных событий рассчитываемых работ, в графу 3 — номера конечных событий рассчитываемых работ, в графу 4 — ранние начала работ, в графу 5 — продолжительности выполнения работ, в графу 6 — ранние окончания работ, в графу 7 — поздние окончания работ, в графу 8 — продолжительности выполнения работ, в графу 9 — поздние начала работ, в графу 10 — общие резервы работ, в графу 11 — частные резервы работ.
Графы 1, 2, 3, 5 и 8 заполняются данными из сетевого графика. Затем сверху вниз заполняются графы в таком порядке: 4 и 6, 7 и 9, 10, 11.
1. Определим 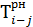и 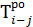для работ 0—1 и 0—2.
В графу 4 запишем нули, так как работы 0—1 и 0—2 выходят из исходного события графика. Графа 6 равняется сумме значений граф 4 и 5 (таблица 3).
Таблица 3 - Раннее начало и раннее окончание работ 0—1 и 0—2
| h-i | i | j | | | | | | | | |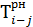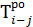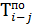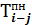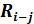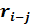
| - | ||||||||||
| - |
2. Определим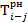 
и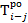 
для работ 1—2 и 1—3 (таблица 4).
Таблица 4 - Раннее начало и раннее окончание работ 1—2 и 1—3
| h-i | i | j | | | | | | | | |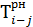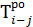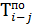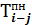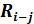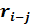
| - | ||||||||||
| - | ||||||||||
| 5 | ||||||||||
| 7 |
Значение графы 4 определяем следующим образом. В графе 1 по строке работы 1—2 проставлена цифра 1. Это означает, что работе 1—2 предшествует одна работа, т.е. если событие 1 искать сверху в графе 3, то оно встретится всего один раз. По строке найденного события (работа 0—1) отыскиваем значение графы 6, которое равно 2. Эту цифру переносим в графу 4 по строке работ 1—2 и 1—3 (так как обе работы выходят из одного и того же события и, следовательно, имеют одно и то же раннее начало), после этого определяем графу 6.
3. Определим 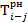и 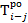для работ 2—3 и 2—4 (таблица 5).
Таблица 5 - Раннее начало и раннее окончание работ 2—3 и 2—4
| h-i | i | j | | | | | | | | |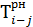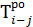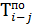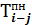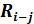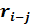
| - | ||||||||||
| - | ||||||||||
В графе 1 по строке работы 2—3 стоит цифра 2. Событие 2 встретится в графе 3 сверху от определяемой строки дважды. Событие 2 находится в строках работ 0—2 и 1—2. По этим строкам отыскиваем значения графы 6, они равны 6 и 5 соответственно.
Исходя из формулы (2) максимальное значение — 6 переносим в графу 4 по строкам работ 2—3 и 2—4.
4. Определим 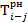и 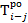для всех остальных работ аналогичным образом (таблица 6).
Таблица 6 - Раннее начало и раннее окончание всех работ
| h-i | i | j | | | | | | | | |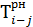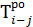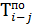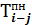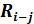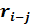
| - | ||||||||||
| - | ||||||||||
5. Для определения граф 7 и 9 нужно правильно заполнить еще одну — последнюю строку таблицы (таблица 7).
Таблица 7 - Таблица со строкой завершающего события
| h-i | i | j | | | | | | | | |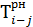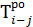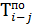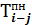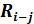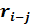
| - | ||||||||||
| - | ||||||||||
| — | — | - | — | — |
Как видим, в графе 3 стоит прочерк. Это означает, что в этой строке содержатся не параметры работы, а параметры события.
Известно, что событие не имеет продолжительности (прочерки в графах 5 и 8), а завершающее событие не имеет также и резервов (прочерки в графах 10 и 11). Следовательно, для завершающего события в графах 4, 6, 7 и 9 должна быть проставлена одна и та же величина — 24.
6. Определим 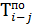и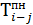 
для работ 4—5, 3—5, 3—4 и 2—4 (таблица 8).
Таблица 8 - Позднее окончание и позднее начало работ 4—5, 3—5, 3—4 и 2—4
| h-i | i | j | | | | | | | | |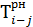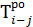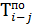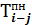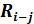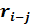
| - | ||||||||||
| - | ||||||||||
| — | — | - | — | — |
Расчет граф 7 и 9 осуществляется снизу вверх. Берем номер события из графы 3 (для работы 4—5 это будет событие 5). Затем отыскиваем это событие в графе 2 снизу от определяемой работы (4—5). По строке найденного события отыскиваем значение графы 9. Оно равно 24. Эту цифру записываем в графу 7 по строкам работ 4—5 и 3—5 (так как обе работы входят в одно и то же событие и, следовательно, имеют одну и ту же величину позднего окончания). После этого определяем значение графы 9 по работам 4—5 и 3—5, которое равно разнице значения графы 7 и значения графы 8.
7. Определим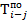 
и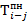 
для всех оставшихся работ (таблица 9).
Таблица 9 - Позднее окончание и позднее начало всех работ
| h-i | i | j | | | | | | | | |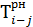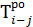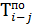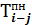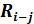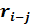
| - | ||||||||||
| - | ||||||||||
| — | — | - | — | — |
Находим событие 3 в графе 3 по строке работы 2—3. Затем отыскиваем это же событие внизу от определяемой работы (2—3) в графе 2. Здесь оно встречается дважды, в строках 3—4 и 3—5.
По строкам этих работ отыскиваем значение графы 9 и выбираем минимальное, которое и записываем в графу 7 по строкам работ 2—3 и 1—3.
Затем определяем значение графы 9. Аналогично определяются значения граф 7 и 9 и по всем остальным работам.
8. Определим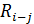 
для каждой работы.
Значения графы 10 получаются в результате вычитания по каждой строке значений графы 6 из значений графы 7. По строкам критических работ (0—2, 2—3, 3—5) в графе 10 записываются нули (таблица 10).
Таблица 10 - Полный резерв времени работ сетевого графика
| h-i | i | j | | | | | | | | |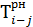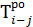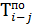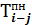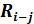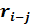
| - | ||||||||||
| - | ||||||||||
| — | — | - | — | — |
9. Определим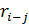 
для каждой работы.
Значение графы 11 рассчитывается как разность раннего начала (графа 4) и раннего окончания данной работы (графа 6). Работы, не имеющие общего резерва, не имеют и частного резерва, поэтому в графе 11 ставят 0 везде, где 0 имеется в графе 10 (таблица 11).
Таблица 11 - Частный резерв времени работ сетевого графика
| h-i | i | j | | | | | | | | |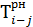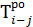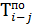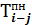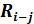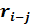
| - | ||||||||||
| - | ||||||||||
| — | — | - | — | — |
Частный резерв может быть найден и иным способом. У всех работ, обладающих нулевым полным резервом, частный резерв будет равен нулю. В нашем примере это работы 0—2, 2—3, 3—5. Таким образом, в графе 11 по строкам этих работ ставится 0. Затем находятся некритические работы, у которых конечное событие в графе 3 встречается один раз. По строкам этих работ в графе 11 ставится также 0. В нашем примере это будет работа 0—1. В строках работ, которые имеют завершающее событие в графе 3 более одного раза, в графе 11 ставится значение разницы между максимальным ранним окончанием этих работ и ранним окончанием данной работы. У работы, которая имеет максимальное раннее окончание, частный резерв будет равен 0. Так, в нашем примере событие 2 в графе 3 встречается дважды. По строкам этих событий отыскиваем значения графы 6. Они равны 6 и 5. По строке максимума, т.е. по строке работы 0—2, в графе 11 получаем 0, по строке работы 1—2 в графу 11 записываем результат разницы чисел 6 и 5, т.е. 1. Аналогично определяется графа 11 и по всем остальным строкам.
Приведем еще несколько примеров расчета несложных сетевых графикой табличным методом.
Пример 1. Рассчитаем сетевой график, представленный на рисунке
3 6
Аналитические параметры представим в таблице.
Расчет аналитических параметров сетевого графика
| h-i | i | j | | | | | | | | |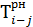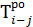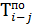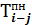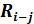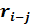
| - | ||||||||||
| - | - | - | - | - |
Критический путь сетевого графика проходит через события 0—1—2—4—5. Его длина составляет 16 дней.
Пример 2. Рассчитаем сетевой график, представленный на рисунке
7 1
2 3
| Пример 5.1. Рассчитаем сетевой график, представленный на рисунке. |
Расчет аналитических параметров сетевого графика
| h-i | i | j | | | | | | | | |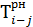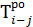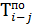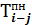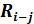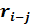
| - | ||||||||||
| - | ||||||||||
| - | - | - | - | - |
Критический путь сетевого графика проходит по событиям 0—1—2—3—4—5. Его длина составляет 20 дней.
Пример 3. Рассчитаем сетевой график, представленный на рисунке.
8
6 18
Аналитические параметры представленного сетевого графика приведем в таблице.
Расчет аналитических параметров сетевого графика
| h-i | i | j | | | | | | | | |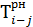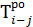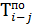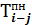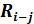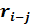
| - | ||||||||||
| - | - | - | - | - |
Аналитический путь данного сетевого графика проходит по событиям 1—2—3—6—7—8—9—11. Продолжительность критического пути составляет 39 дней.
Тесты и задания
Выберите один или несколько правильных ответов
1. График Гантта позволяет:
а) отразить продолжительность выполнения работ по проекту;
б) показать логическую связь между работами по проекту;
в) спрогнозировать ход выполнения работ по проекту.
2. В управлении проектом используются такие графы, как:
а) дерево целей;
б) дерево работ;
г) S-кривая;
д) сетевой график;
е) диаграмма Исикавы.
3. Ориентированный граф представляет собой:
а) граф, линии которого изображаются в виде направленных отрезков (стрелок);
б) граф, ребра которого не пересекаются;
в) граф, не имеющий в себе замкнутых контуров;
г) граф, вершины которого соединяются простыми (не направленными) отрезками.
4. Ориентированный граф состоит из:
а) вершин и дуг;
б) вершин и ребер;
в) структуры и поля.
5. Метод критического пути был впервые применен:
а) при организации военных поставок во время Второй мировой войны;
б) в программе Polaris;
в) при строительстве и обслуживании химических заводов фирмы DuPont.
6. Методы управления на основе сетевых моделей получили название:
а) методы обзора и пересмотра программ;
б) методы сетевого планирования и управления;
г) методы критического пути.
7. К недостаткам линейных моделей относятся:
а) сложность корректировки при изменении условий;
б) сложность вариантной проработки;
в) невозможность прогнозирования хода работ;
г) невозможность оптимизации запасов.
8. Работа — это:
а) трудовой процесс, требующий затрат времени и ресурсов;
б) совокупность операций, направленных на получение конкретного результата;
в) процесс, не требующий затрат труда, но требующий затрат времени.
9. Фиктивная работа — это:
а) трудовой процесс, не имеющий результатов;
б) неоплачиваемая работа;
в) работа, результаты которой никому не нужны;
г) зависимость между двумя или несколькими событиями, не требующая ни затрат времени, ни ресурсов, но показывающая логическую связь работ.
10. Ожидание — это:
а) технологическая или организационная взаимосвязь между событиями;
б) процесс, не требующий затрат труда, но требующий затрат времени;
в) вынужденный простой работников, машин и механизмов.
11. Событие — это:
а) результат выполнения одной или нескольких работ, позволяющий начинать следующую работу;
б) начало работы или завершение работы;
в) одновременное завершение или начало нескольких работ.
12. Событие совершается:
а) в течение максимальной продолжительности предшествующих работ;
б) в течение продолжительности предшествующей работы, деленной на десятичный логарифм продолжительности критического пути сетевого графика;
в) мгновенно и не имеет продолжительности.
13. Несколько работ входит:
а) в исходное событие;
б) в простое событие;
в) в сложное событие.
14. Путь — это:
а) продолжительность всех работ сетевого графика;
б) непрерывная последовательность работ, начиная от исходного события сетевой модели и заканчивая завершающим;
в) кратчайший маршрут от исходного события до завершающего.
15. Критический путь — это:
а) путь сетевого графика с кратчайшей длиной;
б) путь сетевого графика с максимальной длиной;
в) средняя арифметическая всех путей сетевого графика.
16. Упорядочение сетевого графика представляет собой:
а) ликвидацию излишних логических связей и событий, сокращение количества пересечений;
б) установление оптимального соотношения между количеством работ и количеством событий;
в) нумерацию событий.
17. Метод логического зонирования по слоям заключается:
а) в группировке работ по продолжительности;
б) группировке событий так, чтобы не было связей между событиями в одном слое;
в) группировке событий так, чтобы между слоями не было пересекающихся работ.
18. Коэффициент сложности — это:
а) отношение продолжительности критического пути к сумме продолжительностей всех работ;
б) отношение количества входящих работ в событие к количеству исходящих;
в) соотношение количества работ сетевого графика и количества событий.
19. Коэффициент сложности простых сетевых графиков равен:
а) 1;
б) 1,5;
в) 2.
20. Первую степень детализации имеют:
а) укрупненные сетевые графики для руководства компании;
б) сетевые графики по комплексам работ для руководителей отделов;
в) детализованные сетевые графики для оперативного управления.
21. Третью степень детализации имеют:
а) сетевые графики по комплексам работ для руководителей отделов;
б) детализированные сетевые графики для оперативного управления;
в) укрупненные сетевые графики для руководства компании.
22. «Сшивание» сетевых графиков представляет собой:
а) повышение уровня детализации сетевого графика;
б) объединении нескольких сетевых графиков в один;
в) снижение коэффициента сложности сетевого графика.
23. Граничными можно назвать:
а) завершающие события частных сетевых графиков;
б) общие события для объединяемых сетевых графиков;
в) события, имеющие не более одной входящей работы.
24. При построении сетевого графика, изображенного на рисунке, допущены следующие ошибки:
а) между событиями 1 и 5 неправильно изображены две параллельные работы;
б) между событиями 2 и 4 неправильно изображены две параллельные работы;
в) событие 3 — тупиковое.
25. При построении сетевого графика, изображенного на рисунке, допущены следующие ошибки:
а) между событиями 2 и 3 неправильно изображены две параллельные работы;
б) событие 5 тупиковое;
в) событие 4 тупиковое.
26. При построении сетевого графика, изображенного на рисунке, допущены следующие ошибки:
а) между событиями 2 и 5 неправильно изображены две параллельные работы;
б) событие 4 тупиковое;
в) событие 4 хвостовое.
27. При построении сетевого графика, изображенного на рисунке, допущены следующие ошибки:
а) событие 7 хвостовое;
б) события 2, 4, 6, 7, 8, 5 и 3 образуют цикл;
в) события 4, 8, 5 образуют цикл;
г) события 6, 7, 8, 5, 4 образуют цикл;
д) на графике изображено 3 цикла.
28. Правильно ли построен сетевой график, изображенный на рисунке?
а) сетевой график правильный;
Допущены следующие ошибки:
б) события 3, 5, 6 образуют цикл;
в) событие 3 хвостовое;
г) нарушена кодировка событий в работе 3—2;
д) события 5, 6, 7 образуют цикл.
29. При построении сетевого графика, изображенного на рисунке, допущены следующие ошибки:
а) между событиями 0 и 11 неправильно изображены параллельные работы;
б) события 1, 4, 6, 7, 8, 5, 2 образуют цикл;
в) нарушена кодировка событий в работе 2—1;
г) событие 3 — хвостовое;
д) на графике изображен один цикл;
е) на графике изображено два цикла;
ж) кодировка событий нарушена в шести работах;
з) кодировка событий нарушена в четырех работах.
30. Работы в и г могут начаться после выполнения работ а и б, выполняемых параллельно. Выберите правильный сетевой график.
31. Работа в может начаться после частичного выполнения работы а, а для полного завершения работы б необходимо полное выполнение работы а. Выберите правильный сетевой график.
а в а1 б а1 в
32. Работа г зависит от работы а, работа д зависит от а, б и в, а работа е зависит от а, б, г и д. Выберите правильный сетевой график.
а) а г б) а г
а г
в д
33. Даны работы а, б, в, г, д. Работу г можно начинать после окончания работ а и б, работу д — после окончания работ б и в. Выберите правильный сетевой график.
а) а г б) а г в) а г
в д в д в д
34. Даны работы а, б, в, г, д. Работы а и б начинаются одновременно, работы в и г — после работ а и б, работа д — после работ в и г. Выберите правильный сетевой график.
а) а в б) а
а в
35. Даны работы а, б, в, г, д. Работу г можно начинать по окончании работ а и в, работы д и в — по окончании работы б. Выберите правильный сетевой график.
а) б)
б в г б в д б в г
36. Рассчитайте табличным методом представленный сетевой график. Результаты занесите в приведенную ниже форму.
3 6
1 7
| i—j |  |  |  |  | | |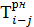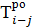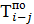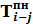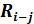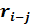
| 0—1 | ||||||
| 1—2 | ||||||
| 1—3 | ||||||
| 1—4 | ||||||
| 2—4 | ||||||
| 3—4 | ||||||
| 4—5 |
37. Рассчитайте табличным методом представленный сетевой график. Результаты занесите в приведенную ниже форму.
5
12 4 7
| i—j | | | | | | |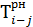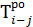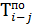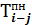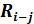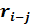
| 0—1 | ||||||
| 4—5 |
38. Рассчитайте табличным методом пре
