Лекция 2. Анализ цепей с экспоненциальным изменением сигналов

Экспоненциальным называется сигнал следующего вида:

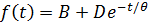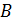, где и 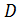некоторые константы, θ – постоянная времени цепи.

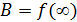при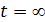

:

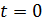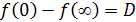
Тогда 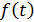равен: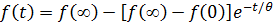

Рассмотрим два случая:

1. 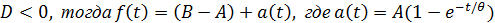экспоненциально возрастающий сигнал; (Рис. 2а)

2. 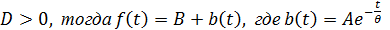экспоненциально спадающий сигнал. (Рис. 2б)

Рисунок 2. а) экспоненциально возрастающий сигнал; б) экспоненциально спадающий сигнал.

Произвольные графики получаются смещением приведенных графиков относительно оси 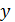(вверх или вниз).

Определим величины 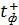и 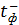. Из формулы 1 следует:

1.

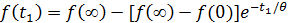
2.

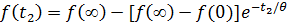
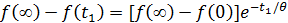
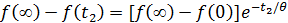
Поделим выражение 1 на выражение 2 и прологарифмируем:

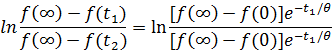
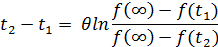
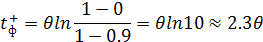
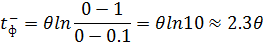
Определим вид цепей с экспоненциальным изменением сигнала. Экспоненциальный сигнал является решением следующего дифференциального уравнения первого порядка:

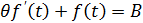
Этому уравнению отвечают токи и напряжения в RC и RL цепях. Сигнал на выходе анализируемой схемы является экспоненциальным только в том случае, если ее можно свести к одному из двух рассмотренных контуров, для этого должны соблюдаться следующие три условия:

1. Схема, как правило, должна содержать реактивности только одного типа (либо C, либо L);

2. При 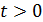входные токи и ЭДС не должны изменяться;

3. После окончания внешнего воздействия схема должна допускать сведение к пассивному RL или RC контуру.