Основные понятия: группа, подгруппа, группы подстановок n-ой степени, группы изометрий на плоскости.
Задание 1. Является ли группой множество G относительно заданной операции:
1) 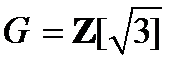 - множество чисел вида
- множество чисел вида 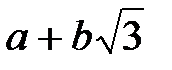 , где
, где 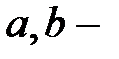 целые числа, относительно сложения;
целые числа, относительно сложения;
2) 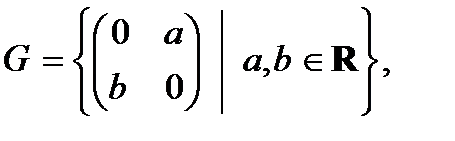 относительно сложения;
относительно сложения;
3) 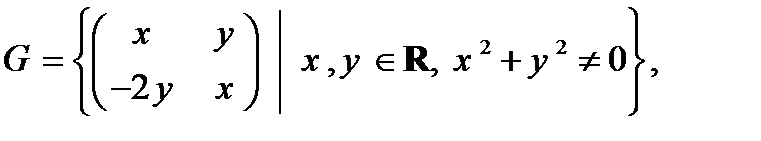 относительно умножения;
относительно умножения;
4) 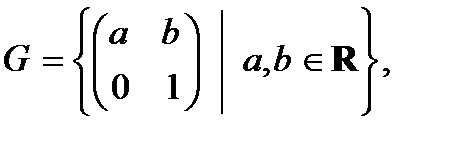 относительно умножения;
относительно умножения;
5) 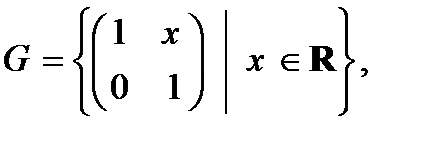 относительно умножения;
относительно умножения;
6) 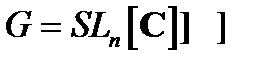 - множество матриц с определителем, равным 1, относительно умножения;
- множество матриц с определителем, равным 1, относительно умножения;
7) 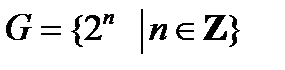 относительно умножения;
относительно умножения;
8) 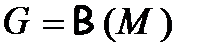 - множество всех подмножеств множества
- множество всех подмножеств множества 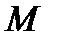 , относительно операции
, относительно операции  ;
;
9) 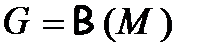 - - множество всех подмножеств множества
- - множество всех подмножеств множества 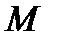 , относительно операции
, относительно операции  ;
;
10) 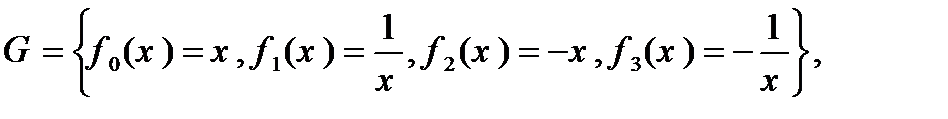 относительно композиции;
относительно композиции;
11) 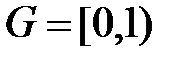 относительно операции
относительно операции  , где
, где 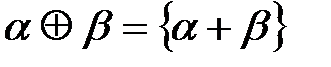 - дробная часть числа;
- дробная часть числа;
12) 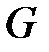 - множество функций вида
- множество функций вида 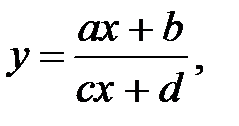 где
где 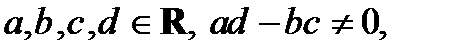 относительно композиции функций
относительно композиции функций
13) 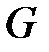 - множество всех вещественных чисел относительно операции
- множество всех вещественных чисел относительно операции  :
: 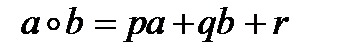 , где
, где 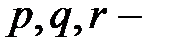 фиксированные действительные числа;
фиксированные действительные числа;
14) 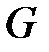 - множество верхних нильтреугольных матриц относительно операции
- множество верхних нильтреугольных матриц относительно операции 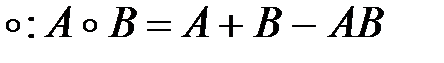 ;
;
15) 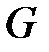 - множество верхних нильтреугольных матриц порядка 3 относительно операции
- множество верхних нильтреугольных матриц порядка 3 относительно операции 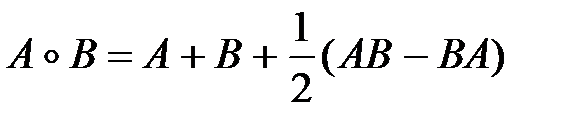 ;
;
Задание 2. Является ли множество H подгруппой группы G:
1) H =  , G =
, G = 
2) H = 3  , G =
, G = 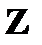
3) H = 5  , G =
, G = 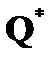
4) H = 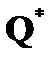 , G =
, G = 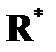
5) H = 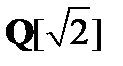 , G =
, G = 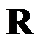
6) H = {-1,1}, G = 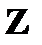
7) 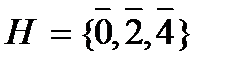 , G =
, G = 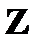 6
6
8) 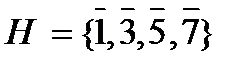 , G =
, G = 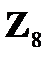
9) H = 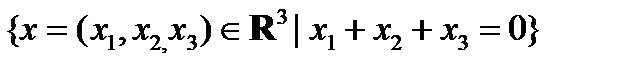 , G =
, G = 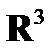
10) H = 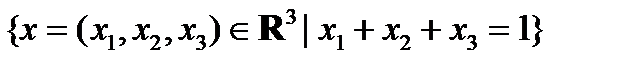 , G =
, G = 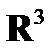
11) H = 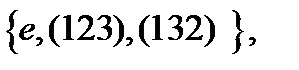 G =
G = 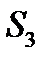
12) H = 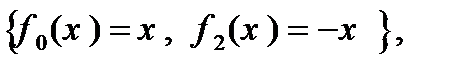
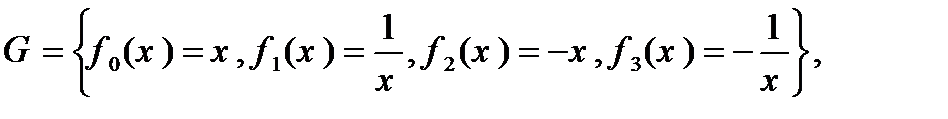
Задание 3. Вычислить 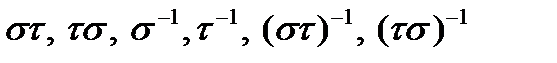 если
если
1) 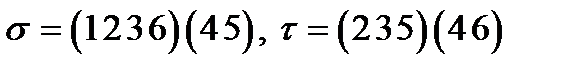
2) 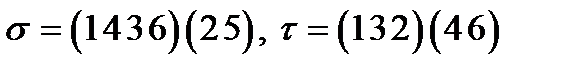
3) 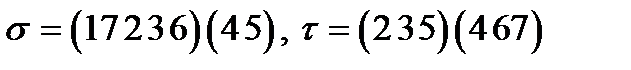
4) 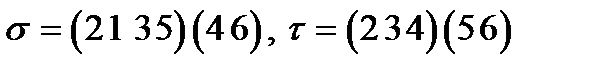
5) 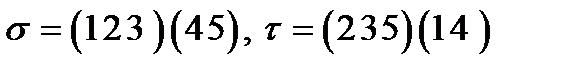
6) 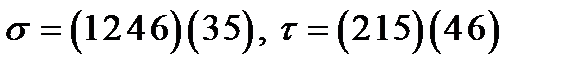
7) 
8) 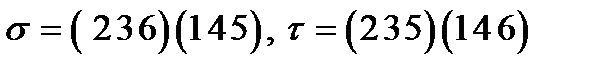
9) 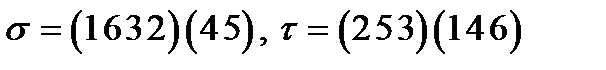
10) 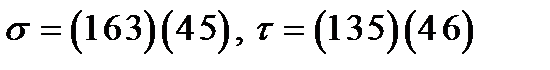
11) 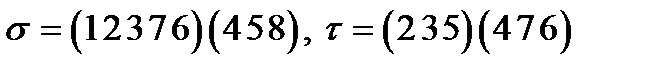
12) 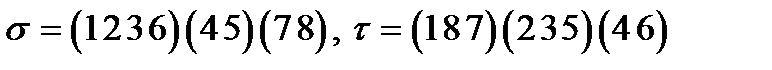
Задание 4. Выписать группу изометрий следующих плоских фигур:
1) равнобокая трапеция;
2) параллелограмм;
3) прямоугольник;
4) буква Х;
5) эллипс;
6) гипербола;
7) кубическая парабола;
8) пятиконечная звезда;
9) шестиконечная звезда;
10) буква Ж;
11) график уравнения 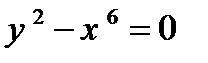 ;
;
12) лемниската Бернулли.
 2015-05-10
2015-05-10 736
736






