Теоретическая справка. Цель работы: приобретение навыков решения краевых задач для однородно-эллиптического дифференциального уравнения в частных производных второго порядка на

Лабораторная работа № 3

Цель работы: приобретение навыков решения краевых задач для однородно-эллиптического дифференциального уравнения в частных производных второго порядка на непрямоугольной области с помощью вариационных методов Ритца и наименьших квадратов.

Задание на работу: получить самостоятельно приближенное решение однородно-эллиптического уравнения:

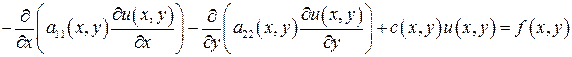
на непрямоугольной области при смешанных однородных граничных условиях с помощью вариационных методов Ритца и наименьших квадратов. При этом на разных отрезках границы 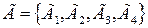заданы свои граничные условия.

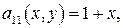
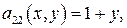
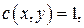
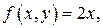
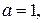
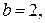
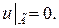
Теоретическая справка

Преобразуем исходную область – четырехугольник с вершинами в точках с координатами: 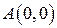, , 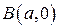, 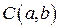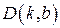в прямоугольную, с вершинами в точках с координатами , , , .

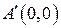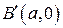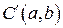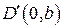Для этого необходимо сделать замену переменных, в которой

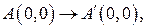
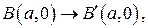
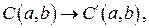
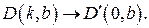
где 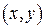– координаты точек исходной области, 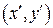– координаты точек прямоугольной области.

Для решения поставленной задачи воспользуемся формулой билинейного преобразования:

(*)

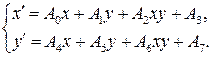Подставим в формулу (*) соответствующие координаты точек.

Получим систему из 8 уравнений с 8 неизвестными коэффициентами :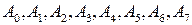

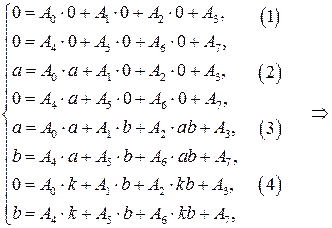
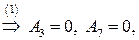
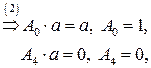
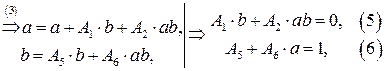
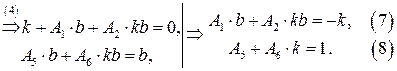
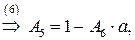
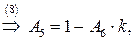
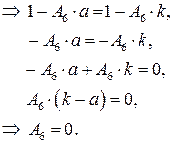
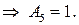
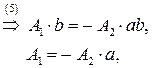
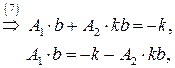
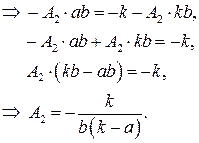
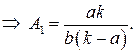
Подставляя найденные значения в систему (*), получаем преобразование координат, переводящее заданную область в прямоугольную:

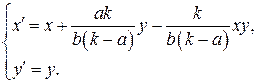
Проверка:

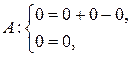– верно,

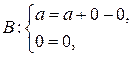– верно,

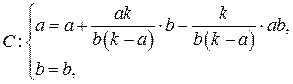– верно,

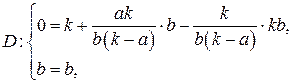
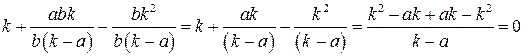– верно.

Для решения поставленной задачи также можно воспользоваться формулой проективного преобразования:

(**)

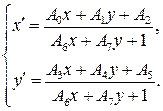Подставим в формулу (**) соответствующие координаты точек.

Получим систему из 8 уравнений с 8 неизвестными коэффициентами :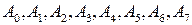

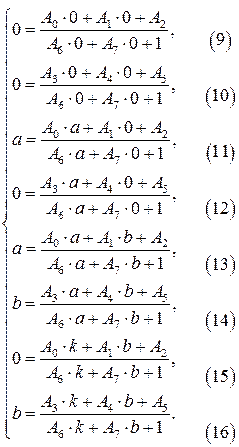
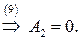
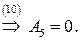
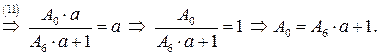
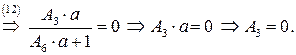
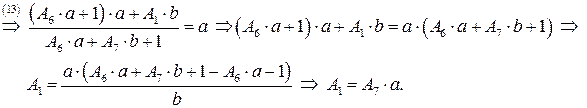
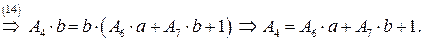
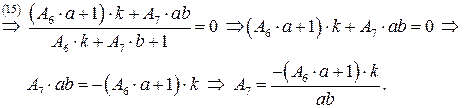
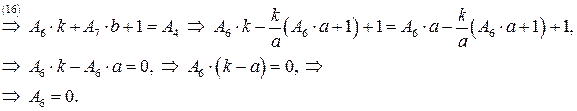
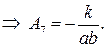
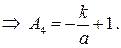
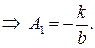
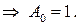
Подставляя найденные значения в систему (**), получаем преобразование координат, переводящее заданную область в прямоугольную:

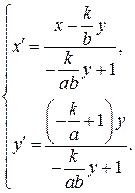
Упростим полученные выражения:

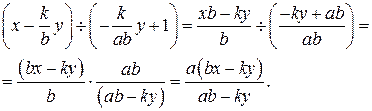
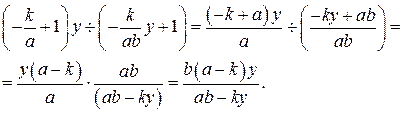
Окончательно получаем:

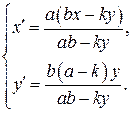
Проверка:

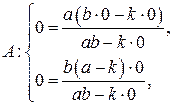– верно,

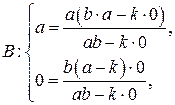– верно,

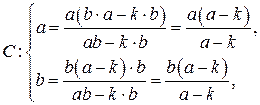– верно,

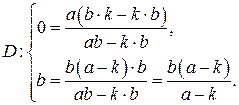– верно.

Вывод: таким образом, исходную область можно преобразовать в прямоугольную с помощью следующих преобразований:

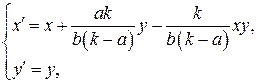
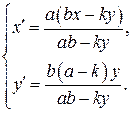
БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Гаев А.В., Скобельцын С.А. Вариационные методы решения краевых задач. – Тула: Изд-во ТулГУ, 2009. – 192с.
2. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. - СПб: Изд-во «Лань», 2008. – 368с.
3. Фадеев М.А., Марков К.А. Основные методы вычислительной математики. – СПб: Изд-во «Лань», 2008. – 160с.
4. Бенерджи П., Баттерфилд Р. Методы граничных элементов в прикладных науках.- М.: Мир, 1984.- 494с.
5. Галлагер Р. Метод конечных элементов. Основы.- М.:Мир, 1984.- 428с.
6. Михлин С.Г. Вариационные методы в математической физике. М.: Наука, 1970. - 512с.
7. Михлин С.Г. Численная реализация вариационных методов. М.: Наука, 1966. - 450с.
8. Норри Д., Фриз Ж. Введение в метод конечных элементов.- М.: Мир, 1981.- 304с.
9. Партон В.З., Перлин П.И. Методы математической теории упругости. М.: Наука, 1981.- 688 с.
10. Ректорис К. Вариационные методы в математической физике и технике. - М.: Мир, 1985.- 590 с.