Тема: Параметрические критерии различия
1. t -критерий Стьюдента Рассмотрим пример использования /-критерия Стьюдента для несвязных и неравных по численности выборок
Задача. Психолог измерял время сложной сенсомоторной реакции выбора (в мс) в контрольной и экспериментальной группах В экспериментальную группу (X) входили 9 спортсменов высокой квалификации Контрольной группой (Y) являлись 8 человек, активно не занимающиеся спортом Психолог проверяет гипотезу о том, что средняя скорость сложной сенсомоторной реакции выбора у спортсменов выше, чем эта же величина у людей, не занимающихся спортом
Решение. Результаты эксперимента представим в виде таблицы 1, в которой произведем ряд необходимых расчетов.
Таблица 1
| № | Группы | Отклонения от среднего | Квадраты отклонений | |||
| X | Y | х-хср | y-yср | 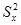 для х для х
| 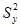 для y для y
| |
| - 22 | - 58 | |||||
| - 106 | ||||||
| - 17 | ||||||
| - 2 | ||||||
| - 77 | ||||||
| -36 | ||||||
| - 8 | ||||||
| - | -56 | - | - | |||
| Сумма | ||||||
| Среднее |
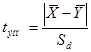 , где
, где 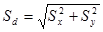
Число степеней свободы k = (n 1-1+(n 2-1)=9 + 8- 2 = 15.
По таблице 16 Приложения 1 для данного числа степеней свободы находим t табл и строим ось значимости:
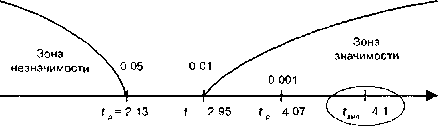
Справочная информация по технологии работы в Excel. Выбираем менюСервис -> Анализ данных -> «Двухвыборочный t -тест с одинаковыми дисперсиями»и «Двухвыборочный t –тест с различными дисперсиями» дляпроверки гипотез о различии между средними (математическими ожиданиями) двух нормальных распределений соответственно с неизвестными, но равными дисперсиями и с неизвестными дисперсиями, равенство которых не предполагается.
| X | Y | ||||||
| Двухвыборочный t-тест с одинаковыми дисперсиями | |||||||
| X | Y | ||||||
| Среднее | |||||||
| Дисперсия | 2596,285714 | ||||||
| Наблюдения | |||||||
| Объединенная дисперсия | 3120,4 | ||||||
| Гипотетическая разность средних | |||||||
| - | df | ||||||
| t-статистика | -4,126241812 | ||||||
| P(T<=t) одностороннее | 0,000448628 | ||||||
| t критическое одностороннее | 1,753050356 | ||||||
| P(T<=t) двухстороннее | 0,000897256 | ||||||
| t критическое двухстороннее | 2,131449546 |
 2015-05-10
2015-05-10 345
345






